3)
0 £ x £ a,
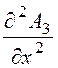 = -ma·d2, А3 = -
= -ma·d2, А3 = -![]() d2·х2
+ С5·х + С6,
d2·х2
+ С5·х + С6,
4)
x > a, 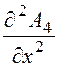 = 0, А4 = С7·х
+ С8.
= 0, А4 = С7·х
+ С8.
3. Полученных уравнений недостаточно для определения
постоянных интегрирования С1÷С8, поэтому
получим формулы для напряженности магнитного поля. Векторный потенциал с
напряжённостью связан следующим образом: rot![]() =
= ![]() = ma·
= ma·![]() .
.
Но согласно табл. 11.1
rot![]() =
=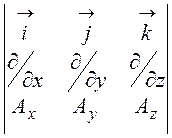 =
=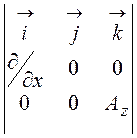 = -
= -![]()
![]() .
.
Тогда ![]() = -
= -![]()
![]()
![]() и
H = -
и
H = -![]()
![]() .
.
Таким образом,
H1 = -![]() ;
H2 = d1·х
–
;
H2 = d1·х
–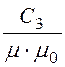 ; H3 = d2·х –
; H3 = d2·х –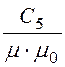 ;
H4 = -
;
H4 = -![]() .
.
4. Составим и решим уравнения для нахождения постоянных интегрирования.
При x = -a
в соответствии с законом полного тока (H-а·2·50а = -I – знак
«минус», так как с левой стороны шины напряжённость направлена против оси у):
H1(x
= -a) = -I/(100a)
= -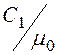 ,
,
откуда С1 =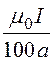 =
=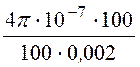 =
6,283·10-4.
=
6,283·10-4.
При x = -a в соответствии с граничным условием H1t = H2t
H1(x = -а) = H2(x = -а) или -С1/m0 = d1·(-а) – С3/(mm0); откуда
С3 = d1·(-а)·mm0 + С1·m = -375000·0,002·6·4p ·10-7 + 6,283·10-4·6 = -1,885·10-3.
При x = 0 H2(x= 0) = H3(x= 0) или С3 = С5.
При x = a H3(x = а) = H4(x = а) или d2·а – С5/(mm0) = -С7/m0; откуда
С7 = -d2·а·m0 + С5/m = -125000·0,002·4p ·10-7 + (-1,885·10-3)/6 = -6,283·10-4.
Примем, что при x = 0 А2(x = 0) = А3(x = 0) = 0, тогда С4 = С6 = 0.
При x = -a А1(x = -а) = А2(x = -а) или
С1·(-а) + С2 = -½mаd1·(-а)2 + С3·(-а) + С4, откуда
С2 = -½mаd1·(-а)2 + С3·(-а) + С4 – С1·(-а) = -½·6·4p ·10-7·375000·0,0022 +
+ 1,885·10-3·0,002 + 0 + 6,283·10-4·0,002 = -6,283·10 -7.
При x = a А3(x = а) = А4(x = а) или -½mаd2·а2 + С5·а + С6 = С7·а + С8, откуда С8 = -½mаd2·а2 + С5·а + С6 – С7·а = -½·6·4p ·10-7·125000·0,0022 –
– 1,885·10-3·0,002 + 0 + 6,283·10-4·0,002 = -4,398·10 -6.
5. Окончательно получаем:
А(х)
=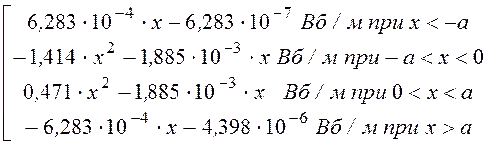 ,
,
Н(х) = 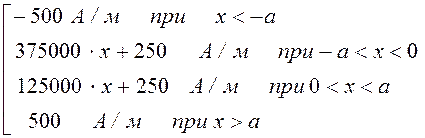 .
.
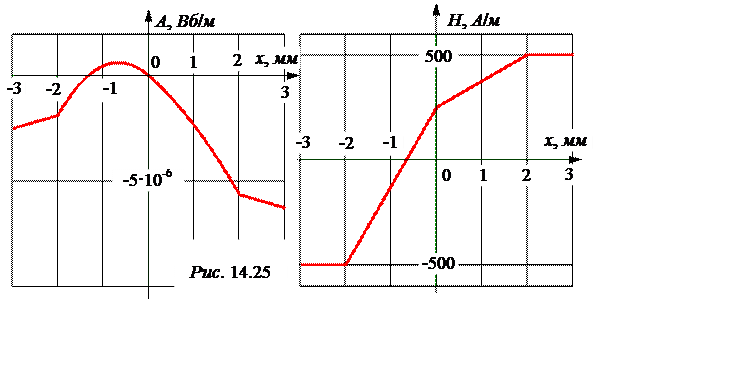
По этим формулам построены графики А(х) и Н(х), которые представлены на рис. 14.25.
 |
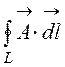 . В качестве контура интегрирования возьмём
прямоугольник 0-1-2-3-0 длиной 1м (рис. 14.24,б). Причём вдоль сторон
0-1 и 2-3 интеграл равен нулю, так как на этих участках угол между
. В качестве контура интегрирования возьмём
прямоугольник 0-1-2-3-0 длиной 1м (рис. 14.24,б). Причём вдоль сторон
0-1 и 2-3 интеграл равен нулю, так как на этих участках угол между 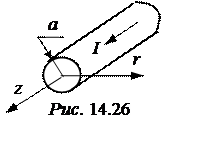 Ф =
Ф =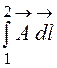 =
А(х = -а)·1м = -1,885·10-6 Вб.
=
А(х = -а)·1м = -1,885·10-6 Вб.
Знак «минус» в ответе для магнитного потока означает, что магнитный поток направлен против поло-жительной нормали к контуру2), то есть снизу вверх.
ЗАДАЧА 14.22. Постоянный ток I = 350 А замыкается по металли-ческой цилиндрической шине радиусом а = 20 см (рис. 14.26). Шина изго-товлена из материала с относительной магнитной проницаемостью m = 4 и находится в воздухе. Построить графики зависимости векторного магнитного потенциала и напряжённости магнитного поля в функции координат.
Решение
Порядок действий тот же, что и при решении задачи 14.21.
1. Плотность тока в шине d = I/(pа2) = 2785 А/м2.
2. Векторный магнитный потенциал имеет только одну
составляющую, направленную параллельно оси z, и зависит
только от координаты r. При этих условиях уравнение Пуассона в
цилиндрической системе координат принимает вид: Ñ 2А =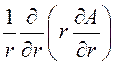 =
=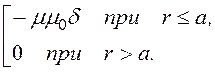
Его решение А1 = - ¼mm0d r2 + С1ln(r) + C2, А2 = С3ln(r) + C4.
Чтобы при r = 0 А1 не принимало бесконечных значений, слагаемое С1ln(r) должно отсутствовать, то есть С1 = 0. Кроме того, пусть А1 = 0 при r = 0, тогда C2 = 0 и А1 = - ¼mm0dr 2.
3. Напряжённость магнитного поля ![]() = rot
= rot![]() /ma =
-
/ma =
-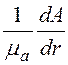 .
.
Таким образом, Н1 = ½dr –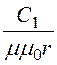 = ½dr; Н2 = -
= ½dr; Н2 = -![]() .
.
4. При r = а Н1 = Н2, откуда С3 = - ½m0dа2 = -7·10-5,
А1 = А2, откуда С4 = - ¼mm0dа2 – С3ln(а) = -25,26·10-5.
5. Окончательно получаем
А(r) =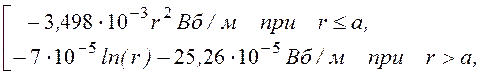
Н(r) =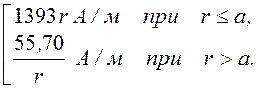
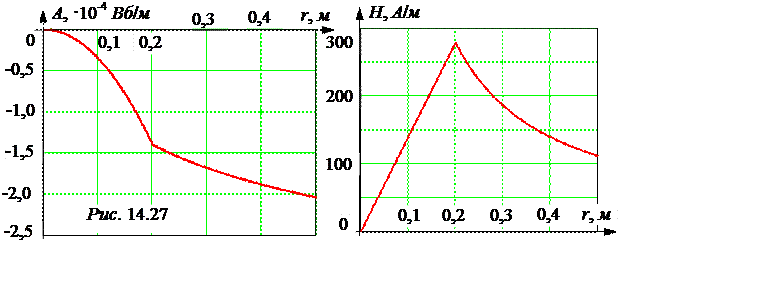 Построенные по этим формулам графики А(r) и Н(r) представлены на рис. 14.27.
Построенные по этим формулам графики А(r) и Н(r) представлены на рис. 14.27.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.