Министерство образования Республики Беларусь
Учреждение образования «Гомельский государственный технический университет имени П. О. Сухого»
Кафедра «Высшая математика»
Л.Д. Корсун, С.П. Курлович, Е.Б. Чуркин
Линейная алгебра и аналитическая геометрия
ПРАКТИЧЕСКОЕ пособие к домашним заданиям курса «Высшая математика» для студентов дневного отделения
Гомель 2003
УДК 662.61
Л65
Линейная алгебра и аналитическая геометрия: Практическое пособие к домашним заданиям курса «Высшая математика» для студентов дневного отделения. – ГГТУ им. П.О. Сухого, 2003. – 60 с.
Материал практического пособия содержит основные разделы программы «Линейная алгебра и аналитическая геометрия». Наряду с кратко изложенной теорией, практическое пособие содержит решенные примеры и достаточное количество заданий для домашней работы. Для студентов дневного отделения.
Рецензент: к.ф.-м.н., доцент кафедры «Высшая математика» ГГТУ им. П.О. Сухого Вальковская В.И.
ISBN 985-420-249-6
© Учреждение образования «Гомельский государственный технический университет имени П. О. Сухого», 2003
Матрицей размера ![]() называется таблица вещественных чисел вида:
называется таблица вещественных чисел вида:
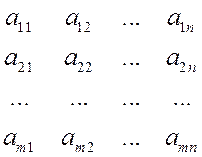 .
.
Матрицы обозначаются: ![]() , А,
, А,
![]() ,
,
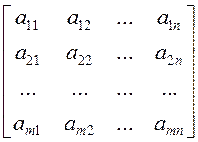 ,
, 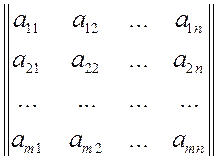 ,
, 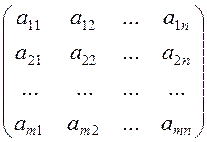 , где
, где ![]() –
элемент матрицы;
–
элемент матрицы; ![]() – i-я строка;
– i-я строка; ![]() – j-й столбец. Столбцы и строки
называются рядами.
– j-й столбец. Столбцы и строки
называются рядами.
Различают следующие матрицы:
·
Квадратные матрицы – число строк совпадает с числом столбцов ![]() , где
, где ![]() –
порядок матрицы
–
порядок матрицы
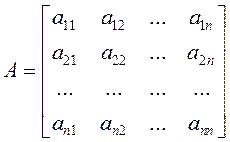 .
.
В квадратной матрице элементы ![]() образуют
главную диагональ, а элементы
образуют
главную диагональ, а элементы ![]() – побочную диагональ.
– побочную диагональ.
·
Нулевые матрицы – все элементы равны нулю ![]() .
.
· Диагональные матрицы (А) – все элементы равны 0 кроме элементов стоящих на главной диагонали. Диагональная матрица, у которой элементы главной диагонали равны 1, называется единичной матрицей (Е).
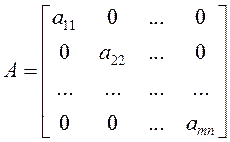 ,
, 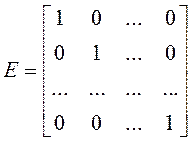 .
.
Суммой (разностью) матриц ![]() и
и ![]() называется
матрица
называется
матрица ![]() , такая, что
, такая, что ![]() , где i
= 1, 2, …, n, j = 1, 2, …, m.
, где i
= 1, 2, …, n, j = 1, 2, …, m.
Пример 1.
Найти сумму А + В матриц 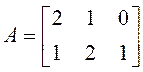 ,
, 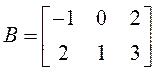 .
.
Решение. 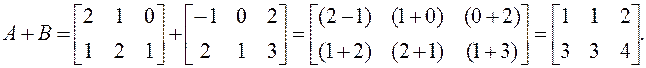
Произведением матрицы ![]() на число
на число ![]() называется
матрица
называется
матрица ![]() , элементы которой
, элементы которой ![]() (все
элементы матрицы А умножаются на
(все
элементы матрицы А умножаются на ![]() ).
).
Произведением матриц ![]() и
и ![]() называется
матрица
называется
матрица ![]()
![]() , элементы которой
, элементы которой 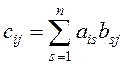 (i
= 1, 2, …, m, j = 1, 2, …, k).
(i
= 1, 2, …, m, j = 1, 2, …, k).
Пример 2. Найти
произведение АВ матриц 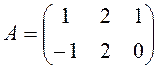 ,
, 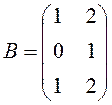 .
.
Решение. 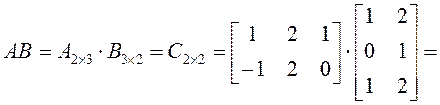
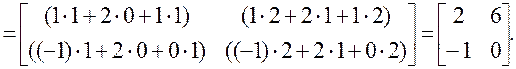
Транспонированием матрицы
![]() называется матрица
называется матрица ![]() ,
каждая строка которой есть соответствующий столбец матрицы А (производится замена
строк столбцами).
,
каждая строка которой есть соответствующий столбец матрицы А (производится замена
строк столбцами).
Пример 3. Найти 3ВТ,
где 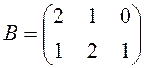 .
.
Решение. 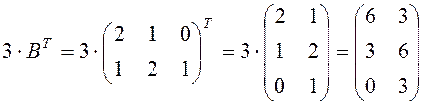 .
.
ЗАДАНИЯ
|
1.
Найти
3. Найти А+В
5. Найти 2А-3В
7. Найти 3А-ВТ
9. Найти 3А-2АТ+4Е
11. Найти А·В
|
2.
Найти
4. Найти А-В
6. Найти 2А-3В
8. Найти 4А-2ВТ
10. Найти 4А+3АТ-2Е
12. Найти А·В
|
В задачах 13-16 найти А·В и В·А
13. 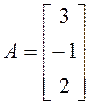 ,
, ![]() . 14.
. 14. 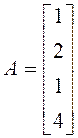 ,
, ![]() .
.
15. 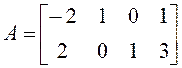 ,
, 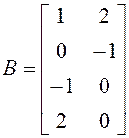 . 16.
. 16. 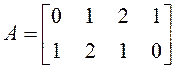 ,
, 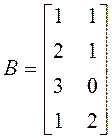 .
.
17. Найти
АВС 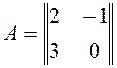 ,
, 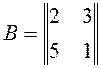 ,
, 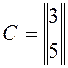 .
.
18. Найти
АВС 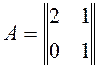 ,
, 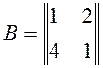 ,
, 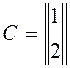 .
.
19. Найти
А2, если 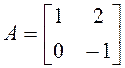 . 20.
Найти А2, если
. 20.
Найти А2, если 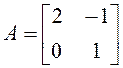 .
.
21.
Проверить равенство ![]() ,
,
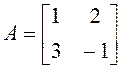 ,
, 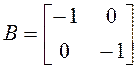 .
.
22.
Проверить равенство ![]() ,
,
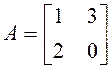 ,
, 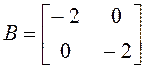 .
.
23. Найти
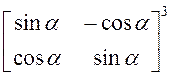 . 24. Найти
. 24. Найти 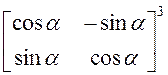 .
.
25. Найти
А, если 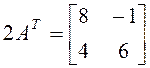 .
.
26. Найти
В, если 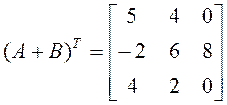 ,
, 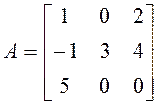 .
.
27. Найти
(АВ)Т, если 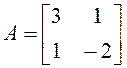 ,
, 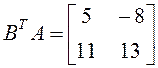 .
.
28. Найти ВА, если 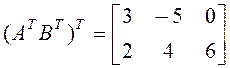 .
.
Перестановкой из n натуральных чисел 1,
2, 3, …, n называется любое их расположение. Перестановка обозначается ![]() .
.
Пример-пояснение. (1, 4, 3, 2, 5) и (2, 1, 5, 3, 4) – две перестановки из чисел 1, 2, 3, 4, 5.
Из чисел 1, 2, 3, …, n возможно n! перестановок.
Пример-пояснение. Из чисел 1, 2, 3 возможно 3! =1·2·3 = 6 перестановок:
(1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1).
Если в перестановке большее число стоит перед меньшим, то
два числа образуют инверсию. Число инверсий в перестановке ![]() обозначаем
обозначаем
![]() .
Если число инверсий в перестановке четное (нечетное), то перестановка четная
(нечетная).
.
Если число инверсий в перестановке четное (нечетное), то перестановка четная
(нечетная).
Пример
1. Найти число инверсий в
перестановке (5, 3, 2, 4, 1), ![]()
Решение. Число 5 больше 3, 2, 4, 1 и, следовательно,
образует четыре инверсии; следующее число 3 больше 2 и 1 и, следовательно,
образует две инверсии и т. д., поэтому общее число инверсий ![]() .
.
Определителем квадратной матрицы ![]() называется сумма n!
слагаемых вида
называется сумма n!
слагаемых вида ![]() и обозначается
и обозначается
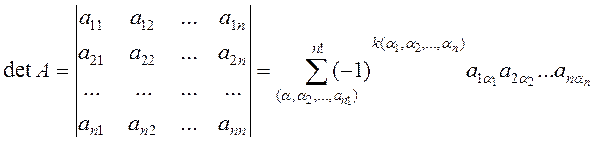 .
.
Выражение ![]() – произведение n сомножителей, взятых по одному из каждого столбца и
строки.
– произведение n сомножителей, взятых по одному из каждого столбца и
строки.
Из определения определителя следуют следующие его свойства:
1. ![]() . Определители матрицы А и
транспонированной АТ равны.
. Определители матрицы А и
транспонированной АТ равны.
2. Если все элементы некоторого ряда определителя равны нулю, то определитель равен нулю.
3. Если все элементы некоторого ряда имеют общий множитель, то его можно вынести за знак определителя.
4. При перестановке двух параллельных рядов определитель меняет знак на противоположный.
5. Если два параллельных ряда определителя пропорциональны, то определитель равен 0.
6. Если некоторый ряд определителя разбить на сумму двух слагаемых, то определитель равен сумме двух определителей. Первый определитель содержит в этом ряду первые слагаемые, а второй определитель в этом ряду содержит вторые слагаемые; остальные ряды, параллельные указанному, у всех определителей одинаковы.
Пример-пояснение. 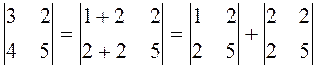 .
.
7. Если матрица В получена из матрицы А прибавлением
к некоторому ряду другого параллельного ряда, умноженного на произвольное число
λ, то ![]() .
.
Исходя из определения определителя, получают правила вычисления определителя 1го, 2го, 3го порядка.
I. Определитель
матрицы первого порядка: ![]() .
.
Пример-пояснение. ![]() .
.
II. Определитель второго порядка:
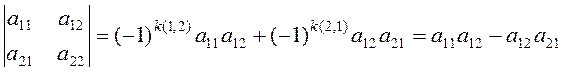 , т.е. равен произведению
элементов главной диагонали минус произведение элементов побочной диагонали.
, т.е. равен произведению
элементов главной диагонали минус произведение элементов побочной диагонали.
Пример-пояснение. 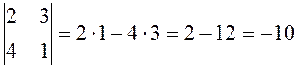 .
.
III. Определитель третьего порядка:
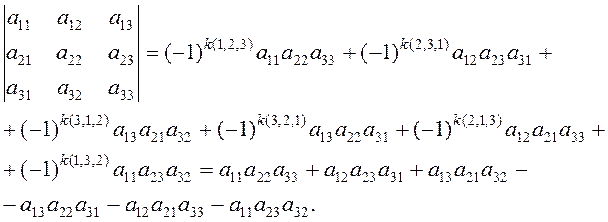

+ –
Рис. 1. Правило треугольника
Пример-пояснение. 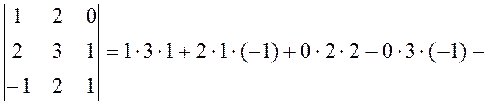
![]() .
.
Определители 4-го и старших порядков вычисляются путем приведения их к треугольному виду, используя свойства определителя.
Пример 2. Вычислить определитель 3-го порядка, используя свойства:
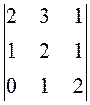 .
.
Решение
|
|
Получим единицу в левом верхнем углу определителя. Для этого поменяем 1 и 2 строчки (получить 1 всегда возможно, используя свойство определителя). Далее приводим определитель к верхнетреугольному виду (получаем нули ниже главной диагонали). Для этого умножим первую строку на –2 и прибавим ко второй. Сумму запишем вместо второй строки (см. св-во 7). Далее к третьей строке прибавим вторую. Получили определитель треугольного вида, который равен произведению диагональных элементов. |
ЗАДАНИЯ
|
Найти число инверсий в перестановке. |
|
|
29. (1, 5, 7, 4, 2, 3, 6). 31. (1, 2, 11, 7, 6, 5, 3, 9, 10, 4, 8). 33. (1, 3, 5, 7,…, (2n-1), 2, 4, 6, 8,…, 2n). |
30. (2, 3, 1, 4, 5). 32. (13, 8, 7, 1, 3, 2, 5, 4, 6, 11, 12, 10, 9). 34. (2, 4, 6,…, 2n, 1, 3, 5,…, 2n-1). |
Вычислить.
35. ![]() ,
, 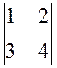 ,
, 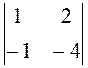 . 36.
. 36.
![]() ,
, 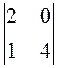 ,
, 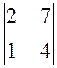 . 37.
. 37. 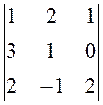 .
.
38. 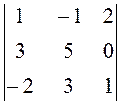 . 39.
. 39. 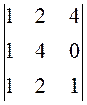 . 40.
. 40. 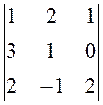 .
.
Вычислить определитель, используя свойства.
41. 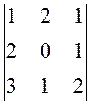 . 42.
. 42. 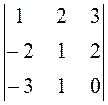 . 43.
. 43.
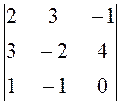 . 44.
. 44. 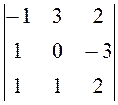 .
.
45. 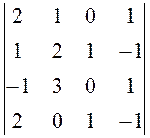 . 46.
. 46. 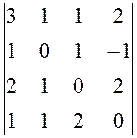 . 47.
. 47. 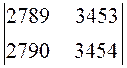 . 48.
. 48.
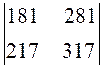 .
.
Выберем в матрице А s строк и s столбцов.
Минором М порядка s матрицы А называется определитель, составленный из элементов, стоящих на пересечении выбранных s строк и s столбцов.
Дополнительным
минором ![]() ,
к минору М порядка s, называется определитель, составленный из
элементов, оставшихся после вычеркивания тех s строк и s столбцов
квадратной матрицы А, которые составили минор М.
,
к минору М порядка s, называется определитель, составленный из
элементов, оставшихся после вычеркивания тех s строк и s столбцов
квадратной матрицы А, которые составили минор М.
Алгебраическим дополнением минора М называется дополнительный к нему минор, умноженный на (-1)σ, где σ – сумма
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.