Построение многоугольников и многогранников, страница 2

Point *p;                                 // массив вершин

public:

int isin(Point t);            // тест на принадлежность

};

// реализация алгоритма

int Polygon::isin(Point t)

{

int i, parity = 0;

for(i = 0; i < n; i++)

if(intersect(t,

p[i], p[(I + 1)%n]))

parity = 1 - parity;

return parity;

}

Примеры использования теста на принадлежность будут даны позже.

Если включить в цикл действия, которые выполняет функция intersect(), в подпрограмму isin(), то получим следующий текст подпрограммы проверки на принадлежность точки многоугольнику:

int Polygon::isin(Pnt t)

{

int i,j, parity = 0;

for(i = 0, j = n-1; i < n; j = i++)

{

if (( ( (p[i].y<=t.y)&&(t.y<p[j].y) )||

((p[j].y<=t.y)&&(t.y<p[i].y)))&&

(t.x<(p[j].x-p[i].x)*(t.y-p[i].y)/

(p[j].y-p[i].y)+p[i].x))

parity=1-parity;

}

return parity;

}

В случае, когда многоугольник не является простым, этот тест не всегда дает желаемый результат.

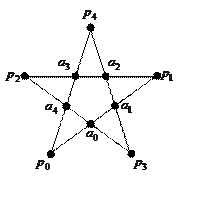
Рис. 6.2. Точки многоугольника a₀a₁a₂a₃a₄ являются внешними

Например, точки внутреннего выпуклого многоугольника a₀a₁a₂a₃a₄ (рис. 6.2) всегда будут внешними по отношению к многоугольнику p₀p₁p₂p₃p₄, хотя в некоторых случаях их удобно считать внутренними. В этих случаях можно применить алгоритм, описанный ниже.

Тест на принадлежность методом углов. Задан многоугольник, состоящий из вершин p₀, p₁,…,p_n-1, и точка t. В этом алгоритме проверки на принадлежность точки t многоугольнику, точка t берется за начало новой системы координат. В результате вся плоскость будет разбита на 4 области–квадраты относительно начала координат t.

Пусть c_i = code (p_i)  {0, 1, 2, 3} обозначает четверть, содержащую точку p_i. Введем число, характеризующее изменение номера четверти при переходе от точки p_i к точке p_i+1. Если i + 1 = n, то вместо p_i+1 берется точка p₀. Положим:

                  0, если c_i = c_i+1,

1, если c_i+1 = (c_i + 1) mod 4

m_i =          – 1, если c_i+1 = (c_i – 1) mod 4,

± 2, если c_i+1 = (c_i + 2) mod 4.

В последнем случае если t находится слева от направленного отрезка p_ip_i+1, то m_i = + 2, а если справа, то m_i = – 2. Индексом ind_iP точки t относительно многоугольника P называется число .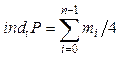

Теорема. Индекс ind_iP равен 0 тогда и только тогда, когда точка t расположена вне многоугольника P.

Пример. Рассмотрим точку t и многоугольник, изображенные на рис. 6.3. Точки p первой четверти имеют код code (p) = 0, второй — code (p) = 1, третьей — code (p) = 2, четвертой — code (p) = 3.

Рис. 6.3. Вычисление индекса точки t

Получаем m₀ = 2, m₁ = 0, m₂ = 1, m₃ = 1, m₄ = – 2, m₅ = – 2, следовательно, индекс равен:

ind_tP = (2 + 0 + 1 + 1 – 2 –2) / 4 = 0, и точка t является внешней.

Алгоритм определения принадлежности точки методом углов состоит в переборе всех сторон многоугольника и вычислении индекса точки.

Предполагая, что структура точки содержит все необходимые операции, разработаем функцию, реализующую тест на принадлежность методом углов.

int Polygon::isin(Point t)

{

int i, ind = 0;

// вначале индекс = 0

Point q = p[n - 1];

// начальная сторона p(n-1)p(0)

for(i = 0; i < n; i++)

{

if(t.code(q) == t.code(p[i]));       // приращение индекса = 0

else if((t.code(p[i]) - t.code(q) + 3)%4 == 0)

ind++;                    // приращение индекса = 1

else if((t.code(p[i]) - t.code(q) + 1)%4 == 0)

ind--;               // приращение индекса = -1

else if((p[i] - q) * (t - q) > 0) ind += 2;

// приращение индекса = 2

else ind -= 2;       // приращение индекса = -2