Метод прогонки для трехдиагональных матриц, страница 4

2) на каждом из отрезков функция является полиномом второй степени вида

, ;

3) функция – интерполяционная функция, то есть:, ;

4) краевому условию .

Отметим, что, отбросив условие три, мы получаем определение параболического сплайна.

Пример. Функция

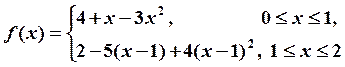
является параболическим сплайном, определенным на отрезке и удовлетворяющим краевому условию . Эта же функция является интерполяционным параболическим сплайном, удовлетворяющим следующей интерполяционной таблице:

	0	1	2
	4	2	1

Теорема существования и единственности. Пусть на отрезке заданы интерполяционная таблица , , причем все узлы сетки различны ( при ) и краевое условие . Тогда существует единственный параболический сплайн такой, что и краевое условие .

Другими словами, если задана интерполяционная таблица , в которой все узлы сетки различны, и краевое условие, то существует единственный интерполяционный параболический сплайн, удовлетворяющий этой таблице и краевому условию.

Нахождение коэффициентов интерполяционного параболического сплайна

Из определения интерполяционного параболического сплайна вытекает система линейных уравнений размерности относительно неизвестных , и , . Эта система линейных уравнений имеет единственное решение, если все узлы сетки различны. Система линейных уравнений легко решается, и мы можем записать следующие явные формулы для нахождения коэффициентов , и :

, , ;

Отметим, что мы привели формулы для случая левого краевого условия . Для правого краевого условия формулы записываются аналогично.

Теорема (оценка погрешности). Пусть . Тогда для любой точки справедлива следующая оценка погрешности: , где , положительная константа не зависит от .

Из оценки погрешности вытекает, что при уменьшении равномерного шага в два раза погрешность интерполяции параболическим сплайном уменьшается в восемь раз.

Производная интерполяционного параболического сплайна – это непрерывная кусочно-линейная функция, то есть линейный сплайн: , , . Отметим, что производная интерполяционного сплайна – это сплайн, который не является интерполяционным.

Нахождение значений интерполяционного параболического сплайна

и его производной

Как и в случае линейного сплайна, сначала находим номер отрезка, содержащего точку , по формуле: .

Зная все коэффициенты , , и номер отрезка, находим значение интерполяционного параболического сплайна в точке , принадлежащей отрезку ,

Как и для линейного сплайна, введем дополнительные коэффициенты: , , . Эти коэффициенты потребуются для вычисления и в точке . Значение производной интерполяционного параболического сплайна в точке , принадлежащей отрезку , вычисляется по формуле

Сложность вычислительного алгоритма построения интерполяционного параболического сплайна. Число арифметических действий, необходимых для построения интерполяционного параболического сплайна, пропорционально числу отрезков (), объем памяти также пропорционален числу отрезков ().

Пример. Приведем текст программы, которая по интерполяционной таблице и левому краевому условию строит интерполяционный параболический сплайн и его производную. Интерполяционная таблица строится на отрезке , с равномерным шагом , где . Узлы сетки вычисляются по формуле , где , , значениянаходятся по формуле Задано краевое условие . На печать выдаются значения интерполяционного параболического сплайна и функции производной интерполяционного параболического сплайна и производной функции в точке .