d Iя/dt= (Uc-2*C*V*Ф-2*Rя*Iя-2*Rв*Iв-2* Lв*d Iв/dt-2*Pв*Wв*dФ/dt)/ 2*Lя
d Iв/dt=( Rш*(Iя -Iв)+ Lш*d Iя/dt-2*Rв*Iв-2*Pв*Wв*dФ/dt)/ 2* Lв+ Lш
dФ/dt=( f(Iвих)-Ф)* Wв/ gвих*kф.
Отсюда:
dФ/dt=( f(Iвих)-Ф)* Wв/ gвих*kф
d Iя/dt=( Uc-2*С*V*Ф-2* Rя*Iя +(2* Lв/(2* Lв+ Lш) -1)*2* Rв*Iв +(2* Lв/(2* Lв+ Lш) -1)*2* Pв* Wв* dФ/dt -2* Lв* Rш/(2* Lв+ Lш)*( Iя –Iв))/(2* Lя+2*Lв*Lш/(2* Lв+ Lш))
d Iв/dt=( Rш*(Iя -Iв)+ Lш*d Iя/dt-2*Rв*Iв-2*Pв*Wв*dФ/dt)/ 2* Lв+ Lш.
Начальные условия.
Характеристики намагничивания ТЭД.
|
Iв, А |
0 |
100 |
200 |
250 |
300 |
350 |
400 |
450 |
500 |
550 |
600 |
650 |
|
Ф, Вб |
0 |
0.0422 |
0.0633 |
0.0785 |
0.0855 |
0.0911 |
0.0954 |
0.0992 |
0.1024 |
0.1052 |
0.1077 |
0.1082 |
Iя=500 А – ток якоря;
Iв=250 А – ток возбуждения;
Ф=0.0785 Вб – магнитный поток ;
V=(Uc-2*( Rя+ Rв)* Iя)/2*C*Ф=66.1 км/ч – скорость ЭПС.
Требуется численно решить задачу Коши для дифференциального уравнения первого порядка с применением функции ode23 системы Matlab на интервале времени.
Простейшее обращение к любой функции ode*** имеет следующий вид:
[tout, yout]=ode***(fun, tspan, yo)
Здесь:
- fun- указатель на функцию вычисления правых частей дифференциального уравнения;
- tspan- вектор, содержащий «контрольные значения» независимой переменной; минимальный вариант tspan=[t0 tfinal] (начальное и конечное значения независимой переменной), но могут быть заданы и промежуточные значения, тогда tspan=[t0 t1 … tfinal];
- yo- начальное значение зависимой переменной (скаляр или вектор-столбец);
- tout- вектор-столбец контрольных значений независимой переменной; если используется минимальный вариант для tspan, выдаются все значения, которые получались в процессе численного интегрирования; если tspan содержит и другие значения кроме t0 и tfinal, то tout= tspan’;
- yout- решение, представленное массивом, в котором каждая строка соответствует одному элементу в столбце tout.
6 .Основная идея методов Рунге-Кутта, формулы 2-го, 4-го порядков, погрешности на шаге, на интервале. Вывод формул 2-го порядка.
Основная идея методов заключается в построении такой вычислительной схемы, которая позволяла бы получать приближенное решение со сколь угодно малой погрешностью и при этом не требовала бы вычисления старших производных.
Пусть приближенное решение yk+1=yk+h*Ф (xk, yk, h).Функция Ф – уточняющая. Построим эту функцию так, чтобы погрешность приближенного решения была величиной сколь угодно малой по сравнению с шагом h и не содержала производных от правой части дифференциального уравнения y'=f (x, y). Построим вычислительную схему порядка о(h^3 ) на шаге, и о(h^2 ) на интервале.
Пусть Ф(x, y, h)=c1*f (x, y)+c2*f (x+a*h, y+b*h*f (x, y)),
где c1, c2, a, b – постоянные.
Ф – функция двух переменных, поэтому её можно разложить по формуле Тейлора.
Ф(xk, yk, h)=c1*f (xk, yk)+c2*f (xk, yk)+c2*(df(xk, yk)/dx)*h*a+ +c2*(df(xk, yk)/dy)*b*h*f (xk, yk)+o(h ).
Тогда yk+1=yk+c1*h*f (xk, yk)+c2*h*f (xk, yk)+c2*(df(xk, yk)/dx)*h*a+c2*(df(xk, yk)/dy)*b*h*f (xk, yk)+o(h ).*
В то же время вычислительную схему заданного порядка можно записать по формуле Тейлора для функции одной переменной.
Yk+1=yk+h*f (xk, yk)+h /2! * y’’(xk, yk)+o(h )**
Значения входящих в это выражение производных можно получить последовательным дифференцированием основного уравнения задачи.
y’=f (x, y)
y’’=df(xk, yk)/dx+df (xk, yk)/dy * f (xk, yk).
Сравнивая выражения (*) и (**), получаем систему:
c1+c2=1
Принято считать c2=c1=1/2 ; a=b=1.
Получаем формулу Рунге-Кутта 2-го порядка:
yk+1=yk+h/2 *(k1+k2), где
k1=f (xk, yk);
k2=f (xk+h, yk+h*k1).
Наиболее распространенной в инженерной практике является вычислительная схема метода Рунге-Кутта 4-го порядка.
yk+1=yk+h/6 *(k1+2*k2+2*k3+k4), где
k1=f (xk, yk);
k2=f (xk+h/2, yk+h/2 *k1);
k3=f (xk+h/2, yk+h/2 *k2);
k4=f (xk+h, yk+h*k3);
k=0, 1…(N-1).
Погрешность на шаге о(h^5).
Погрешность на интервале о(h^4).
1. Описание конструкции, системы и явления. Применение в работе электроподвижного состава.
2. Формулировка инженерной задачи.
3. Эквивалентная расчетная схема, описание, задание параметров.
4. Система дифференциальных уравнений, составленных по законам для электрических цепей (Кирхгофа, Ленца), по построенной схеме.
5. Формулировка математической задачи. Приведение системы дифференциальных уравнений к каноническому виду. Начальные условия.
6. Основная идея методов Рунге-Кутта, формулы 2-го, 4-го порядков, погрешности на шаге, на интервале. Вывод формул 2-го порядка.
7. Краткое описание возможностей среды программирования PC MATLAB для решения практических инженерных задач.
8. Решение вычислительной задачи. Описание вариантов изменения параметров схемы и результаты вычислений.
9. Анализ и практические выводы по результатам численного решения.
10. Список литературы.
8. Решение вычислительной задачи.
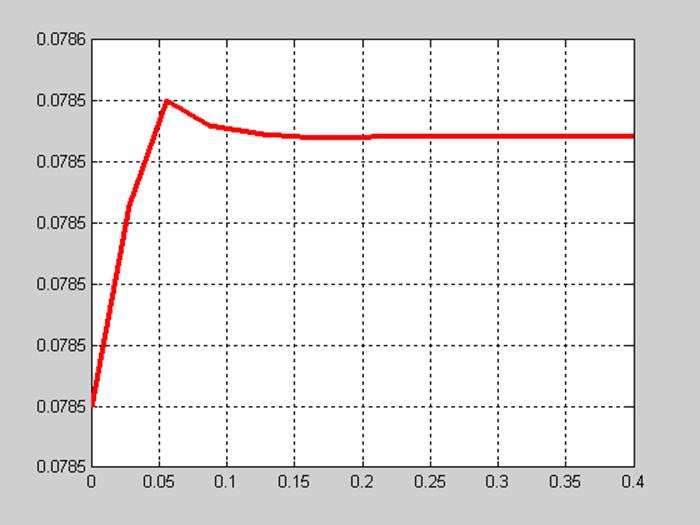
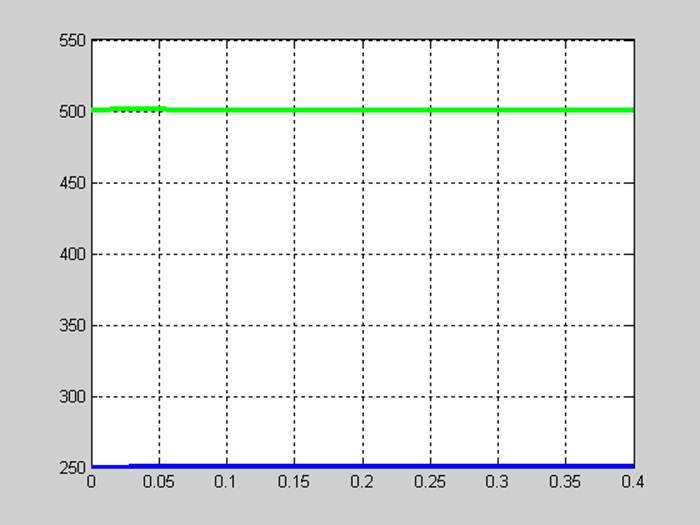
При Ф=0.0785 Вб , Iя=500 А, Iв=250 А .
% Отрыв токоприемника при ОВ
global U Ra Rb Rsh Lsh KF Lb La IT FF R1 R2 R3 R4
U=3000; Ra=0.035; Rb=0.03; Wb=19; Rsh=0.06; Lsh=0.0045;
gvx=14127; c=284.1; V=66.1; Lb=0.0038; La=0.003; Pb=3;
R1=Wb/gvx; R2=2*c*V; R3=2*Lb/(2*Lb+Lsh); R4=2*Pb*Wb;
IT=[0 100 200 250 300 350 400 450 500 550 600 650];
FF=[0 0.0422 0.0633 0.0785 0.0855 0.0911 0.0954 0.0992 0.1024 0.1052 0.1077 0.1082];
AP=polyfit(IT,FF,5);
KF=[5*AP(1) 4*AP(2) 3*AP(3) 2*AP(4) AP(5)];
[T,Y]=ode23(@praw, [0,0.4],[0.0785 500 250]);
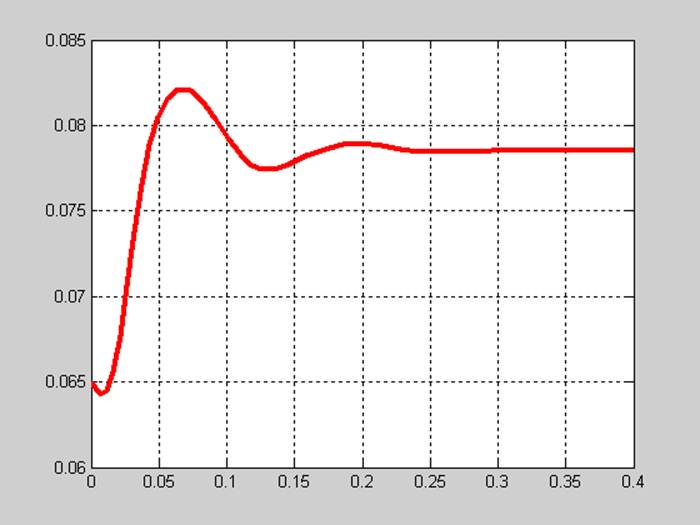
figure(1);plot(T,Y(:,1),'r','LineWidth',3);grid;
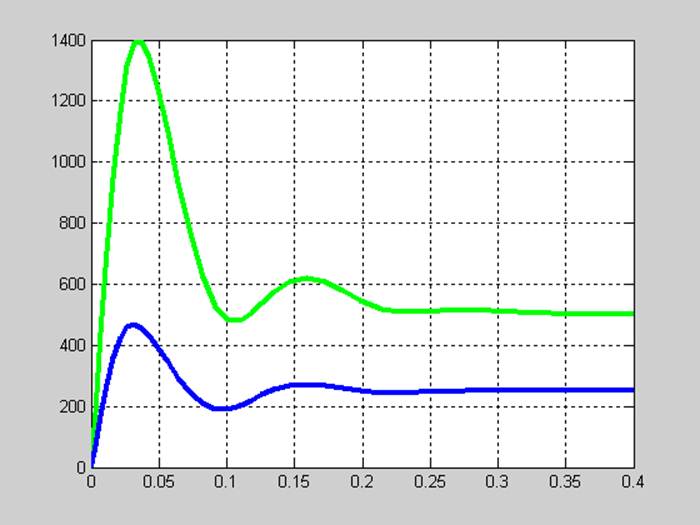
figure(2);plot(T,Y(:,2),'g',T,Y(:,3),'b','LineWidth',3);grid;
function F=praw(t,y)
global U Ra Rb Rsh Lsh KF Lb La IT FF R1 R2 R3 R4
F=zeros(3,1);
F(1)=(spline(IT,FF,y(3))-y(1))*R1/polyval(KF,y(3));
F(2)=(U-R2*y(1)-2*Ra*y(2)+2*Rb*(R3-1)*y(3)+R4*(R3-1)*F(1)-Rsh*R3*(y(2)-y(3)))/(2*La+Lsh*R3);
F(3)=(Rsh*(y(2)-y(3))+Lsh*F(2)-2*Rb*y(3)-R4*F(1))/(2*Lb+Lsh);
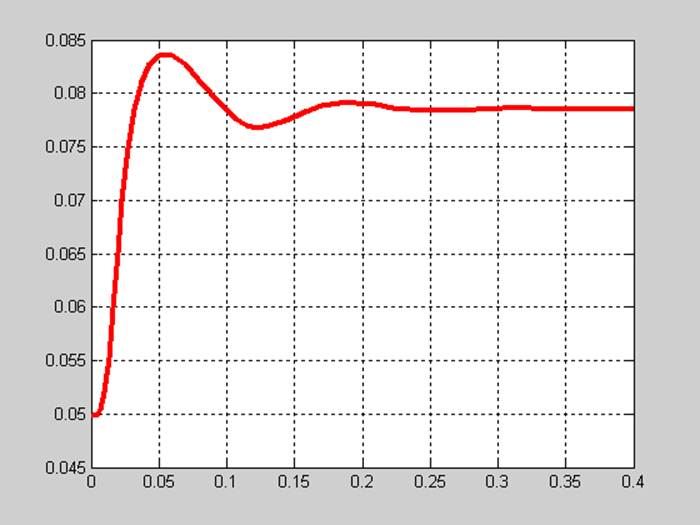
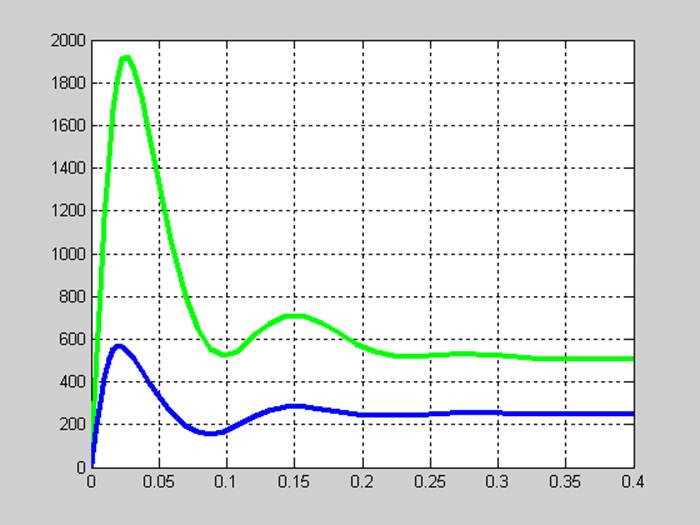
При Ф=0.05 Вб , Iя=0 А, Iв=0 А .
% Отрыв токоприемника при ОВ
global U Ra Rb Rsh Lsh KF Lb La IT FF R1 R2 R3 R4
U=3000; Ra=0.035; Rb=0.03; Wb=19; Rsh=0.06; Lsh=0.0045;
gvx=14127; c=284.1; V=66.1; Lb=0.0038; La=0.003; Pb=3;
R1=Wb/gvx; R2=2*c*V; R3=2*Lb/(2*Lb+Lsh); R4=2*Pb*Wb;
IT=[0 100 200 250 300 350 400 450 500 550 600 650];
FF=[0 0.0422 0.0633 0.0785 0.0855 0.0911 0.0954 0.0992 0.1024 0.1052 0.1077 0.1082];
AP=polyfit(IT,FF,5);
KF=[5*AP(1) 4*AP(2) 3*AP(3) 2*AP(4) AP(5)];
[T,Y]=ode23(@praw, [0,0.4],[0.05 0 0]);
figure(1);plot(T,Y(:,1),'r','LineWidth',3);grid;
figure(2);plot(T,Y(:,2),'g',T,Y(:,3),'b','LineWidth',3);grid;
При Ф=0.065 Вб , Iя=0 А, Iв=0 А .
% Отрыв токоприемника при ОВ
global U Ra Rb Rsh Lsh KF Lb La IT FF R1 R2 R3 R4
U=3000; Ra=0.035; Rb=0.03; Wb=19; Rsh=0.06; Lsh=0.0045;
gvx=14127; c=284.1; V=66.1; Lb=0.0038; La=0.003; Pb=3;
R1=Wb/gvx; R2=2*c*V; R3=2*Lb/(2*Lb+Lsh); R4=2*Pb*Wb;
IT=[0 100 200 250 300 350 400 450 500 550 600 650];
FF=[0 0.0422 0.0633 0.0785 0.0855 0.0911 0.0954 0.0992 0.1024 0.1052 0.1077 0.1082];
AP=polyfit(IT,FF,5);
KF=[5*AP(1) 4*AP(2) 3*AP(3) 2*AP(4) AP(5)];
[T,Y]=ode23(@praw, [0,0.4],[0.065 0 0]);
figure(1);plot(T,Y(:,1),'r','LineWidth',3);grid;
figure(2);plot(T,Y(:,2),'g',T,Y(:,3),'b','LineWidth',3);grid;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.