3. Метод «классики»
Данная схема состоит из двух проходов.
При первом проходе величина ![]() вычисляется в тех узлах сетки, в которых (i+j+n)
является четным числом по простой явной схеме
вычисляется в тех узлах сетки, в которых (i+j+n)
является четным числом по простой явной схеме
Проход 1.
Если (i+j+n) - четное число, то
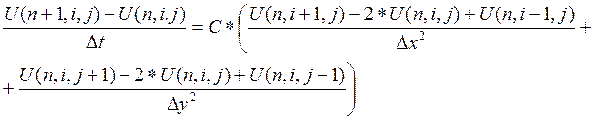
При втором проходе ![]() вычисляется в тех узлах сетки, в которых (i+j+n)
является нечетным числом по простой неявной схеме.
вычисляется в тех узлах сетки, в которых (i+j+n)
является нечетным числом по простой неявной схеме.
Проход 2.
Если (i+j+n) - нечетное число, то
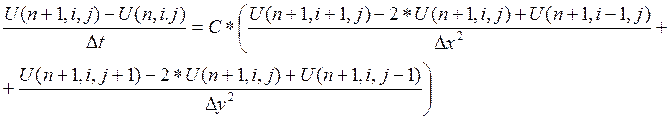
Второй проход только кажется неявным. Однако, получающаяся при
переходе от одного временного слоя к другому система линейных алгебраических
уравнений такова, что в каждом из них содержится только по одному неизвестному,
т.к. величины ![]() уже
известны из первого прохода, т.е. рассматриваемая схема является явной.
уже
известны из первого прохода, т.е. рассматриваемая схема является явной.
Схема двухслойная по времени. Имеет первый порядок аппроксимации. Точнее - первый порядок точности по времени и второй - по пространству. Таким образом, нестационарное решение имеет первый порядок аппроксимации, а стационарное (независящее от времени, установившееся) - второй. Так как нас интересует эллиптическое уравнение (3), то получаемое для него установившееся решение имеет второй порядок точности.
Схема абсолютно согласована.
Схема абсолютно устойчива.
Обладает только диссипативными ошибками. Дисперсионные ошибки отсутствуют.
Шаги по времени можно рассматривать как отдельные итерации для нахождения решения поставленной задачи. Условия прекращения процесса установления те же, что и в предыдущем случае п.2.
4. Неявный метод переменных направлений.
Шаг 1
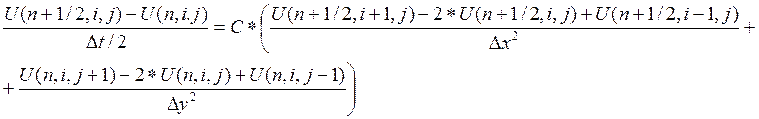
Шаг 2
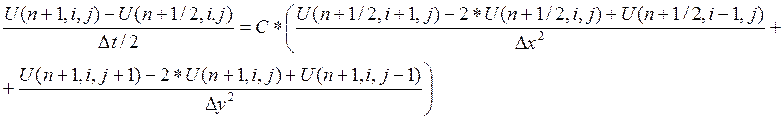
Метод предусматривает «расщепление» задачи по направлениям – «x», «y».
На первом шаге неявно выписывается только вторая производная по «x». Вторая производная по «y» при этом представляется явным способом.
На втором шаге они меняются местами - неявно выписывается только вторая производная по «y». Вторая же производная по «x» представляется явным способом.
Задача на каждом шаге сводится к решению систем линейных алгебраических уравнений с трехдиагональной матрицей. Это дает значительную экономию количества требующихся действий для получения ее решения. На шаге 1 такая система решается для каждой строки (ряда точек с фиксированным индексом j), а на шаге 2 – для каждого столбца (ряда точек с фиксированным индексом i).
Коэффициент перехода этой схемы равен 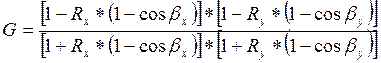 , причем мнимая часть этого
коэффициента равна нулю
, причем мнимая часть этого
коэффициента равна нулю ![]() . Следовательно, сдвиг по фазе (фазовые
ошибки) отсутствуют. Имеются только амплитудные (диссипативные) ошибки,
определяемые модулем
. Следовательно, сдвиг по фазе (фазовые
ошибки) отсутствуют. Имеются только амплитудные (диссипативные) ошибки,
определяемые модулем ![]() .
.
Схема двухшаговая, неявная, двухслойная по времени. Точнее, трехслойная – с «промежуточным» полуслоем (t+∆t/2), [т.е. (n+1/2)] по времени.
Имеет второй порядок аппроксимации. Установившееся решение также имеет второй порядок точности.
Схема абсолютно согласована.
Схема абсолютно устойчивости.
Обладает только диссипативными ошибками. Дисперсионные ошибки отсутствуют.
Шаги по времени можно рассматривать как отдельные итерации для нахождения решения поставленной задачи. Условия прекращения процесса установления те же, что и в предыдущем случае п. 2.
5. Метод Яненко Н.Н. (метод дробных шагов или метод расщепления)
Основная идея метода дробных шагов состоит в расщеплении конечно-разностного оператора на ряд одномерных операторов. Например, к простой неявной схеме решения двумерного уравнения теплопроводности можно применить метод расщепления следующим образом:
Шаг 1
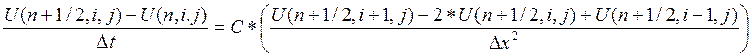
Шаг 2
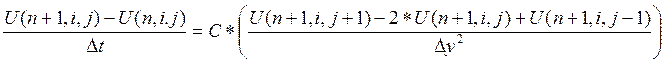
Здесь применено расщепление по пространству по координатам «x» , «y» рассматриваемого двумерного пространства
На первом шаге неявно выписывается только вторая производная по «x».
На втором шаге неявно выписывается только вторая производная по «y».
Задача на каждом шаге сводится к решению систем линейных алгебраических уравнений с трехдиагональной матрицей. Это дает значительную экономию количества требующихся действий для получения ее решения.
Схема двухшаговая, неявная, двухслойная по времени. Точнее, трехслойная – с «промежуточным» полуслоем (t+∆t/2), [т.е. (n+1/2)] по времени.
Имеет первый порядок аппроксимации. Точнее - первый порядок точности по времени и второй - по пространству. Таким образом, нестационарное решение имеет первый порядок аппроксимации, а стационарное (независящее от времени, установившееся) - второй. Так как нас интересует эллиптическое уравнение (3), то получаемое для него установившееся решение имеет второй порядок точности.
Схема абсолютно согласована.
Схема абсолютно устойчива.
Обладает только диссипативными ошибками. Дисперсионные ошибки отсутствуют.
Шаги по времени можно рассматривать как отдельные итерации для нахождения решения поставленной задачи. Условия прекращения процесса установления те же, что и в предыдущем случае п.2.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.