вынужденных колебаний механической системы с одной степенью свободы. Математическая модель служит для исследования колебательной системы и определения различных режимов колебаний.
Если t≤ t![]() , то действия повторяется, начиная с пункта 6; если t
>t
, то действия повторяется, начиная с пункта 6; если t
>t![]() , то вычисления завершаются.
, то вычисления завершаются.
Например, требуется определить динамическую реакцию двух массовой не демпфированной колебательной модели рис. 1а,б подверженный воздействию постоянной силы. Колебательный процесс такой модели описывается системой дифференциальных уравнений второго порядка:
![]() m
m![]() u
u![]() + k
+ k![]() (u
(u![]() -u
-u![]() )=0;
)=0;
m![]() u
u![]() - k
- k![]() (u
(u![]() -u
-u![]() )+k
)+k![]() u
u![]() =q; где u
=q; где u![]() │
│![]() = u
= u![]() │
│![]() =0; u
=0; u![]() │
│![]() = u
= u![]() │
│![]() =0;
=0;
или в матричной форме
Mu+Ku=p,
Где
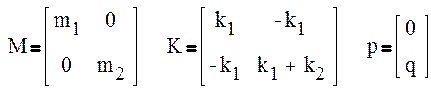 |
m![]() =10; m
=10; m![]() =10; k
=10; k![]() =10; k
=10; k![]() =10; q=10.
=10; q=10.
Изложенная выше последовательность действий по θ –
методу Вильсона при наблюдении за данной моделью с момента времени t![]() =0 до t
=0 до t![]() =25 (шаг
дискретизации h=1 c.) содержится в БЕЙСИК-программе. Смысл принятых
обозначения в алгоритме и программе представлен в приложениях.
=25 (шаг
дискретизации h=1 c.) содержится в БЕЙСИК-программе. Смысл принятых
обозначения в алгоритме и программе представлен в приложениях.
1. С помощью математического моделирования получаем эталонные графики колебательных процессов для математической модели материальной точки при определённых (оптимальных) значениях коэффициентов жесткости пружины и различных значениях масс, соответствующих определённой статической нагрузке.
2. Расчётным путём определяются все необходимые параметры. 3. Строятся сводные графики полученных расчетов.
4. Производим аппроксимацию функций.
а) б)
![]()
![]()

![]()
|
E![]() F
F![]()
![]()
 a
a![]()
P![]()
k![]()
 |
|||||
|
|||||
y![]()
E![]() F
F![]() a
a![]()
 |
|||
P![]()
k![]()
Рис. 1 Двух массовая не демпфированная колебательная модель (а) и её конечно-элементный аналог (б).
2.2. Исходные данные и результаты
Задача № 1
НаименованиеПеременных |
Описание переменных |
|
R1,R2,R3 ( ) |
Длины звеньев |
P ( ) |
|
|
ά |
|
|
T |
|
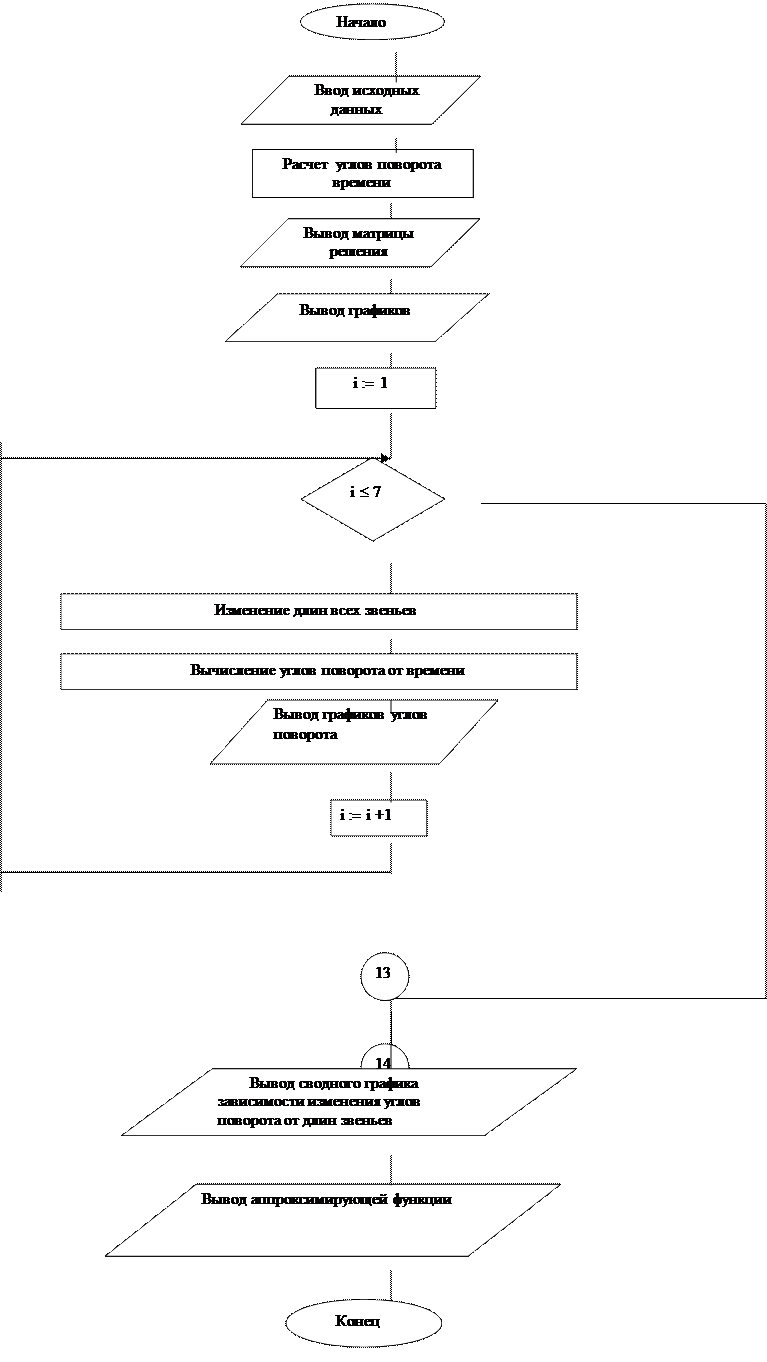
2.3. Общая графическая схема решения задачи и ее описание.
 |
||
 |
||
Рис. 2 Графическая схема
Описание графической схемы решения
1. Присваиваем известным величинам их значения.
2. Решаем систему дифференциальных уравнений с помощью функции rkfixed.
3. Выводим матрицу решений.
4. Выводим графики изменения углов поворота от времени.
5. Начало проведения опытов ( i – номер опыта )
6. Количество опытов равняется 7
7. В каждом опыте длину звеньев математической модели.
8. Вычисляем углы поворота в зависимости от изменений длин звеньев.
9. Вывод графиков углов поворота как результата.
11. Изменяем номер опыта.
12. Выводим сводные графики зависимостей изменения углов поворота от изменений длин звеньев.мат.модели .
13. Выводим аппроксимирующую зависимость.
14. Конец. [Рис. 2 ]
2.4. Планирование исследований.
При решении задачи необходимо провести ряд опытов в которых исследуется влияние изменения длин звеньев математической модели на графики углов поворота механизма.
|
Изменяемые параметры |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
R1 |
0.93 |
1.93 |
2.93 |
3.93 |
4.93 |
5.93 |
6.93 |
|
Изменяемые параметры |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
R2 |
0.67 |
1.67 |
2.67 |
3.67 |
4.67 |
5.67 |
6.67 |
|
Изменяемые параметры |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
R3 |
0.87 |
1.87 |
2.87 |
3.87 |
4.87 |
5.87 |
6.87 |
3. Описание документа исследования.
По результатам опытов строится аппроксимирующая функция. Для чего задаются вектора Cr и Ac приложение стр. .
После чего находятся максимальные амплитуды перемещения , для чего строится вектор S.
Проводим аппроксимацию по методу наименьших квадратов при помощи функции pspline приложение стр. . Задаются дискретные переменные i :=0..10 и v := 0..10
Точечная зависимость максимальных амплитуд от длины строится в i точках, а аппроксимация в v точках.
Все эти функции вычисляют вектор коэффициент вторых производных исходной функции заданной таблично.
Для получения инерполяции функции применяется стандартная функция вида: TP (r) := interp (K,Cr,Ac,v)
Где – Cr ,Ac –те же значения
К – вектор коэффициент вторых производных сплайн интерполяции
Строится аппроксимирующая функция на одном поле с зависимостью
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.