











Міністерство освіти і науки України
Донбаський державний технічний університет
Кафедра електронних систем
Сафронов П.С.
ОПОРНИЙ КОНСПЕКТ ЛЕКЦІЙ
з дисципліни
"Аналіз електронних схем"
для спеціальності 6.090803 "Електронні системи"
Алчевськ 2006
Відшукання робочої точки або розрахунок за постійним струмом електричних ланцюгів зазвичай є першим кроком при аналізі нелінійних схем. Він включає визначення вузлової напруги в схемі при даних параметрах джерел постійного струму і вимагає рішення систем нелінійних рівнянь.
Це може бути виконано за допомогою алгоритму Ньютона – Рафсона для декількох змінних.
Моделі активних приладів зазвичай включають експоненціальні функції, які можуть утрудняти обчислення. Отримавши рішення по постійному струму, проектувальник може зацікавитися його чутливістю по відношенню до параметрів ланцюга. У багатьох випадках нелінійні функції, що містяться в моделях діодів і транзисторів, відомі у вигляді таблиць, а не формул. У цій ситуації можлива шматкова лінеаризація між заданими точками.
Алгоритм Ньютона – Рафсона (Н – Р) був введений раніше як один з методів відшукання коріння поліномів. Він добре відомий, широко використовується і має квадратичну збіжність, якщо початкове наближення близьке до точного рішення. Розглянемо його застосування для вирішення рівнянь ланцюгів.
При рішенні
рівняння ![]() в скалярному випадку ітерації Н – Р
визначаються виразом
в скалярному випадку ітерації Н – Р
визначаються виразом
![]() (1.1)
(1.1)
Для окремих ланцюгів можливе виключення деяких змінних і зведення завдання до одного рівняння.
Для схем з двома і більш нелінійних елементів застосовують метод рішення систем нелінійних рівнянь.
Розглянемо
систему n нелінійних рівнянь для ![]() з
n змінними
з
n змінними ![]() :
:
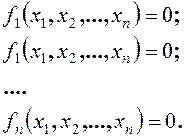 (1.2)
(1.2)
Позначимо вектор змінних через х і вектор функцій через f. Тоді (1.2) вдається записати у формі
f(х)=0. (1.3)
Припустимо, що система рівнянь має рішення; позначимо його через х*. Припустивши, що х близько до х*, нехтуватимемо членами високого порядку і запишемо систему рівнянь в лінеаризованій формі
![]() (1.4)
(1.4)
де М – матриця Якобі функції f.
Якщо прирівняти нулю систему рівнянь (1.4), то рішення не буде рівне вектору х* (оскільки нехтували членами високого порядку). В результаті набудемо деякого нового значення х. Використовуючи верхні індекси для позначення послідовності ітерацій, отримуємо
![]() . (1.5)
. (1.5)
Формальне рішення (5) визначається як
![]() (1.6)
(1.6)
На практиці ж матриця Якобі не звертається. Позначивши
![]() (1.7)
(1.7)
отримаємо
![]() . (1.9)
. (1.9)
Рішення знайдемо
за допомогою LU-факторизації, значення ![]() визначаємо
з виразу
визначаємо
з виразу
![]() (1.10)
(1.10)
Вирази (1.9) і (1.10) представляють алгоритм Н – Р для систем рівнянь. Його ще називають як рівняння Ньютона – Рафсона. Алгоритм має швидку збіжність (квадратичну поблизу точки рішення). Його недолік полягає в необхідності розрахунку матриці Якобі.
При відшуканні рішення по постійному струму в деякому ланцюзі всі котушки індуктивності в ній закорачиваються, а всі конденсатори виключаються.
Формальний опис алгоритму:
1. Рівняння для вузлових потенціалів вимагають, щоб резистори з нелінійним опором описувалися рівнянням у формі
![]() (1.11)
(1.11)
Індекс b позначатиме напругу на гілки і струм в ній. Для вузлів використовуватимемо індекс n. Додатково слідує всі джерела в ланцюзі замінити джерелами струму.
2. Отримують Якобіан як диференціал складної функції
3. Визначають напругу на гілках.
3. Знаходять струми гілок.
4. Розраховують матрицю провідності. Для резисторів з лінійними опорами елементи матриці співпадають із значеннями їх провідності.
5. Визначають Якобіан.
6. Знайти значення векторної функції в точці.
7. Вирішують систему рівнянь.
8. Набути значень вузлових потенціалів.
9. Якщо збіжність не досягнута, переходять до кроку 3.
При відшуканні режиму по постійному струму в схемах з діодами і біполярними транзисторами метод Н – Р може сходитися, але на деяких ітераційних кроках виникають труднощі в обчисленнях на ЕОМ. Вони викликані переповнюванням розрядної сітки машини.
Припустимо, що на
к-йітерації отримана точка ![]() і алгоритм
передбачив на лінеаризованій характеристиці нову точку
і алгоритм
передбачив на лінеаризованій характеристиці нову точку ![]() з
відповідним новим значенням
з
відповідним новим значенням ![]() . У стандартній
процедурі потрібно розрахувати значення функції
. У стандартній
процедурі потрібно розрахувати значення функції ![]()
![]() . Оскільки експоненціальна функція
росте надзвичайно швидко для позитивних значень, це може спричинити за собою
переповнювання сітки ЕОМ.
. Оскільки експоненціальна функція
росте надзвичайно швидко для позитивних значень, це може спричинити за собою
переповнювання сітки ЕОМ.
Один з можливих засобів в цій ситуації полягає у використанні крапки, що отримується на кривій при русі по горизонталі замість переміщення по вертикалі. Інверсія діодної характеристики дає нову напругу. Горизонтальну проекцію можна використовувати для всієї напруги, що перевищує 0,7 В, а вертикальну – для напруги, меншої вказаного порогу
Інше евристичне
правило рекомендує використовувати горизонтальну проекцію, коли![]() , а вертикальну – у протилежному
випадку.
, а вертикальну – у протилежному
випадку.
Часовий відгук електронної схеми можна знайти чисельною інтеграцією диференціальних рівнянь, що описують процеси в цій схемі. Методи чисельної інтеграції діляться на дві великі групи. У першій групі використовуються співвідношення, що спираються на лінійні багатокрокові (ЛБ) формули, в другій – на формули Рунге—Кутта (Р–К). Розглянемо ЛБ формули: пряма і зворотна формули Ейлера і формула трапецій. Методи, в яких використовуються формули Р–К, застосовуються давно. Проте, на відміну від методів першої групи, вони не знайшли такого широкого розповсюдження при розрахунку електронних схем на ЕОМ.
Диференціальне рівняння, яке повинне проінтегрувати, має вигляд
![]() (2.1)
(2.1)
де t – час.
Відповідний цьому рівнянню інтеграл
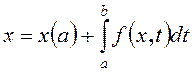 (2.2)
(2.2)
Припустимо, що відоме
наближене рішення ![]() в точці
в точці ![]() . Потрібно отримати рішення
. Потрібно отримати рішення ![]() в момент
в момент![]() ,
ввівши крок за часом
,
ввівши крок за часом
![]() . (2.3)
. (2.3)
Якщо вирішувати
починають при t0, то початкове значення ![]() відоме. Для будь-яких інших
відоме. Для будь-яких інших ![]() чисельне значення
чисельне значення ![]() буде в загальному випадку відмінно
від точного рішення
буде в загальному випадку відмінно
від точного рішення ![]() . Оскільки
. Оскільки ![]() відомо, можемо розрахувати
відомо, можемо розрахувати ![]() по формулі (2.1) і набути
наближеного значення, прийнявши, що при зміні t від t0 до
t1 функція
по формулі (2.1) і набути
наближеного значення, прийнявши, що при зміні t від t0 до
t1 функція ![]() залишається
постійною і рівною
залишається
постійною і рівною ![]() .
.
Тоді
![]() (2.4)
(2.4)
Цей вираз відомий
як пряма формула Ейлера, шукана функція була апроксимована на кроці інтеграції
прямої, співпадаючої з дотичною до цієї функції в точці ![]() .
Помилка розрахунку тим більше, чим більше розмір кроку
.
Помилка розрахунку тим більше, чим більше розмір кроку ![]() .
.
Можна виразити ![]() через значення
через значення ![]() і похідну
і похідну ![]() .Для
цього потрібно, як і раніше, прийняти, що функція
.Для
цього потрібно, як і раніше, прийняти, що функція ![]() залишається
на інтервалі
залишається
на інтервалі ![]() постійною і рівною
постійною і рівною ![]() . Тоді витікає, що
. Тоді витікає, що
![]() (2.5)
(2.5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.