1. Постановка задачи оптимизации. Основные этапы построения математической модели объекта оптимизации
Оптимизация - Это выбор наилучшего решения. Для этого создаётся математическая модель.
Этапы построения математической модели:
-Определение границ объекта оптимизации – выделение определяющих свойств процесса ,
-выбор управляемых переменных – величин, на которые влияем,
-определение ограничений на управляемые переменные,
-выбор числового критерия оптимизации - выбор целевой функции, отвечающей заданным критериям.
-формулировка математической задачи оптимизации,
- информационное обеспечение математической модели – информация о величинах, параметрах, входящих в модель.
. 2. Задача геометрического программирования. Понятие позинома. Основные свойства позиномов.
Геометрическое программирование есть метод решения одного специального класса задач нелинейного программирования, в которых критерий оптимальности и ограничения задаются в виде позиномов - выражений, представляющих собой сумму произведений степенных функций от независимых переменных. Позином – функция положительная. До некоторого этапа задачу оптимизации решают аналитически, откуда уже отыскивают оптимальное решение. Как правило, этот метод используют для конечных уравнений.
3.Минимум функции многих переменных. Понятие локального и глобального минимума функции.
Пример для функции одной переменной.
 для некоторых функций есть точки локального и
глобального миниума.
для некоторых функций есть точки локального и
глобального миниума.
Глобальный миниум – точка , в которой f(x*)<f(x)
Локальный миниум – точка, в которой f(x*)<f(x) на определённом участке ф-ии.
4.Двойственная функция и двойственная задача. Поиск минимума позинома с помощью двойственной функции
ДВОЙСТВЕННАЯ ЗАДАЧА - инструмент, позволяющий установить, оптимально ли данное допустимое решение задачи линейного программирования, без непосредственного сравнения его со всеми остальными допустимыми решениями. Принято считать прямой задачу, ориентированную на максимум целевой функции, а двойственной — ориентированную на минимум.
5.Дифференцируемые функции многих переменных. Первый и второй дифференциал функции. Понятие градиента функции.
Пусть
функция дифференцируема в точке х0 Є Еn, то её приращение ∆f(x0)=f(x0+∆x) – f(x0) можно записать в виде ∆f(x0)=df(x0)+0(⃒⃒∆x⃒⃒), где df(x0)=![]() – первый дифференциал f(x) в точке х0.
– первый дифференциал f(x) в точке х0.

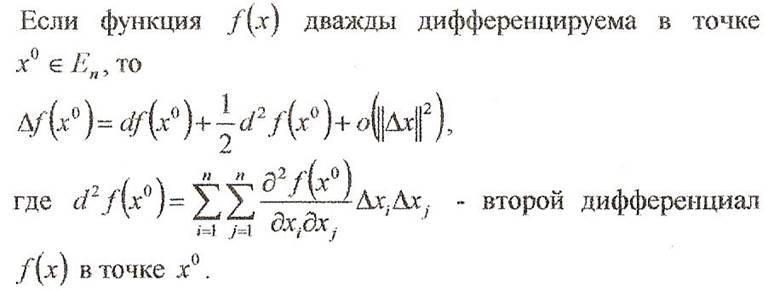
6.Теорема двойственности. Нахождение минимумов позиномов с помощью решения двойственной задачи.


6. Прямые методы безусловной минимизации. Метод правильного симплекса. Алгоритм метода
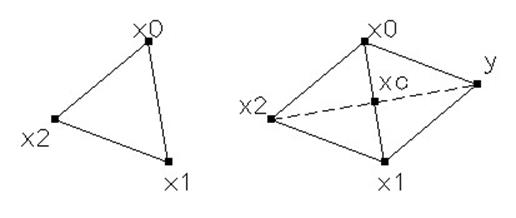
Правильным симплексом называется множество из п +1 точек - вершин симплекса. Отрезок, соединяющий две вершины, - ребро симплекса.
Правильным симплексом является совокупность вершин равностороннего треугольника.
Если x0 - одна из вершин правильного симплекса в En, то координаты остальных п вершин x1,... ,xn можно найти по формуле
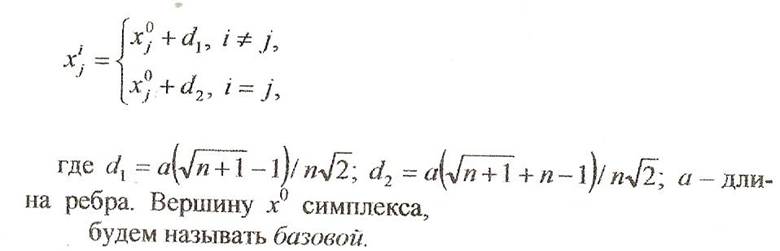
Отражаем вершину х2 , получаем отраженную вершину у


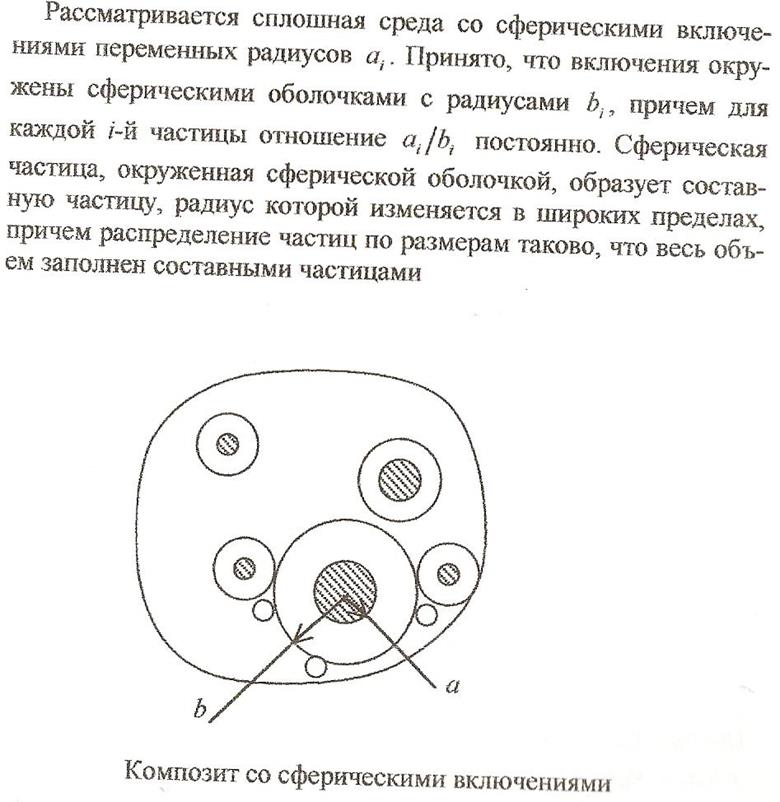
8.Принципы построения моделей композиционных материалов. Представительный элемент объема КМ

9.Методы безусловной минимизации, использующие производные функции. Метод градиентного спуска. Алгоритм метода.

10. Модель полидисперсной среды. Основные допущения при построении этой модели.
Полидисперсная среда:

11. Методы безусловной минимизации, использующие производные функции. Метод наискорейшего спуска. Алгоритм метода.
Метод наискорейшего спуска.

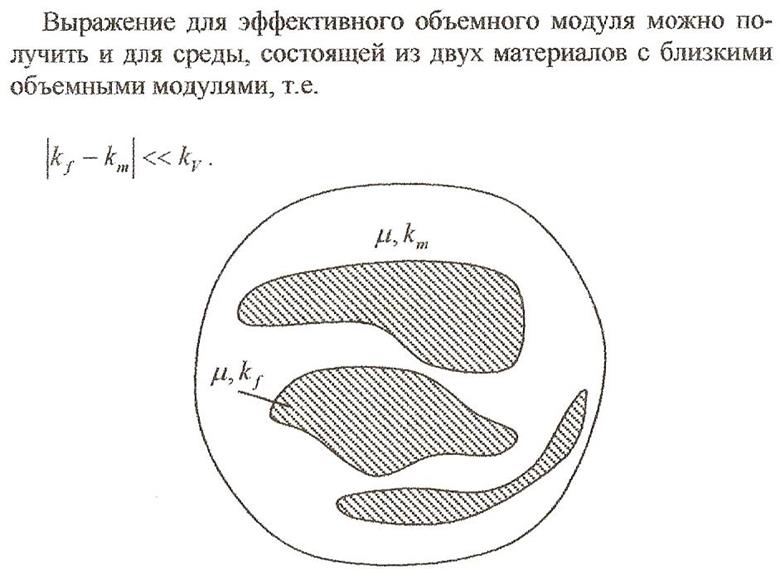
12. Модель композита с равными модулями сдвига фаз. Основные допущения при построении этой модели.

13. Методы безусловной минимизации, использующие производные функции. Метод сопряженных градиентов. Алгоритм метода.

15. Классический метод оптимизации для поиска минимума функции многих переменных. Алгоритм метода.
1.Решим систему уравнений f'(x0)=0и найдем все стационарные точки функции f(x)
2. Используем достаточные условия минимума среди стационарных точек функции f(x) найти точки локального минимума и, сравнивая значения функции в них, найти точку глобального минимума. По критерию Сильвестра - Гессман положительно определенная точка (х) являются точка локального минимума она же точка глобального минимума.
Алгоритм
1.Составляется система уравнений
2. Получаем матрицу А'
16. Полидисперсная модель композита с цилиндрическими включениями. Равнопредставленные композиты
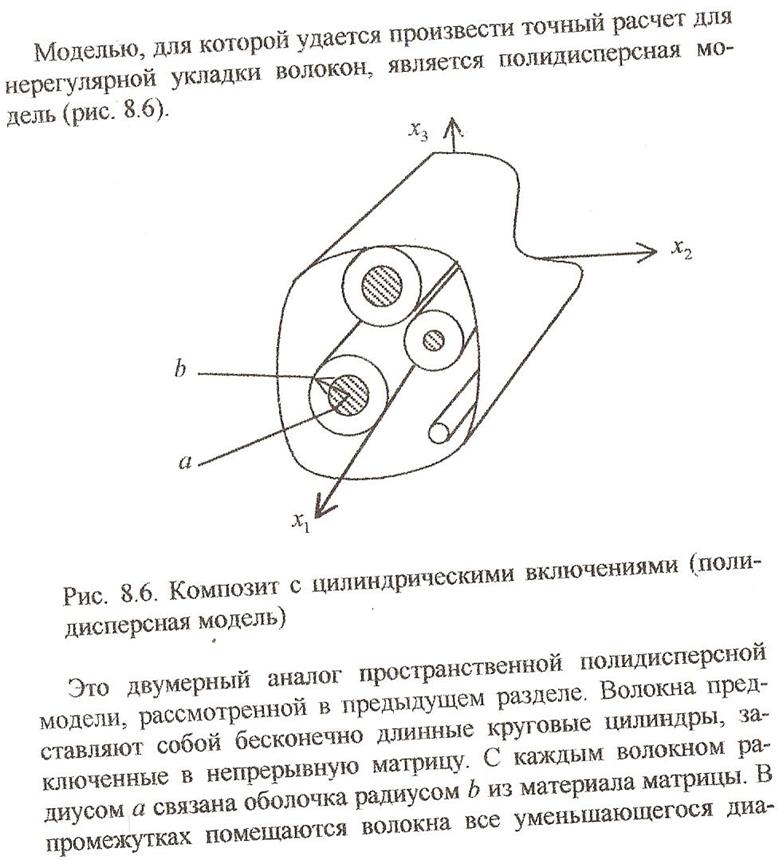

Равнопредставленные композиты
Области занятые наполнителем и матрицей равны, такой композит называется равнопредставленным. Возможен при треугольном сечении волокон.
Модуль
сдвига равнопредставленного материала G23=![]()
17. Методы безусловной минимизации, использующие производные функции. Метод Ньютона. Алгоритм метода.
Метод Ньютона построение последовательности точек таких, что f(xk+1)<f(xk) точки этой последовательности вычисляют по правилу xk+1=xk+pk где начальная точка задаётся пользователем, а направление спуска рк определяется для каждого значения к по формуле: pk=-A-1(xkf'(xk))
Выбор направления поиска гарантирует выполнение требования убывания функции при условии А(хк)>0
Аппроксимация
–описание нескольких точек в виде функции.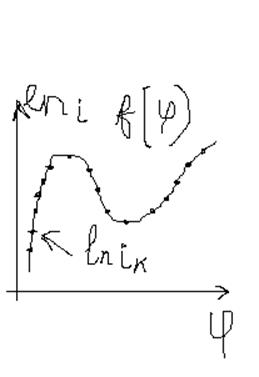
Направление поиска рк определяют из необходимого условия экстремума
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.