Расчет тонкостенных конструкций оболочечного типа. Часть 1: Методические указания (Основы теории тонкостенных оболочек вращения. Расчет оболочек вращения по безмоментной теории), страница 5

Выполним расчет сосуда, состоящего из участков сферической, цилиндрической и конической оболочек (рис.10), по безмоментной теории.

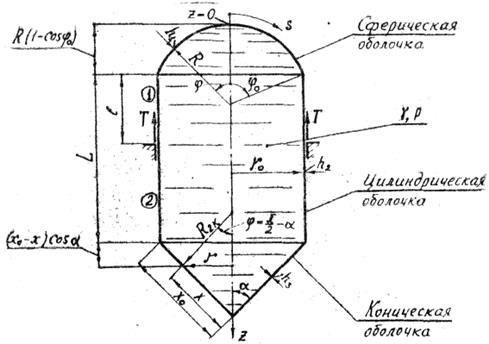
Рис.10. Расчетная схема сосуда

Геометрические размеры сосуда  известны. Заданы также модуль упругости Е и коэффициент Пуассона  m  материала сосуда. Сосуд заполнен жидкостью с плотностью r.  Жидкость находится под давлением p.

Если пренебречь весом сосуда, то реакция кольцевой опоры будет численно равна весу жидкости, заключенной в сосуде:

                                    (9)

где  g =  rg – удельный вес жидкости,   V - объём сосуда.

Расчет сосуда производим по отдельным его элементам.

6.1. Сферическая оболочка

Сферическая оболочка нагружена давлением

                                        (10)

переменным вдоль дуги меридиана.

Главные радиусы кривизны сферической оболочки:

R₁ = R₂=R                                                                    (11)

радиус параллельного круга

r = R sin j                                                                   (12)

Нормальным коническим сечением с углом 2φ при вершине выделим часть сферической оболочки, как показано на рис. 11.

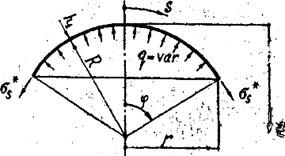
Рис.11. Расчетная схема сферической оболочки

Уравнение равновесия отсеченной части оболочки:

                                              (13)

Осевую равнодействующую P_{z сф}   внешней нагрузки q = var   на рассматриваемую часть оболочки находим по выражению (5), переходя к интегрированию по переменной j:

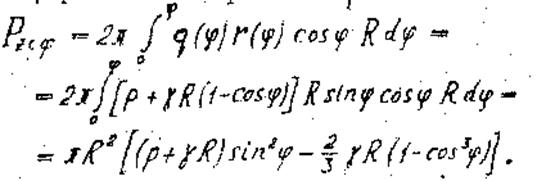                 (14)

Подставляя полученное выражение для P_{z сф}  в уравнение (13) находим меридиональные напряжения в оболочке

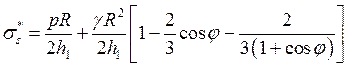 .                                       (15)

Подставляя значения главных радиусов кривизны (11) и выражение (10) для давления q в уравнение Лапласа (3), получаем следующее соотношение:

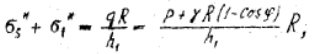                                         (16)

откуда c помощью выражения (15) находим кольцевые напряжения в оболочке:

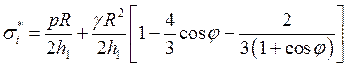.                                    (17)

Радиальные перемещения точек оболочки определяем по формуле (7) с использованием выражений (15) и (17)

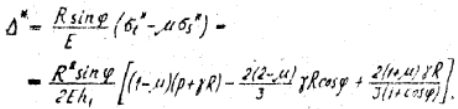                    (18)

Формулу для определения углов поворота нормали к оболочке получим, подставляя соотношение (16) в выражение (8):

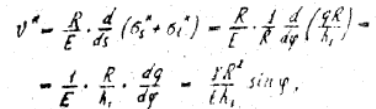                        (19)

6.2. Коническая оболочка

Главные радиусы кривизны конической оболочки:

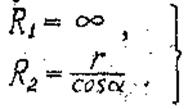                                                    (20)

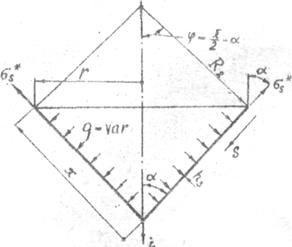
Рис.12.  Расчетная схема конической оболочки.

При расчете конической оболочки удобно ввести параметр x, определяющий расстояние исследуемого сечения от вершины конуса по образующей (см. рис. 10). Радиус параллельного круга и второй главный радиус кривизны конической оболочки выражаются через параметр х  очевидными соотношениями:

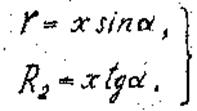                                                  (21)

Внешняя нагрузка изменяется вдоль образующей конуса по закону:

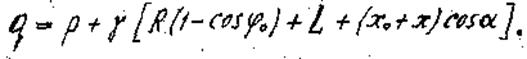               (22)

Кольцевые напряжения в оболочке находим из уравнения Лапласа:

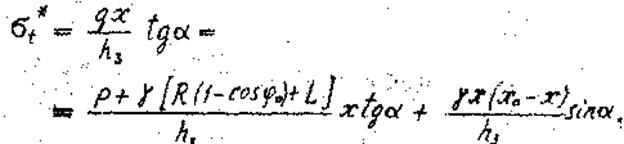      (23)

Меридиональные напряжения находим из уравнения равновесия зоны оболочки, отсеченной нормальным коническим сечением c углом 2j при вершине, (рис.12):

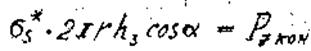                                           (24)

Осевую равнодействующую P_{z кон}   внешней нагрузки на отсеченную часть оболочки, ограниченную параллельным кругом  r = xsin a    (рис. 12)., находим по выражению (5), переходя к интегрированию по переменной х  и принимая во внимание, что cos j = sin a:

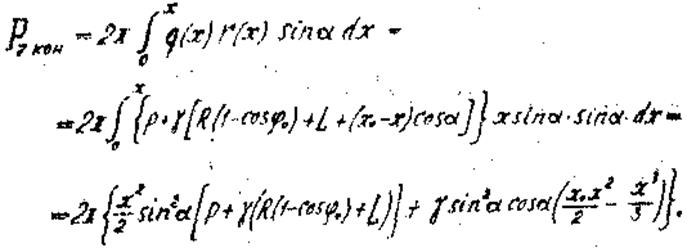       (25)

Подставляя полученное выражение в уравнение (24) находим меридиональные напряжения в оболочке:

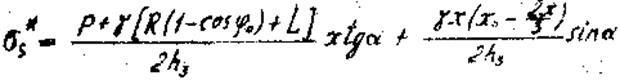              (26)

Радиальные перемещения точек оболочки находим по формуле (7):

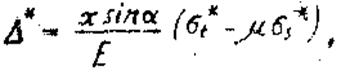                                             (27)

где s_s   и  s_t    определены выражениями (23) и (26).

Угол поворота нормали к оболочке определяем по формуле (8), используя выражения (23) и (26):