Анализ устойчивости и качества процесса управления в линейной непрерывной САУ, страница 5

Устойчивость линейной системы независит от внешних воздействий и начальных отклонений, а зависит только от внутренних свойств системы, т.е от ее параметров.

Внутренние свойства замкнутой системы с точки зрения устойчивости описываются характеристическим уравнением (полиномом)

                              (А.1.5)

Необходимым условием устойчивости является положительность всех коэффициентов полинома

где

Необходимое условие устойчивости выполняется. Оно является также достаточным для замкнутых систем, у которых порядок Для систем, у которых порядок полинома   необходима обязательно проверка достаточного условия устойчивости. Эту проверку в данной работе выполним с помощью Раусса. Составляем таблицу Раусса. Количество строк в таблице Раусса равно , где порядок .

Таблица А.1.1–Значения коэффициентов Раусса

Строка	Столбец
№	1	2	3	4
1
2
3
4
5

По критерию Раусса достаточным условием устойчивости замкнутой системы является положительность всех коэффициентов первого столбца таблицы Раусса . Достаточное условие  выполняется, так как  

А.1.4 Определение установившихся ошибок

Расчет установившихся ошибок начнем с определения порядка астатизма системы по отношению с внешним задающему и возмущающему  воздействиям.

Согласно (А1.2) астатизм системы по отношению к ,так как .

Астатизм системы по отношению к

,т.к. (согласно А.1.3)

А.1.4.1 Расчет установившейся ошибки  по задающему воздействию.

В исходных данных =1(t)+0.5.

Анализ этого выражения позволяет судить о том, что задающее воздействие содержит задание на два типовых движения: неподвижное состояниеи движение с постоянной скоростью поэтому возможно появление двух ошибок: позиционной (статической) и по скорости (кинетической). Но так как порядок астатизма по задающему воздействию , то обе ошибки будут равны нулю, т.е. воспроизведение задающего сигнала будут осуществляться без установившейся ошибки )

А.1.4.2 Расчет установившейся ошибки по возмущающему воздействию.

В исходных данных .Это выражение показывает, что возмущающее воздействие содержит задание на одно типовое движение системы – неподвижное состояние, следовательно, возможно появление позиционной (статической ) ошибки по возмущению.

Поскольку астатизм системы по возмущению ,то статическая ошибка по  не будет равна нулю )

Найдем значение этой ошибки по теореме операционного исчисления о конечном значении оригинала

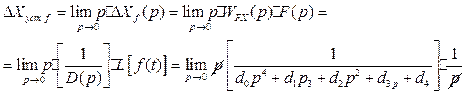
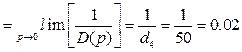                                      (А.1.6)

Суммарная установившаяся ошибка будет равна                           (А.1.7)

А.1.5 Оценка качества переходного процесса

Оценку качества переходного процесса проведем с помощью частотных характеристик, среди которых наиболее популярными являются логарифмические амплитудно  и фазо-частотные характеристики,т.е. ЛАЧХ и ЛФЧХ.

А.1.5.1 Расчет и построение ЛАЧХ

Логарифмическую амплитудно-частотную характеристику рассчитываем по выражению 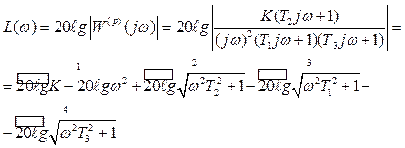      (А.1.8)

У  имеется четыре асимптоты 1, 2, 3 и 4, обозначенные сверху, которые при построении асимптотической ЛАЧХ будут состыкованы между собой на частотах сопряжения

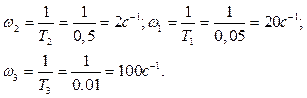
Построение начинаем с нанесения на ось логарифмического масштаба в пределах каждой декады ,а на ось  – равномерного в qБ.

Декада – это отрезок любой длины, заключенный, например между  и 10 , следовательно, отрезок логарифмической оси частот, соответствующий одной декаде, равен

.

В пределах единичного отрезка (см. рис. А.1.2) соответствие между и  представлено таблицей А.1.2

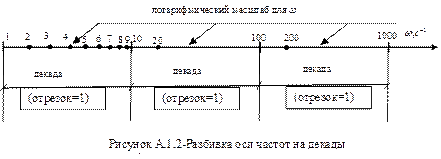
Таблица А.1.2 – Соответствие между  и

	1	2	3	4	5	6	7	8	9	10
	0	0,3010	0,4771	0,6021	0,6990	0,7782	0,8451	0,9031	0,9542	1

Ось ординат для  можно проводить через любую частоту на оси  но всегда левее самой малой частоты сопряжения (для нашего случая левее )

Для точности построения рекомендуется использовать лучевую диаграмму, показывающую наклоны асимптот  на ,,   Проводим  ось L() через частоту Наносим частоты сопряжения ,, и  и строим ЛАЧХ, начиная от первуй и заканчивая последней асимптотой

А.1.5.2  Расчет и построения ЛФЧХ

Фазо-частотная характеристика  строится по выражению (А.1.9)

=-                                                    (А.1.9)

где  – фазовый сдвиг , вносимый числителем комплексной передаточной функции;

 – фазовый сдвиг, вносимый знаменателем .

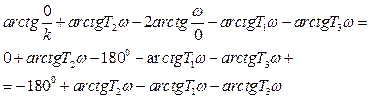
 получаем из (А.1.4),подставляя в него .

Тогда 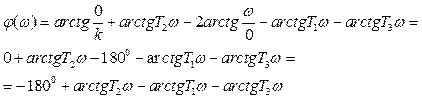  (А.1.10)

 строим по точкам на основании таблицы А.1.3.

 Таблица  А.1.3 – Значений

		1	2	5	10	15	20	50	100	200
	град.	157	142	129	134	144	152	187	197	240

Ось для  совмещаем с осью для, а значение угла
“-180” со значением “0дБ”. Если возникают затруднения с построением асимптотической ЛАЧХ, то можно ее построить по точкам, составив таблицу на основании выражения (А.1.8).

Графики асимптотической ЛАЧХ и  представлены на рисунке А.1.3

Из рисунка А.1.3 находим запасы устойчивости по фазе и по амплитуде дБ.

А.1.6 Анализ полученных результатов

Так как суммарная установившаяся ошибка  и запасы устойчивости вписываются в рекомендуемые значения, то можно сделать вывод о том, что точность работы системы – удовлетворительная и она может эксплуатироваться без коррекции.

Рисунок А.1.3 – Графики ЛАЧХ и ЛФЧХ