Основы корреляционного и регрессионного анализа, страница 5

Значение r всегда лежит между -1 и +1. Знак r такой же, как и знак коэффициента регрессии . По мере того, как возрастает сила линейной связи, точки на графике будут лежать более близко к прямой линии, а величина г будет ближе к 1 или -1. По мере уменьшения силы связи значение r будет ближе к 0, а точки будут более рассеяны. При r=0 линейной связи не существует, т.е. в этом случае может не быть вообще никакой связи или будет нелинейная связь (см. рис.).

Вычислим коэффициент корреляции для исходных данных примера о времени поставок.

.

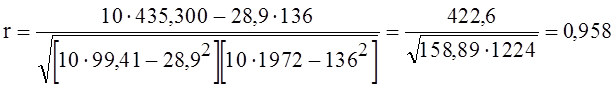Это значение коэффициента очень близко к единице, что говорит об очень тесной линейной связи между расстоянием и временем поставки, что подтверждает наше первоначальное предположение.

Коэффициент детерминации равен

.

Таким образом, линейная модель объясняет 91,8% вариации времени доставки. Не объясняется  вариации времени поездки, которые обусловлены остальными факторами, влияющими на время поставки, но не включенными в модель.

2.6. ОБЗОР СУЩЕСТВУЮЩИХ ЗАДАЧ РЕГРЕССИОННОГО

И КОРРЕЛЯЦИОННОГО АНАЛИЗА

2.6.1. Предсказания и прогнозы на основе линейной модели регрессии

Модели регрессии, полученные путем обработки выборочных данных, могут быть использованы для прогноза значений зависимого параметра Y. Так, например, используя линейную модель регрессии из примера о времени поставок , мы можем предсказать сколько времени в среднем займет поставка груза на расстояние в 4 мили

мин.

(2.11)

Но в расчетах такого рода необходима осторожность, поскольку в РА не рекомендуется использовать модель регрессии для тех значений независимого параметра, которые не принадлежат интервалу, заданному в исходных данных. В нашем примере расстояние в 4 мили входит в исходный интервал от 1,0 мили до 4,9 миль. Но если взять расстояние, например, в 20 миль, то нельзя гарантировать справедливость модели (2.11). Это объясняется тем, что связь между временем и расстоянием может изменяться по мере увеличения расстояния. Например, дальняя поездка может включать использование скоростных шоссе, тогда как наша модель описывала связь с учетом только медленных городских поездок. На время дальних перевозок, кроме того, влияют новые дополнительные факторы, такие как, остановки на отдых, обед.

Поэтому прогнозы для значений независимого параметра, выходящего за пределы собранных экспериментальных данных, являются ненадежными.

2.6.2. Оценка генеральной совокупности

Отдельным направлением РА и КА является анализ того можно ли распространить модель линейной регрессии, полученную после анализа и обработки выборочных исходных данных, на всю генеральную совокупность пар значений параметров X и Y.

Поскольку при построении линейной модели регрессии мы используем данные выборки, то априорно нельзя сказать является ли связь и в генеральной совокупности данных также линейной. Случайная выборка может свидетельствовать о линейности связи параметров, тогда как в действительности в генеральной совокупности связь может быть нелинейной. На рисунке изображены случаи:

n случайной выборки из генеральной совокупности с линейной связью (а) и

n случайной выборки с нелинейной связью (b).

Поэтому разработаны статистические методы, позволяющие определять вероятность того, что линейная связь в выборочной совокупности свидетельствует о линейной связи в генеральной совокупности.

2.6.3. Множественная регрессия

В большинстве случаев исследование позволяет выявить более одного фактора, влияющего каким-либо образом на зависимый параметр. Корреляционная зависимость, описывающая связь между несколькими параметрами, называется множественной. Аналогично, уравнение линейной регрессии вида

называется множественной регрессии. Задача определения численных значений коэффициентов этого уравнения гораздо более сложна и решается с использованием пакетов прикладных программ.

ЛИТЕРАТУРА

1. М.Эддоус, Р.Стенсфилд. Методы принятия решений. - М., Аудит, ЮНИТИ, 1997.

2. В.А. Колемаев, О.В. Староверов, В.Б. Турундаевский. Теория вероятностей и математическая статистика. М., Высшая школа, 1991.

3. В.Е. Гмурман. Теория вероятностей и математическая статистика. М., Высшая школа, 1972.