Нелинейные оптимизационные модели, страница 4

Аналогично вычисляются и остальные частные производные – компоненты градиента.

Для вычисления нового вектора координат сделаем шаг в направлении антиградиента

                                                     (9.5)

С найденным значением Х'' вектора координат вновь вычислим вектор V, значение целевой функции z(Х²) и градиент Ñz(Х²)  в новой точке. Процесс будем продолжать до тех пор, когда все компоненты градиента окажутся с назначенной заранее точностью равными нулю. Равенство градиента нулю означает достижение минимума целевой функции и прекращение дальнйшего поиска.

Множитель l, регулирующий длину шага, можно выбрать различно. Рассмотрим некоторые варианты.

1. Алгоритм приближения к оптимуму малыми шагами. Вычисляем l по формуле 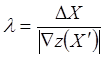, где DХ - малое изменение координат, которым можно пренебречь, а  - модуль градиента.

2. Метод наискорейшего спуска. Назначают l так, чтобы шаг по направлению антиградиента приводил в точку с минимальным значением функции z на данном направлении.

3. Метод Ньютона. Координаты уточняются по формуле

где  - матрица вторых частных производных по параметрам x_i¢ (i = 1, 2, … , k).

Контрольные вопросы

5.  Что такое градиент функции?

6.  Как вычислить градиент функции в заданной точке.

7.  Что такое задача выпуклого программирования?

8.  Что такое градиентный метод поиска экстремума?

9.  Признак достижения максимума при решении задач градиентным методом.

10.  Признак достижения минимума при решении задач градиентным методом.

11.  Выбор направления поиска максимума градиентным методом.

12.  Выбор направления поиска минимума градиентным методом.

13.  Выбор направления поиска при методе наискорейшего подъема.

14.  Выбор направления поиска при методе наискорейшего спуска.

15.  Как вычисляют направление наискорейшего подъема.

16.  Что влияет в градиентном методе на необходимое для достижения максимума целевой функции число шагов приближений?

17.  Что влияет в градиентном методе на необходимое для достижения минимума целевой функции число шагов приближений?

18.  Как уравнять геодезическую сеть, не прибегая к традиционным формулам метода наименьших квадратов?

19.  Что является целевой функцией в методе наименьших квадратов?

20.  Как выполнить уравнивание геодезической сети градиентным методом поиска экстремума? 

21.  Каким методом можно уравнять геодезическую сеть так, чтобы минимизировать сумму модулей поправок к результатам измерений?

9.5. Решение задачи выпуклого программирования с линейными ограничениями

Если целевая функция  имеет экстремум внутри допустимой области, то решение задачи находим теми же методами, какие рассмотрены в разделах 9.2 и 9.3.

Если экстремум функции  находится вне допустимой области, то экстремальное в пределах допустимой области значение надо искать на границе области.

Пусть целевая функция  - вогнутая. Тогда задача выпуклого программирования с линейными ограничениями имеет вид:

max z = f(x)                                                                                   (9.6)

                                                                                         (9.7)

                                                                                              (9.8)

где  = (x₁; x₂; … ; x_n) и  = (a_i1; a_{i 2}; … ; a_{i n}).

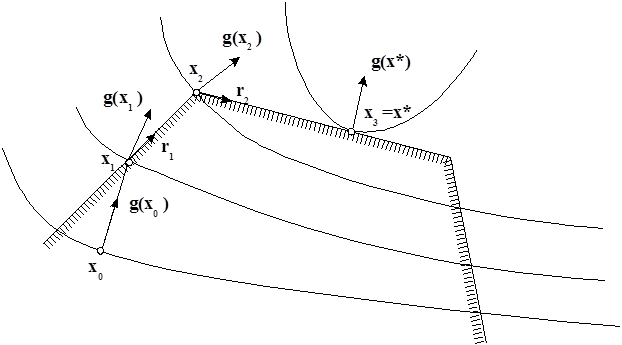
Наметим план решения задачи (см. рис.)