Линейное программирование, Элементы сетевого планирования и теории игр

Переход от одного опорного плана к другому, значение целевой функции в котором больше, чем в предыдущем.

3.  Проверка оптимальности полученного плана, позволяющая своевременно остановить перебор опорных планов или сделать вывод об отсутствии оптимального плана.

Симплекс - метод основан на следующих теоремах, которые приводятся без доказательства.

Теорема 1.2 (о существовании опорного плана)

Если линейная форма ограничена сверху на непустом множестве D, то ЗЛП разрешима, то есть существует такая точка , что .

Теорема 1.3 (признак оптимальности опорного плана)

Опорный план  задачи (1.18) является оптимальным, если для всех j ,  выполняется, где величина

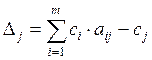                                                   (1.21)

называется симплекс – разностью или оценкой.

Теорема 1.4 (признак отсутствия оптимального плана)

Если  при некотором k и среди чисел ,  нет положительных, т.е. все , целевая функция задачи не ограничена на множестве допустимых решений и не имеет конечного решения.

Теорема 1.5 (признак существования лучшего опорного плана)

Если опорный план  задачи (1.18) не вырожден и  для некоторых k, но среди чисел ,  есть хоты бы одно положительное, т.е. не все , то существует опорный план , в котором целевая функция принимает значение не меньше, чем в предыдущем плане: .

Алгоритм симплекс-метода

1.  Задача должна быть приведена к каноническому виду. Система ограничений приведена к единичному базису, т.е. разрешена относительно некоторых базисных переменных (не умоляя общности, будем считать, что относительно первых m переменных) с помощью метода Жордана – Гаусса (система (1.19)). Получено соответствующее исходное опорное решение .

2.  Для удобства ведения вычислений записываем все в симплекс-таблицу (табл. 1.1). Столбец «Базис» содержит список базисных переменных; следующий столбец «c_j базиса» содержит коэффициенты целевой функции при базисных переменных; следующие столбцы содержат коэффициенты системы ограничений при соответствующих переменных; столбец «b_i» - столбец свободных членов системы ограничений. Последняя строка содержит симплекс – разности, рассчитанные по формуле (1.21) и последняя ячейка содержит значение целевой функции =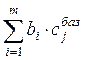. Отметим, что симплекс – разности базисных переменных всегда равны нулю.

Таблица 1.1

3.  Если все симплекс – разности неотрицательны, т.е. , то опорный план оптимален.

4.  Если хотя бы одна симплекс – разность отрицательна, , и в соответствующем столбце нет положительных элементов, то задача не имеет оптимального решения, т.е. .

5.  Если хотя бы одна симплекс – разность отрицательна, , и в каждом столбце, имеющем отрицательную оценку, есть хотя бы один положительный элемент, то полученный опорный план можно улучшить.

6.  Выбираем разрешающий столбец «р», которому соответствует наименьшая отрицательная оценка.

7.  Выбираем разрешающую строку «к», которой соответствует наименьшее из отношений правых частей к соответствующим положительным элементам разрешающего столбца . Элемент, стоящий на пересечении разрешающего столбца и разрешающей строки называется разрешающим элементом.

8.  Переходим к новой симплекс – таблице, в которой будет новый базис: базисная переменная на «к» - ом месте в старом базисе меняется на новую переменную . Соответствующий вектор новой базисной переменной нужно превратить в единичный. Для этого разрешающую строку делим на , чтобы на месте разрешающего элемента появилась единица. Умножая разрешающую строку на подходящие числа и складывая её с остальными строками получаем нули в разрешающем столбце. После этого выписываем новый опорный план и пересчитываем строчку оценок. Переходим к пункту 3.

Замечание об альтернативном плане.

Если все оценки свободных переменных в последней симплекс – таблице окажутся строго больше нуля, то оптимальный план единственен. В случае если хотя бы одна оценка при свободной переменной окажется равной нулю, то имеет место альтернативный оптимум (множество оптимальных планов). Чтобы найти альтернативное решение, необходимо сделать один шаг симплекс-метода, выбрав в качестве разрешающего столбец свободной  переменной, которому соответствует нулевая оценка.

В этом случае множество все оптимальных планов можно представить в виде выпуклой линейной комбинации опорных оптимальных планов: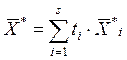, где .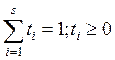

Пример 5. Решить ЗЛП симплекс-методом:

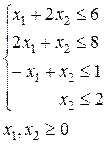                                               (1.22)

Приводим систему линейных неравенств  (1.22) к каноническому виду, вводя в каждое неравенство дополнительную неотрицательную переменную. Получим систему линейных уравнений:

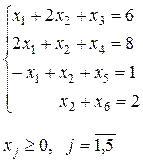                                       (1.23)                  

Целевая функция будет иметь вид

.

Составляем симплекс – таблицу:

Таблица 1.2

Опорный план  не является оптимальным, т.к. в строке оценок есть отрицательные элементы  = - 3 и  = - 2. Выбираем разрешающий столбец – первый, т.к. ему соответствует минимальная из отрицательных оценок  = - 3. Для всех положительных элементов первого столбца вычисляем отношение . Находим минимальное из этих отношений: 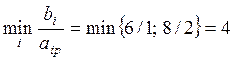. Оно соответствует второй строке, следовательно, она будет разрешающей. Таким образом, разрешающий элемент  показывает, что из базиса выводится переменная x₄, а вместо неё в базисе будет переменная x₁. Заполняем новую симплекс – таблицу (табл. 1.3). Для этого превращаем первый столбец в единичный. Умножаем вторую строку на (-1/2) и складываем с первой, записываем результат в первую строку новой симплекс – таблицы; аналогично, умножаем вторую строку на (1/2) и складываем с третьей;  разрешающую строку делим на 2; четвертую переписываем без изменений.

 Таблица 1.3

Заполняем строку оценок: , как базисные; ;

;

.

Получили новое опорное решение , которое тоже не является оптимальным, т.к. есть отрицательная оценка  = -1/2. Его можно улучшить, выбрав второй разрешающий столбец и первую