Задача о конях. "Какое максимальное количество коней можно расставить на шахматной доске так, чтобы они не били друг друга".

Министерство образования и науки Российской Федерации

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра прикладной математики и информатики

Лабораторная работа №2

Факультет:                     ПМИ

Группа:                            ПМ-15

Студенты:                       Голубева М. В.

Кичаева Н. А.

Вариант:                          2

Преподаватели:             Пономаренко В.М.

Ванюкевич О.Н.

Новосибирск

2005

1.  Цель работы:

Задача о конях. "Какое  максимальное  количество коней можно расставить на шахматной доске так, чтобы они не били друг друга".

2.  Задание

1.  Сформулировать задачу в закрытой форме. Выбрать комбинацию из следующих подходящих стратегий решения задачи:

-  представление в пространстве состояний;

-  сведения задач к подзадачам;

-  генерация вариантов и проверка;

-  поиск в глубину с возвратом;

-  поиск в ширину;

-  поиск с предпочтением (эвристический поиск),

-  распространение ограничений;

-  сведение задачи к доказательству теоремы.

2.  Разработать адекватную структуру данных, максимально учитывающую специфику  предметной области задачи. Обосновать выбор структуры.

3.  Реализовать формальное описание проблемы на Прологе, снабдив программу достаточным количеством средств ввода - вывода для наглядного отображения результатов.

4.  В режиме трассировки пронаблюдать стратегию обхода "И-ИЛИ" - дерева решения задачи.

5.  Выделить пространство состояний и нарисовать граф переходов.

6.  Привести интерпретацию программы с точки  зрения декларативной и процедурной семантик.

7.  Еще раз вернуться к постановке задачи и попробовать написать "максимально  декларативный" вариант  программы на Прологе, т.е. взглянуть на проблему аксиоматически, считая, что решение  задачи - это конструктивное доказательство теоремы в рамках некоторой формальной теории, задаваемой системой аксиом. Все внелогические предикаты типа ввода-вывода и пр. вынести за рамки формулировки задачи.

3.  Реализация

Сформулируем преложенную задачу в терминах пространства состояний:

• Вершины пространства состояний – позиции, в которых представлено несколько (возможно, 0) коней, расположенных некотором допустимом порядке на шахматной доске (ни один из них не бьет другого).
• Вершина-преемник из данной вершины может быть получена после того, как на шахматную доску будет добавлен еще один конь, причем таким образом, чтобы он не бил ни одного из уже находящихся на доске коней.

Алгоритм решения задачи – поиска в глубину.

Наглядно пространство состояний может быть представлено в виде:

Алгоритм поиска решения полнопереборный и с увеличением числа коней, которых необходимо расставить на доске, количество перебираемых вариантов сильно возрастает.

Максимальное число коней, которых можно разместить на доске 8х8, составляет 32.

Правильный алгоритм расстановки коней(имеется ввиду самый эффективный) заключается в том, чтобы расставлять так, чтобы по вертикали и по горизонтали кони были друг от друга через одну, а соседствовали только по диагонали.

Аналогично тому, как это было сделано для задачи о восьми ферзях в книге

“И.Братко Программирование на языке ПРОЛОГ для искусственного интеллекта”, для реализации алгоритма сформулируем необходимые условия

Для отношения решение

a)  Кони, перечисленные в списке остальные не должны бить друг друга, т.е. сам список oстальные должен являться решением.

b)   X и Y должны быть целыми числами от 1 до 8 (доска 8х8)

c)  Конь, стоящий на поле X\Y, не должен бить ни одного коня из списка остальные.

Если список коней пуст то он является решением.

Добавим однако еще в предикат решение в качестве параметра количество коней которых еще надо разместить на доске.

Решение([], []).

Решение([X|остальныеХ], [Y|остальныеY]):-

    Решение(остальныеХ, остальныеY),

    Принадлежит(Х,[1,2,3,4,5,6,7,8]),

    Принадлежит(Y,[1,2,3,4,5,6,7,8]),

    Небьет(Х, Y, остальныеХ, остальныеY).

Теперь определим отношение небьет(Х, Y, СписХ, СписY)

Здесь список СписХ = [Х1|СписХ1]  Спис =[Y1|СписY]

a)  Если список пуст то отношение выполнилось т.к. некого бить

b)  Если список не пуст то должно выполняться что

·  Х/Y не должен бить ни одного коня из списка остальные

·  Х/Y не должен бить Х1/Y1

Данные условия  выражаются следующим предикатом

Небьет(_,_,[],[]).

Небьет(Х, [Х1|СписХ],[Y1|СписY]):-

     Неравны(Х ,Х1,Y,Y1),

     Небьет(X,Y,СписХ, СписY)

     Не( Бьет(Х, Y, Х1, Y1))

Предикат бьет() просто проверяет не выполняется какая-нибудь из следующих ситуаций

4.  Текст программы

domains

list=integer*

predicates

solution(integer,list,list);

solve(integer,integer,list,list);

nottake(integer,integer,list,list);

belong(integer,list);

take(integer,integer,integer,integer);

run    

clauses

run:clearwindow,

write("Menu:"),nl,

write("Choose 1 to set number of knights."),nl,

write("Choose 2 to use the best strategy from the begining."),nl,

readint(S),

S=1,

write("Enter number of Knights : "),

readint(N),

solution(N,X,Y),

write(X),

write("\n"),

write(Y).

run:S=2,

write("The best strategy is to set knights in 1!"),nl,

N=0,

solve(N,1,[1],[1]).

solution(0,[],[]).

solution(N,[X|XS],[Y|YS]):N>0,

N1=N-1,

solution(N1,XS,YS),

belong(X,[1,2,3,4,5,6,7,8]),

belong(Y,[1,2,3,4,5,6,7,8]),

nottake(X,Y,XS,YS).

nottake(_,_,[],[]).

nottake(X,Y,[A|XTAIL],[B|YTAIL]):-

X>A,

nottake(X,Y,XTAIL,YTAIL),

not(take(X,Y,A,B)).

nottake(X,Y,[A|XTAIL],[B|YTAIL]):-

X=A,

Y>B,

nottake(X,Y,XTAIL,YTAIL),

not(take(X,Y,A,B)).

take(X,Y,A,B):- A=X+1, B=Y+2.

take(X,Y,A,B):- A=X-1, B=Y+2.

take(X,Y,A,B):- A=X+1, B=Y-2.

take(X,Y,A,B):- A=X-1, B=Y-2. 

take(X,Y,A,B):- A=X+2, B=Y+1.

take(X,Y,A,B):- A=X-2, B=Y+1.

take(X,Y,A,B):- A=X+2, B=Y-1.

take(X,Y,A,B):- A=X-2, B=Y-1.

belong(Y,[Y|L]).

belong(Y,[Z|L]):-belong(Y,L).

solve(N,M,[X|XS],[Y|YS]):X1=X+2,

belong(X1,[1,2,3,4,5,6,7,8]),

N1=N+1,

solve(N1,M,[X1,X|XS],[Y,Y|YS]).

solve(N,M,[X|XS],[Y|YS]):M=1,

X1=2,

Y1=Y+1,

belong(Y1,[1,2,3,4,5,6,7,8]),

N1=N+1,

M1=2,

solve(N1,M1,[X1,X|XS],[Y1,Y|YS]).

solve(N,M,[X|XS],[Y|YS]):M=2,

X1=1,

Y1=Y+1,

belong(Y1,[1,2,3,4,5,6,7,8]),

N1=N+1,

M1=1,

solve(N1,M1,[X1,X|XS],[Y1,Y|YS]).

solve(N,_,XS,YS):write("The max number of knights is:"),

N1=N+1,

write(N1),nl,

write("X coordinates:"),

write(XS),

write("\n"),

write("Y coordinates:"),

write(YS).     

goal

run. 

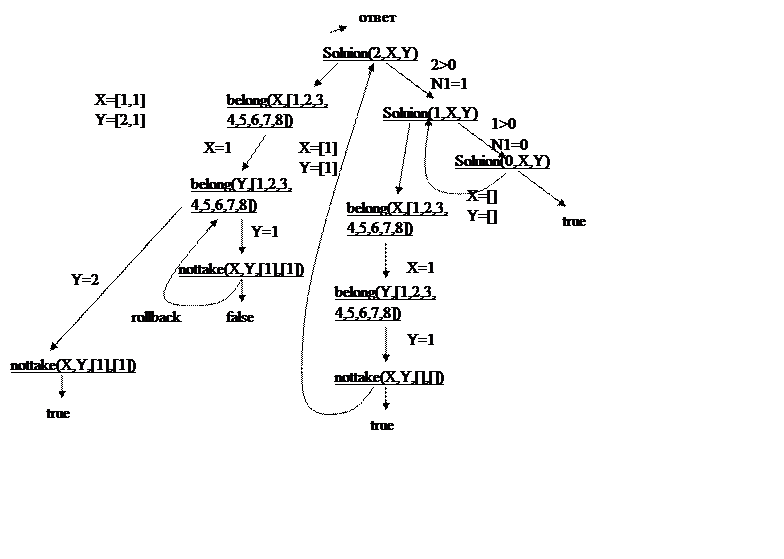
Рассмотрим для примера дерево решения при  S=1 (для переборного алгоритма) и числу коней N=2: