Синтез оптимального управления на основе вариационного исчисления, страница 2

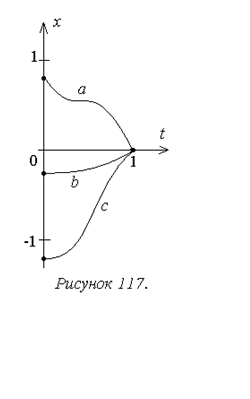
Пример 2. Требуется обеспечить экстремум функционала  при граничном условии x(1)=0 (рисунок 117).

В данной задаче левый конец подвижен. Поэтому потребуется составить и учесть одно условие трансверсальности вида (24.5).

Найдем частные производные и составим уравнение Эйлера и условие трансверсальности:

, ;

, ;

.

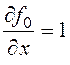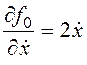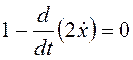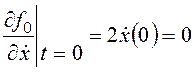Получим уравнение экстремали: , .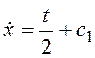

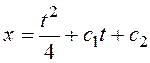С учетом условия трансверсальности и граничного условия находим допустимую экстремаль: , , , .

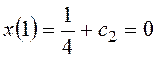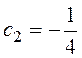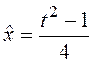Проверим выполнение условия Лежандра: .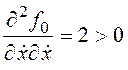

Таким образом, на кривой 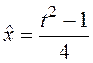 (кривая bна рисунок 117) обеспечивается минимум величиной .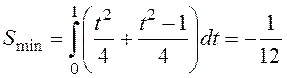

В вариационных задачах на условный экстремум на функцию X, помимо граничных условий, накладываются дополнительные ограничения в форме некоторых уравнений (уравнений связи) или неравенств. Такие задачи наиболее часто распространены на практике. Так в задачах синтеза систем управления такими уравнениями являются уравнения объекта управления.

Наиболее просто учитываются ограничения в форме уравнений. Здесь аналогично задачам на достижение условного экстремума функции применяется принцип неопределенных множителей Лагранжа, развитый с учетом разновидностей уравнений связи в вариационных задачах. Общий подход состоит в том, что задача на условный экстремум функционала вида (24.3) сводится к задаче на безусловный экстремум нового функционала

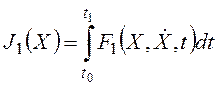,                                       (24.8)

причем вид функции F₁ (функции Лагранжа) зависит от вида уравнений связи.

Рассмотрим основные виды таких задач.

Задача Лагранжа (задача с дифференциальными связями): требуется обеспечить экстремум функционала 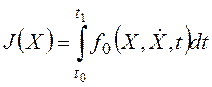 при граничных условиях x_i(t₀)=x_i0, x_i(t₁)=x_i1, i=1,2,...,n причем допустимые кривые должны удовлетворять уравнениям связи

,  j=1,2,...m<n.                              (24.9)

Функция Лагранжа в задаче Лагранжа вводится следующим образом:

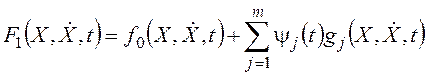, где y_j(t) - произвольные функции времени, выступающие здесь как аналог неопределенных множителей Лагранжа в задаче обеспечения экстремума функции.

Экстремум функционала (24.8) ищут на основе рассмотренной выше системы необходимых и достаточных условий, причем при поиске допустимых экстремалей здесь возникает ситуация, когда имеется n+m неизвестных функций: x_i(t), i=1,2,...,n и y_j(t), j=1,2,...,m. Для их нахождения имеются m уравнений связи, а также n уравнений Эйлера-Лагранжа, составляемых дифференцированием функции F₁. Отметим, что для получения результата функции y_j находить, вообще говоря, не требуется, и в ряде конкретных задач их удается исключить в ходе решения.

Условия трансверсальности и Лежандра также применяются к функции F₁.

Пример 3. Требуется обеспечить экстремум функционала  при граничных условиях x₁(0)=0, x₂(0)=1 с учетом уравнения связи .

Составим функцию Лагранжа: .

Найдем частные производные и составим систему уравнений Эйлера-Лагранжа и необходимые условия трансверсальности (левый конец в задаче закреплен, правый подвижен):

, , , ;

,

;

, .

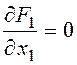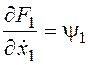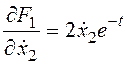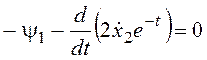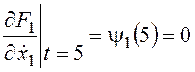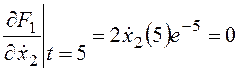Интегрированием полученных уравнений получим: y₁=c₁,  .

Применив условия трансверсальности, получим c₁=0, c₂=0 и .

Последовательно интегрируя последнее полученное уравнение и уравнение связи, получим уравнения экстремали: x₂=c₃, x₁=c₃t+c₄.

С учетом граничных условий находим допустимую экстремаль: , .

Составим матрицу частных производных и проверим выполнение условия Лежандра:

,  D₁=D₂=0.

Вывод о характере экстремума сделать не удается. Тем не менее, с учетом неотрицательности интегранта значение функционала, доставляемое найденной допустимой экстремалью J=0, очевидно, является минимумом.

Таким образом, на кривой  обеспечивается минимум величиной S_min=0.

Изопериметрическая задача (задача с интегральными связями): требуется обеспечить экстремум функционала 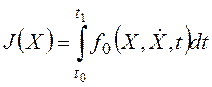 при граничных условиях x_i(t₀)=x_i0, x_i(t₁)=x_i1, i=1,2,...,n причем допустимые кривые должны удовлетворять уравнениям связи в форме интегральных уравнений:

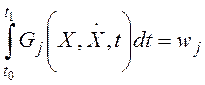,  j=1,2,...k.                             (24.10)

Отметим, что в отличие от задачи Лагранжа, количество уравнений связи здесь не ограничено.

Функция F₁ вводится в данной задаче непосредственно в соответствии с принципом неопределенных множителей Лагранжа:

, где l_j - произвольные постоянные коэффициенты.

Если в задаче одновременно присутствуют уравнения связи вида (24.9) и (24.10), функция F₁ вводится в форме:

 .

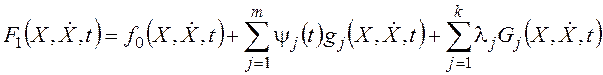Для нахождения экстремума функционала к функции F₁ применяются условия (24.4)-(24.7) с учетом размерности задачи и полноты граничных условий.