Математика \ Математика

Дифференциал и интеграл булевой функции, страница 4

___________         = f (xl,x2,...,xn) v f (xl,x2,...,xn) = f (xl,x2,...,xn);

∂xn+1          v 

∂ (f (xl,x2,...,xn) & хn+1)

__________________           = 0 v f (xl,x2,...,xn) = f (xl,x2,...,xn);

∂xn+1                                  v   

                                           _                                                                                                                                          

∂ (f (xl,x2,...,xn) & хn+1)

___________________            = f (xl,x2,...,xn) v 0= f (xl,x2,...,xn).

∂xn+1                       v 

Дальнейшие исследования показали, что для функций, содержащих две коституэнты, т. е. принимающих значение 1 в двух точках пространства, количество интегральных функций равно 9; в трех — 27 и так далее независимо от размерности пространства n. Из этого заключаем, что количество интегральных функций по операции дизъюнкция зависит от вида самой подынтегральной функции следующим образом:

3k , где k – количество единиц (конституэнт) функции.

На основании проведенных исследований для функций различной сложности в пространстве различной размерности запишем общий вид интеграла для булевой функции по операции дизъюнкция:

          m

∫  V fi (xl,x2,...,xn)dx n+1 = f1 (xl,x2,...,xn) & x σ1 n+1 v f2 (xl,x2,...,xn) & x σ2 n+1 v…

     v  i=1

m                                                                                                                                          

v                                                                                                                                          

… v fm (xl,x2,...,xn) & x σm n+1 = ∑  fi (xl,x2,...,xn) & x σi n+1 ,

i =1

A (σ1, σ2, …, σm)

_                                                                                                                                           

(   x n+1 ,                     если σi = 0;

где x σi n+1 =  {   x n+1 ,                     если σi = 1; и σi = {0, 1, 2} – все возможные

_                                                                                                                                           

(   (x n+1  v x n+1) = 1, если σi = 2

различные комбинации, отметив следующую очевидную закономерность: все имеющиеся в представлении функции конституэнты поочередно

_                                                           _                                                                                                                                           

«домножаются» сначала на xn+1, затем на хn+1, и, наконец, на xn+1 v xn+1 = 1.

Очевидно, что если две функции f1 и f2 различны, то соответствующие им множества интегральных функций также абсолютно различны, так как дифференциал интегральной функции по переменной            xn+1 дает нам саму эту функцию. Отсюда следует, что мощность объединения множества логических функций интегралов от всех логических переменных от n переменных для операции дизъюнкция равна количеству всех логических функций от n + 1 переменных, т. е. два в степени два в степени n + 1. Действительно, проверено, например, что количество интегральных функций для всех функций от двух переменных (n = 2) по операции дизъюнкция равно 256, то есть =.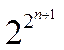

Исследование интегралов для операций конъюнкция и «сложение по модулю 2» проводилось аналогично. Было замечено, что количество интегральных функций для операции конъюнкция зависит не от количества конституэнт, а от количества «нулей» в функции и равно 3кн, где кн – количество нулей функции.

Общий вид интегральных функций для операции конъюнкция формируется следующим образом: все имеющиеся в представлении функции                                                                                       

_                                                                                                                                           

Скачать файл