Моделирование непрерывных случайных величин, заданных графиком: Отчёт по компьютерному практикуму "Генераторы непрерывных случайных величин", страница 2

Необходимо оценить возможную при этом ошибку. Назначим некоторую достаточно большую вероятность β (в случае практикума, β = 0.95), такую, что событие с вероятностью β можно считать практически достоверным, и найдем такое значение e, для которого

                                                    (7)

Данное равенство означает, что с вероятностью β неизвестное значение параметра a попадает в интервал

,                                                    (8)

диапазон наиболее вероятных значений ошибки, возникающих при замене a на  по модулю не будет превосходить e. Большие по абсолютной величине ошибки будут появляться с малой вероятностью α = 1 - β.                            

Необходимо отметить, что в данном случае величина a не случайна, но случаен интервал I. И величину β можно трактовать как вероятность того, что случайный интервал I накроет истинное значение параметра a. Вероятность β называют доверительной вероятностью, интервал I - доверительным интервалом, а  называют доверительными границами.

Если бы была известна функция распределения случайной величины  (или ее плотность распределения вероятности), то задача нахождения доверительного интервала была бы весьма проста: достаточно было бы найти такое значение e, для которого выполняется условие (6). Трудность состоит в том, что функция распределения оценки  зависит от функции распределения величины Х и, следовательно, от самого неизвестного параметра a. Для β=0.95, параметр t=1.96, на его основе и рассчитывается доверительный интервал.

Рассчитаем его для нашей последовательности дискретных величин средствами среды MatLab:

mu2=sum/N;

t=1.96;

sigma=realsqrt(d/N);

disp('Среднеквадратичное отклонение:');

disp(sigma);

e=t*sigma;

I(1)=mu2-e;

I(2)=mu2+e;

disp('Доверительный интервал:');

disp(I);

При данной вероятности β=0,95 и сгенерированной последовательности дискретных величин получаем доверительный интервал (4.1114    4.3213)

5. Также качественными характеристиками последовательности вероятностных чисел являются ковариационная и корреляционная функции. Для оценки корреляционной функции полученной последовательности по графикам (j, ρ(j)) и (Xj, Xj + 1), необходимо сначала произвести оценку ковариационной функции по формуле:

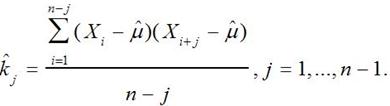                            (9)

А затем рассчитать оценку корреляционной функции по формуле:

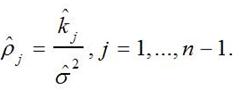                                              (10)

Реализуем данную задачу в системе Matlab (для первых ста элементов последовательности):

%Оценка ковариационной функции:

for j=1:N-1

    sum3=0;

    for i=1:(N-j)

        sum3=sum3+(x(i)-mu)*(x(i+j)-mu);

    end;

    k(j)=sum3/(N-j);   

end;

%Оценка корреляционной функции:

for j=1:N-1

    p(j)=k(j)/d;

end;

Графическое представление корреляционной функции можно увидеть на рисунке 5:

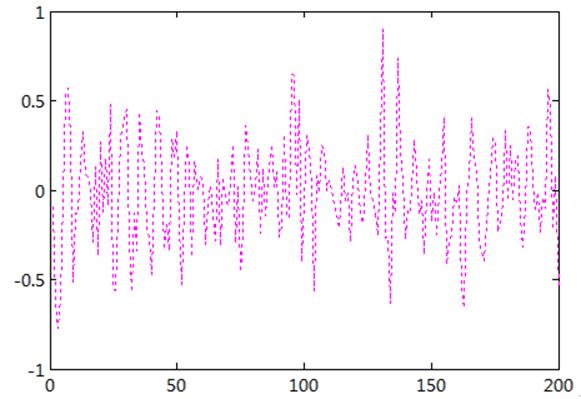
Рис. 5. Оценка корреляционной функции первых 200 случайных величин.

Корреляция — это статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Исследуя график корреляционной функции, мы видим, что аппроксимация приводит к получению прямой y=0, то есть  величины относительно независимы друг от друга. 

На фазовой диаграмме зависимости следующего элемента от предыдущего для первых 100 элементов последовательности (рис. 6) не имеют место явно заметные зависимости, то есть каждый следующий элемент последовательности можно условно назвать независимым от предыдущего.

Рис. 6. График зависимости X_j+1 от X_j первых 100 случайных величин.

6. Гипотезу о законе распределения методом гистограмм, проверяем построением гистограммы, представленной на рисунке 7:

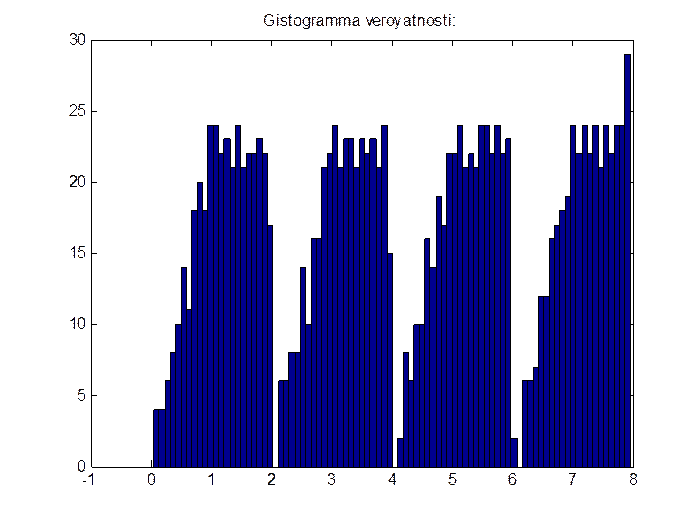
Рис. 7. Гистограмма распределения вероятности генерации случайных величин.

Построенная гистограмма свидетельствует о том, что заданная таблица распределения полностью обеспечивается данным методом моделирования генератора последовательности непрерывных величин. 

ЗАКЛЮЧЕНИЕ

Анализ модели генератора непрерывных случайных величин приводит к выводу, что использование конгруэнтного линейного генератора для этой цели обеспечивает заданные требования к распределению вероятностей появления величин в последовательности, и при этом даёт близкую к нулю корреляцию последовательности, что означает независимость элементов друг от друга, обеспечивая «псевдослучайную» генерацию.

ПРИЛОЖЕНИЕ 1

Ниже приведён листинг кода на языке MatLab 7.0, реализующего программу экспериментальных исследований, содержащую в себе решение поставленных задач:

%определение параметров

a=17;

c=3;

m=1024;        

x(1)=10;

y(1)=500;

num=2000;      

%генерация и вывод последовательности

disp('Последовательность случайных чисел по методу Лемера: ');

for i=2:num

    x(i)=mod(a*x(i-1)+c,m);

    y(i)=mod(a*y(i-1)+c,m);

end;

for i=1:num

    x(i)=x(i)/m*8;

    y(i)=y(i)/m*0.25;

end;

N=0;

sum=0;

xx=0;

for i=1:num

    if x(i)<=2

        if x(i)>4*y(i)

            N=N+1;

            xx(N)=x(i);

            disp(xx(N));

            sum=sum+xx(N);

        end;

    elseif x(i)>=2.01&x(i)<=3.99

        if x(i)>4*y(i)+2;

            N=N+1;

            xx(N)=x(i);

            disp(xx(N));

            sum=sum+xx(N);

        end;

            elseif x(i)>=4&x(i)<=5.99

        if x(i)>4*y(i)+4;

            N=N+1;

            xx(N)=x(i);

            disp(xx(N));

            sum=sum+xx(N);

        end;

            elseif x(i)>=6&x(i)<=8

        if x(i)>4*y(i)+6;

            N=N+1;

            xx(N)=x(i);

            disp(xx(N));

            sum=sum+xx(N);

        end;

    end;

end;

%вывод последовательности

figure (1);

plot(xx,'y');

axis auto;

title(' Sgenerirovannya posledovatelnost sluchainyh chisel: ');

%оценка мат. ожидания

disp('Оценка мат. ожидания: ');

mu=sum/N;

disp(mu);

%оценка дисперсии

disp('Оценка дисперсии: ');

sum2=0;

for i=1:N

    sum2=sum2+(xx(i)-mu)^2;

end;

d=sum2/N-1;

disp(d);

%Оценка ковариационной функции:

%disp('Оценка ковариационной функции для первых 20 элементов: ');

for j=1:N-1

    sum3=0;

    for i=1:(N-j)

        sum3=sum3+(xx(i)-mu)*(xx(i+j)-mu);

    end;

    k(j)=sum3/(N-j);   

    %disp(k(j));

end;

%Оценка корреляционной функции:

%disp('Оценка корреляционной функции для первых 20 элементов: ');

for a=1:N-1

    p(j)=k(j)/d;

    %disp(p(j));

end;

%построение графика зависимости элементов

figure (2);

j=1:100;

plot(x(j),x(j+1), '-r');

title(' Ozenka zavisimosti predidujego elementa ot sleduyujego: ');

%построение графика оценки корреляционной функции

figure (3);

j=1:200; plot(j,p(j), ':m');

title(' Ozenka korrelyazionnoy funkzii: ');

%оценка доверительного интервала

mu2=sum/N;

t=1.96;

sigma=realsqrt(d/N);

disp('Среднеквадратичное отклонение:');

disp(sigma);

e=t*sigma;

I(1)=mu2-e;

I(2)=mu2+e;

disp('Доверительный интервал:');

disp(I);

%исследование методом гистограмм

h=0:0.09:8;

figure (4);

hist(xx,h);

title(' Gistogramma veroyatnosti: ');

axis auto;