Каскад атомных столкновений (элементарная теория)

Лекция 9

1. Каскад атомных столкновений (элементарная теория)

На этой лекции мы рассмотрим, как первичный атом отдачи образует смещенные атомы, а те, в свою очередь другие, в результате чего развивается каскад атомных столкновений.

Основоположники теории каскадов атомных столкновений ввели так называемую каскадную функцию n(E₂), которая дает среднее число смещенных атомов, образованных атомом отдачи с энергией Е₂.

На предыдущих нескольких лекциях для падающего потока излучения мы научились получать эффективное дифференциальное сечение dσ. Образование первичного атома отдачи с энергией в интервале от Е₂ до Е₂ + dЕ₂ и соответствующую плотность вероятности Р(Е₂).

Мы указали точный способ и рассмотрели приближенные способы решения задачи.

Связь между dσ и Р(Е₂) следующая:

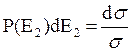,                                           (9.1)

или 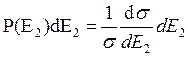                                                                                                (9.2)

Для жёстких сфер, т.е для короткодействующего потенциала мы получили 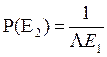 (константу или “ступеньку”). Для других видов потенциала справедливы приближения в виде различных степенных функций.

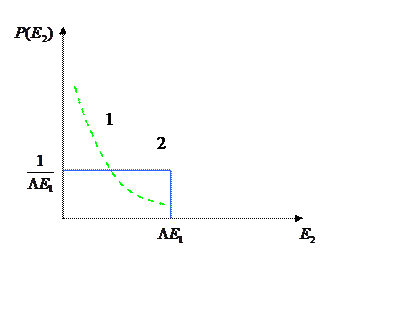
Рис. 9.1. Типичный вид зависимостей Р(Е₂)  для дальнодействующего (1) и короткодействующего (2) потенциалов.

С учетом (9.1), (9.2) очевидно, что, если мы имеем поток бомбардирующих частиц F(см^-2,с^-1), а облучение продолжается t секунд, то атомная концентрация, смещенных атомов, даётся соотношением:

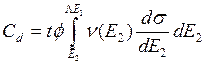        (, см^-2 –флюенс, доза)                    (9.3)

Действительно, (9.3) может быть записано, как

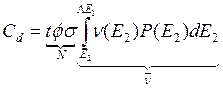,                                                 (9.4)

где N – число образованных атомов отдачи, а  - среднее число атомов , смещенных одним атомом отдачи независимо от его энергии (т.е. усреднённое по всем энергиям).

С целью уяснения некоторых свойств (или параметров) атомных каскадов рассмотрим простейший метод расчёта каскадной функции предложенной Кинчиным и Пизом (1955г).

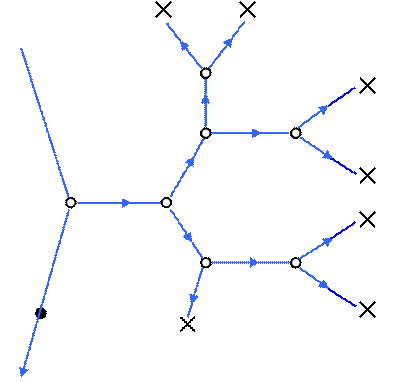
· - налетающая частица

○ - вакансия

× - междоузлие

атомы отдачи и рассеянные атомы

Рис. 9.1. Схема развития каскада атомных смещений.

Кинчин и Пиз сделали следующие исходные допущения:

1)  атомы (частицы) при соударении ведут себя как твёрдые (жёсткие) сферы;

2)  все соударения упругие - и на возбуждение электронов энергия не расходуется;

3)  каскад - последовательность соударений двух тел (т.е. соударения парные);

4)  соударения независимые (пространственные корреляции, связанные с периодичностью структуры не учитываются);

5)  если атом с энергией E рассеивается с энергией E’, образуя атом отдачи с энергией E’’, то E = E’+E” , т.к. энергия решетке не передается;

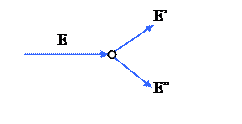
6)  атом, покоившийся до столкновения и получивший энергию меньше некоторой критической E”< E_d (где E_d – это энергия смещения атома), не смещается; аналогично, если энергия рассеянного атома после соударения E’< E_d , то он также не даёт вклад в каскад;

7)   предполагается что энергия E_d константа, т.е. одинакова для всех атомов и изотропна (не зависит от направления);

В настоящее время известно, что предположение об изотропии E_d не выполняется (Рис.9.2), однако, оно может быть использовано для получения грубых оценок.

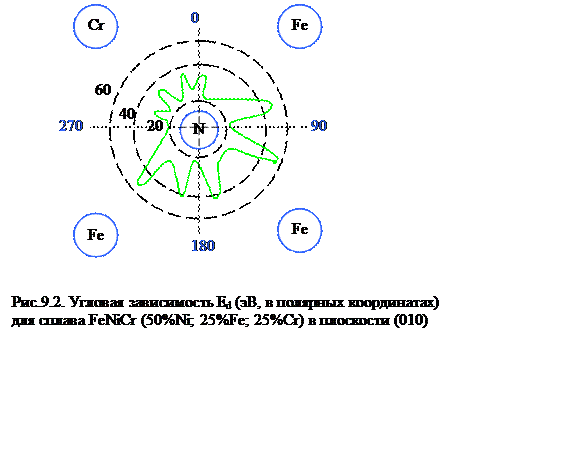ГЦК – решётка

20 ≤ E_d ≤ 60 (эВ)

Кинчин и Пиз считали, что критическая энергия E_d = const и что вероятность смещения равна нулю для E < E_d и резко возрастает до единицы при E = E_d.

          Кроме того, из предположения 6) следует, что атом, для которого E_d ≤ E < 2E_d не может увеличить число атомов каскада (Кинчин и Пиз включают в каскад только те атомы, которые могут создать радиационные повреждения E > E_d)

Отсюда можно записать, что

n(E) = 0, если E < E_d

n(E) = 1, если E_d ≤ E < 2E_d                                      (9.5)

Теперь рассмотрим случай, когда E >> E_d.

Вероятность того, что рассеянный атом будет иметь энергию в интервале (E’,E’+dE) определяется соотношением (9.1).

Исходя из предположения о твёрдых сферах, см. (6.3) и (6.20), имеем:

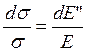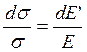 или                                        (9.6)

(в зависимости от того, движение какого атома мы рассматриваем).

Тогда среднее число смешанных атомов, рассеянным атомом равно:

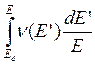 ,                                                  (9.7)

а атом отдачи:

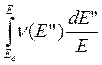.                                                 (9.8)

Сумма этих интегралов должна равняться среднему числу смещений атомов n(E), образованных атомом с энергией E, т.е. мы имеем интегральное уравнение:

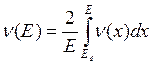                                         (9.9)

Легко проверить, что при  уравнению удовлетворяет функция

n(E) = kE

k – константа, значение которой может быть найдено подстановкой n(2Ed) = 1, 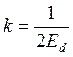      . Откуда

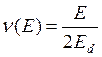   (E >> E_d)                                      (9.10)

(следует напомнить, что в число атомов каскада включаются только те атомы, которые выбиты и их энергия достаточна для создания новых повреждений)

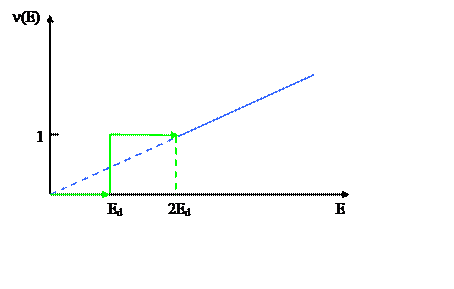
Рис. 9.3. Каскадная функция в модели Кинчина и Пиза.

Снайдер и  Нейфельд предположили, что в каждом соударении теряется энергия E_d

E = E’ + E” + E_d                                                                                   (9.11)

Кроме того, считалось, что атомы после соударения, продолжают двигаться, насколько бы ни была мала их энергия. С одной стороны следовало бы ожидать, что n(E) будет меньше чем у Кинчина и Пиза. Однако благодаря включению в каскад атомов с энергией E < E_d , n(E) должно возрасти. Они получили

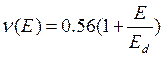,                                           (9.11)

при E > 4E_d вклады компенсируются.

Самое слабое место этих моделей – приближение твёрдых (жёстких) сфер. Однако и с использованием более реалистичных моделей неизменно получается, что n(E) ~ E, все различия определяются лишь значением коэффициента пропорциональности.

Так, для потенциала

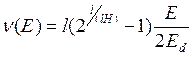
для l = 2

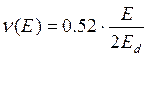
Здесь погрешность состоит в том, что для касательных соударений потенциал  не применим, т.е. не для всех атомов каскада он корректен. По этому к численному значению коэффициентов надо относиться осторожно, но для оценок эти теории полезны.