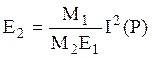Определение дифференциального сечения рассеяния с заданной энергией атома отдачи и полного сечения рассеяния, страница 2

,                                                                                                                                            (6.12)

то есть .

Это характерная черта импульсного приближения. Чем больше Е₁, тем меньше время взаимодействия частиц, и меньше Е₂.

Установим границы применения классического подхода при высоких значениях прицельного параметра. Поскольку должно соблюдаться условие (4.10):

, где 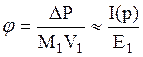     , получаем

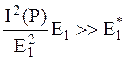
или

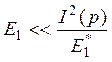.                                                                                                                                            (6.13)

Здесь I(p) – функция только прицельного параметра и потенциала, следовательно, при заданных p и V(r) все определяется значением E₁. В области применимости классического подхода оно должно быть гораздо меньше критического.

Мы получили верхний предел, а не нижний. Это объясняется тем, что при заданных p и V(r) взаимодействие должно протекать достаточно долго, чтобы неопределенностью ΔЕ₂ можно было пренебречь: ΔЕ₂ Δt << ħ.

Типичное значение  для потенциала Борна-Майера в случае пары ион мишень Cu-Cu при p = 1,4 Å равно 10⁷ эВ. Поскольку обычно атомы отдачи при радиационных повреждениях имеют значительно меньшие энергии, а p всегда меньше чем 1,4 Å (= 1/2 D), использование импульсного приближения является оправданным.

Лишь для очень легких элементов, где могут встречаться более слабые потенциалы и более высокие энергии, надо применять квантовую механику.

6.3.Приближение твердых сфер

В столкновениях, близких к лобовым, используют приближение твердых (жестких) сфер.

Пусть при p → 0 и φ → π частицы одновременно останавливаются в точках r₁ = R₁ и r₂ = R₂.

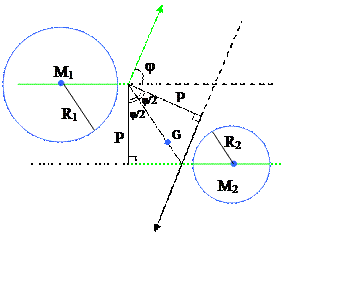
Рис. 6.2.Приближение твердых сфер.

Здесь R₁ + R₂ = ρ₀ минимальное расстояние, на которое способны сблизиться частицы. Потенциальная энергия должна быть при этом равна сумме асимптотических кинетических энергий, т.е.,

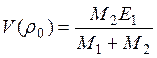.                                                                                                                                            (6.14)

При этом 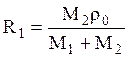               и          .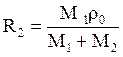

Поскольку мы рассматриваем лобовое или почти лобовое столкновение, можно заменить частицы упругими твердыми сферами с радиусами R₁ и R₂ и массами М₁ и М₂, имеющими те же асимптотические импульсы.

Для частиц, у которых V(r) быстро возрастает в окрестности r = ρ₀, использование твердых (жестких) сфер при относительно невысоких значениях прицельного параметра p является хорошим приближением. Оно работает, естественно, хуже при больших p и малых значениях φ.

Из рис. 6.1 находим, что

p = ρ₀ cosφ/2,                                                                                                                                            (6.15)

тогда

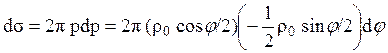,                                                                                                                                            (6.16)

                                                                                                                                            (6.16, а)

Если продифференцировать уравнение (3.19) для асимптотических значений энергий:

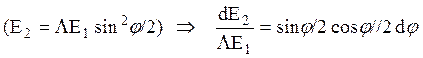,                                                                                                                                            (6.17)

То, с учетом (6.16, a), получаем

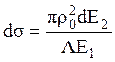.                                                                                                                                            (6.18)

Поскольку полное сечение

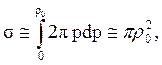                                                                                                                                            (6.19)

то, используя соотношение (6.3):

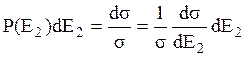, окончательно получаем:

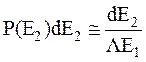                                                                                                                                            (6.20)

Это означает что плотность вероятности в приближении твердых сфер постоянная величина (P(E₂)=1/ΛE₁).

Отсюда следует, что

,

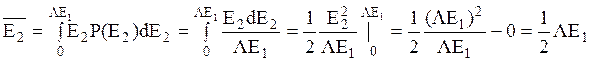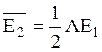.                                                                                                                                            (6.21)