Метод повторных испытаний. Преимущество метода повторных испытаний перед сравнением генеральных средних

§12. Метод повторных испытаний

В медицине очень часто можно использовать метод повторных испытаний, который сопоставим с методом сравнения генеральных средних, но значительно чувствительнее  него. Если раньше, чтобы оценить эффективность лечения,  мы выбирали две группы, одна из которых проходила лечение, а другая нет, то теперь мы набираем одну группу, измеряем у каждого больного значение признака до и после лечения и вычисляем изменение признака.

Преимущество метода повторных испытаний  перед сравнением генеральных средних

Классическая задача математической статистики по установлению различия генеральных средних предполагает использование двух выборок – контрольной  и экспериментальной, которые проходят одно испытание. Метод же повторных испытаний применим в том случае, если возможно проведение эксперимента на одной выборке, которая дважды проходит испытание.

Одной из стандартных медицинских задач, при решении которой можно использовать метод повторных испытаний, является установление того, есть эффект от какого-то препарата или эффекта нет. А в таких опытах обычно важно исключить  психотерапевтическое влияние . Поэтому суть эксперимента состоит в том, что в одном испытании участникам эксперимента дают плацебо, заведомо не оказывающее действия, а в другом – исследуемый препарат. При этом испытуемые в обоих случаях не знают, что они принимают.

В  случае использования одной выборки в эксперименте каждый объект наблюдения дает в каждом из двух испытаний два  значения (пара значений) случайной величины x_i и . При этом x_i – значение СВ для i -го объекта до испытания , –значение этой величины для того же объекта после испытания.

Различие этих значений разность только одного объекта наблюдения обозначим d_i =x_i -. Идея  решения задачи при повторных испытаниях в одной выборке точно та же, что и при сравнении двух выборок.

Нужно сравнить среднее  различие с  ошибкой в нахождении среднего различия. Это сравнение также осуществляется путем вычисления критерия Т  (он называется парный критерий Стьюдента. Распределение Стьюдента используется т.к. генеральная дисперсия неизвестна).

В отличие от предыдущей формулы используется формула:

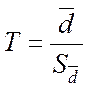, где - среднее значение всех различий, ==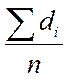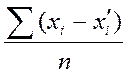,  S - стандартная ошибка в нахождении среднего значения различий  

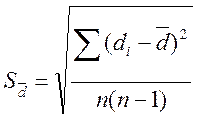
Таким образом выявляется и сопоставляется только изменение признака из-за исследуемого воздействия и его ошибка.

В этом случае чувствительность может быть выше в несколько раз, так как при этом исключается “фоновое” влияние всегда существующего относительно большего объективного разброса значений любого показателя  среди объектов наблюдения.

Итак, алгоритм решения задачи:

1. Выдвинуть  нулевую гипотезу об отсутствии изменений (фактор не влияет) и альтернативную о наличии изменений (фактор влияет).

2. Вычислить величину изменения для каждого объекта d_i=x_i -

3. Вычислить среднее  значение этих изменений  ==  

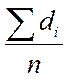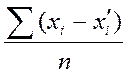
4. Вычислить стандартную ошибку среднего различия  

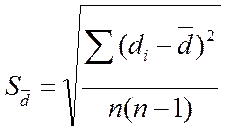
5. Вычислить значение парного критерия Стьюдента

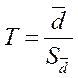
6. Определить критическое значение параметра t для заданного уровня значимости α  для числа степеней свободы k=n-1

7. Сравнить полученное значение Тс t табличным критическим. Если T > t_{табличн}, то отвергаем нулевую гипотезу об отсутствии влияния и принимаем альтернативную гипотезу о влиянии фактора. 

Примечание:

Если обычный критерий Стьюдента требует нормального распределения самих данных, то парный критерий Стьюдента требует нормального распределения их изменений.