Лекция 4. Основные формы математического описания систем управления: уравнения систем
Общие дифференциальные уравнения систем
Общее дифференциальное уравнение системы – это дифференциальное уравнение высокого порядка, которое составляется для выходного сигнала или сигнала ошибки.
Правила записи таких уравнений совпадают с правилами записи уравнений динамических звеньев за исключением требования единичного значения коэффициента при выходном сигнале.
Если получены передаточные функции замкнутой линейной системы, переход к общему уравнению выполняется на основе принципа суперпозиции.
Для выходного сигнала:
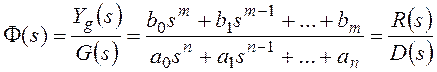 ,
,
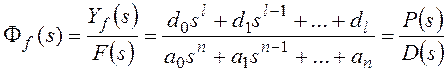 ,
,
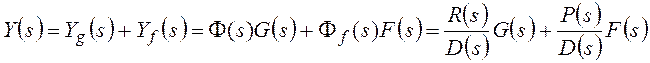 ,
,
![]() ,
,
![]() ,
,
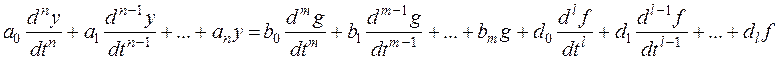 .
.
Для сигнала ошибки:
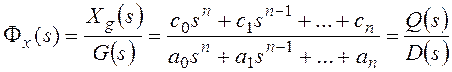 ,
,
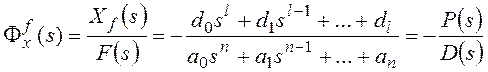 ,
,
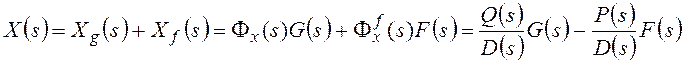 ,
,
![]() ,
,
![]() ,
,
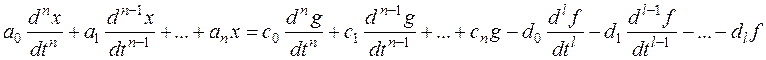 .
.
Для нелинейной системы, когда невозможно получение использованных выше передаточных функций, общие дифференциальные уравнения получают на основе совокупности уравнений динамических звеньев системы путем исключения промежуточных переменных.
Системы дифференциальных уравнений
Эта форма математического описания имеет наиболее важное значение для нелинейных систем, но все более широко используется и для линейных систем, прежде всего при автоматизированном расчете процессов в системах высокого порядка.
Модель представляет собой систему дифференциальных уравнений первого порядка (форма Коши). Ее составление основано на понятии фазового пространства системы.
Фазовое пространство, или пространство состояний системы, это n-мерное пространство, координатами в котором являются фазовые переменные (переменные состояния) системы. Размерность фазового пространства соответствует размерности системы, то есть порядку системы дифференциальных уравнений в нормальной форме (форме Коши), описывающих данную систему.
В общем случае для нелинейной системы такая модель имеет вид:
 i=1,2,...,n, где
ji – нелинейные функции; xi
– фазовые переменные системы (базис); g, f– задающее
и возмущающее воздействия (возможно, векторные функции).
i=1,2,...,n, где
ji – нелинейные функции; xi
– фазовые переменные системы (базис); g, f– задающее
и возмущающее воздействия (возможно, векторные функции).
Для линейной системы модель принимает вид:
 , i=1,2,...,n, где
uj, j=1,2,…r
– входные сигналы системы (задающие и
возмущающие воздействия); ail, bij–
коэффициенты уравнений, для
нестационарной системы все или часть коэффициентов зависят от времени.
, i=1,2,...,n, где
uj, j=1,2,…r
– входные сигналы системы (задающие и
возмущающие воздействия); ail, bij–
коэффициенты уравнений, для
нестационарной системы все или часть коэффициентов зависят от времени.
Необходимо отметить, что при выборе базиса отсутствует требование совпадения переменных состояния с входными и выходными сигналами звеньев системы. Базис стараются выбирать из соображений удобства получаемой модели для последующей работы.
Рассмотрим порядок получения моделей в форме общих уравнений и системы дифференциальных уравнений на примере следящей системы.
Набор передаточных функций замкнутой системы выглядит следующим образом:
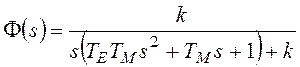 ,
,
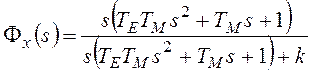 ,
,
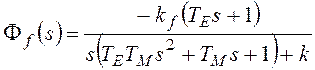 ,
,
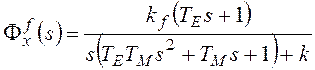 .
.
Выделим полиномы в числителях и знаменателях передаточных функций:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Составим общие дифференциальные уравнения системы:
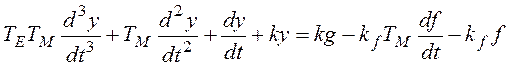 ,
,
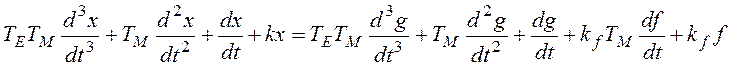 .
.
Теперь на основе уравнения для выходного сигнала составим систему уравнений первого порядка:
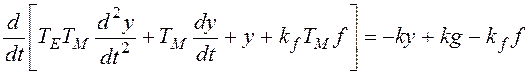 ,
,
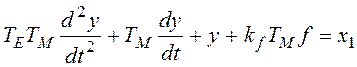 ,
,
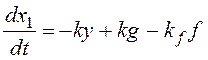 ,
,
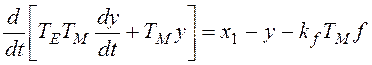 ,
,
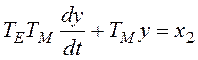 ,
,
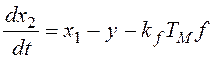 ,
,
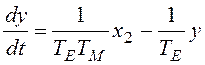 .
.
Введем обозначения
x3=y, u1=g, u2=f
и запишем полученную систему уравнений:
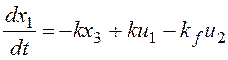 ,
,
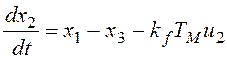 ,
,
 .
.
Обычно такую модель дополняют уравнением выхода, дающим связь выходного сигнала с фазовыми переменными: y=x3.
Векторно-матричная форма модели системы
Эта форма используется для линейных систем. Она тесно связана с моделью в виде системы дифференциальных уравнений и по существу является компактной формой записи последней. В общем случае векторно-матричная форма представляет собой следующую совокупность уравнений:
![]() ,
,
![]() , где X=(x1,x2,…xn) – вектор
фазовых переменных, U=(u1,u2,…ur) – вектор
входных сигналов, Y=(y1,y2,…yl) – вектор
выходных сигналов, A – квадратная
матрица размерностью
, где X=(x1,x2,…xn) – вектор
фазовых переменных, U=(u1,u2,…ur) – вектор
входных сигналов, Y=(y1,y2,…yl) – вектор
выходных сигналов, A – квадратная
матрица размерностью ![]() , B – матрица входов размерностью
, B – матрица входов размерностью
![]() , C– матрица выходов
размерностью
, C– матрица выходов
размерностью ![]() .
.
Первое уравнение называют уравнением состояний, второе – уравнением выходов.
Для примера модели следящей системы имеем: n=3, r=2, l=1;
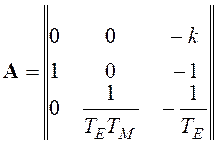 ,
,
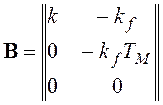 ,
,
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.