Частотный критерий устойчивости Найквиста, страница 2

Рассмотрим два следующих примера.

Для передаточной функции разомкнутой системы

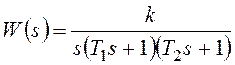
АЧХ и ФЧХ описываются выражениями:

,  .

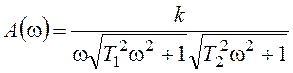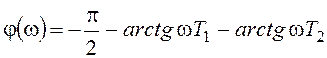АФХ системы показана на рисунке 100а.

Для передаточной функции разомкнутой системы

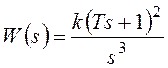
АЧХ и ФЧХ описываются выражениями:

,  .

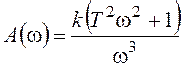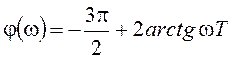АФХ системы показана на рисунке 100б.

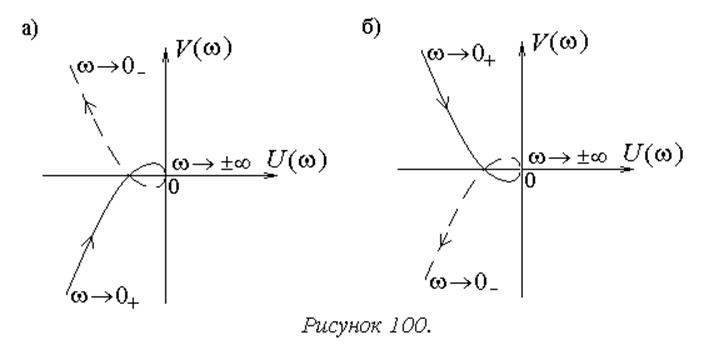
В обоих случаях применить критерий не удается, так как АФХ претерпевают разрыв на частоте, соответствующей нулевым корням полиномов Q, то есть при w=0.

Рассмотрим первую из этих систем как предельный случай рассмотренной выше системы (рисунок 98), представив передаточную функцию в форме

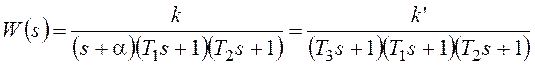, где , , .

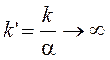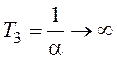Обратимся к малому диапазону частот в окрестности нуля -w’<w< w’, где 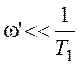, 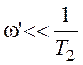. Для этого диапазона получим:

,

,

.

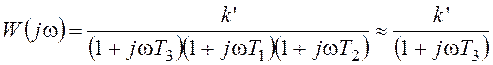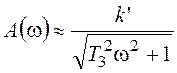С учетом величины k’ и T₃ отметим, что при изменении частоты от -w’ до w’ значение ФЧХ изменится от  до  при сохранении бесконечно больших значений ФЧХ. Следовательно, для АФХ на рисунке 98 участок, лежащий в первом и четвертом квадрантах, деформируется в дугу бесконечно большого радиуса длиной p, движение по которой при увеличении частоты происходит по часовой стрелке.

Если теперь вернуться к исходному виду АФХ (рисунок 100а) и полному диапазону частот от - до , можно дополнить ее дугой бесконечно большого радиуса длиной p в направлении по часовой стрелке. Благодаря этому АФХ становится замкнутой кривой, что позволяет однозначно применить критерий устойчивости Найквиста (рисунок 101).

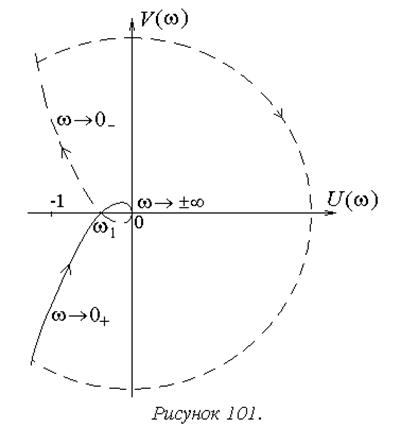
В соответствии с рисунком 101 с учетом l=0 для устойчивости замкнутой системы должно иметь место  или . Найдем w₁:

,

,

,

:   .

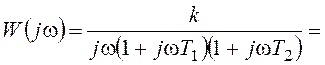
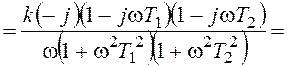
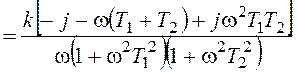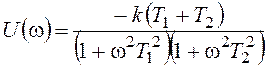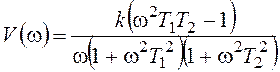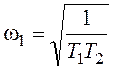Получим условие устойчивости:

, 

.

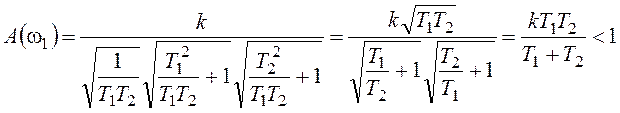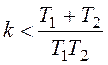Аналогичные рассуждения для общего случая с кратными нулевыми корнями знаменателя передаточной функции разомкнутой системы

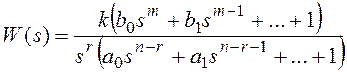
дают увеличение длины дополняющей дуги в r раз, где r – кратность корня.

Для рассмотренного выше примера с r=3 АФХ, представленную на рисунке 100б, потребуется дополнить дугой длиной 3p, в результате чего ее анализ становится весьма трудоемким.

В таких случаях допустимо применение приема, использованного выше для систем, устойчивых в разомкнутом состоянии, – ограничиться половиной АФХ – для положительных частот, дополнив положительной вещественной полуосью и дугой бесконечно большого радиуса длиной .

Построение для рассматриваемого примера выполнено на рисунке 102.

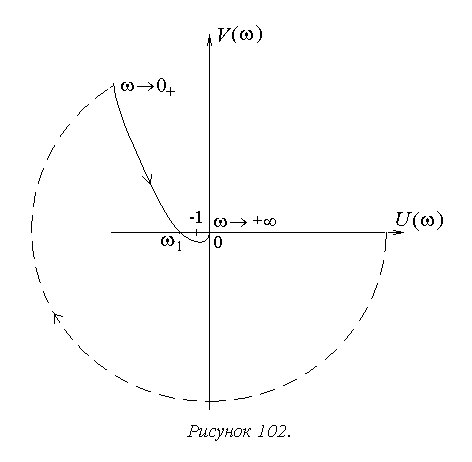
Из рисунка видно, что условие устойчивости данной системы может быть получено на основе неравенства или . Воспользуемся первым из них.

Найдем частоту w₁:

,

,

,

,   .

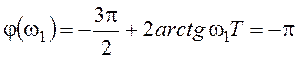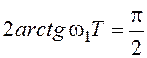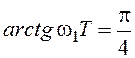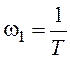Получим условие устойчивости:

,

,

.

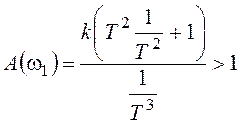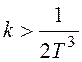Теперь рассмотрим пример системы, находящейся в разомкнутом состоянии на колебательной границе устойчивости:

.

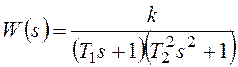АЧХ и ФЧХ описываются выражениями:

,  .

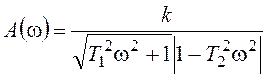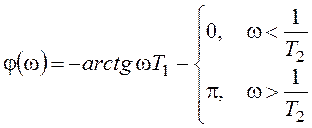АФХ системы для  показана на рисунке 103.

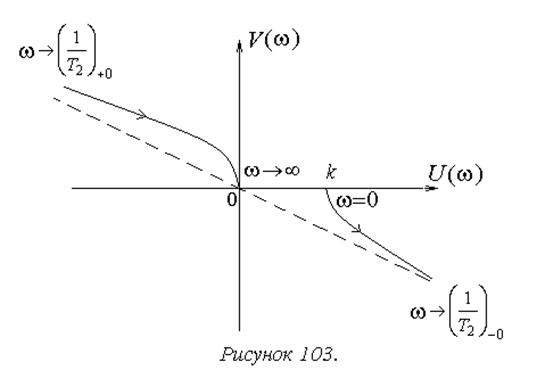
Прямо применить критерий, как и выше, не удается, так как АФХ претерпевают разрыв на частоте 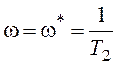, соответствующей мнимым корням полинома Q. В окрестности этой частоты , ФЧХ изменяется скачкообразно на величину .

Воспользуемся тем же, что и ранее, приемом и представим рассматриваемую передаточную функцию в следующей форме

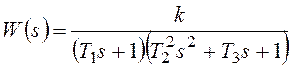
где .

Теперь выражения для АЧХ и ФЧХ примут вид:

,

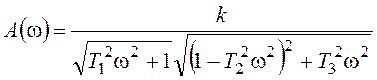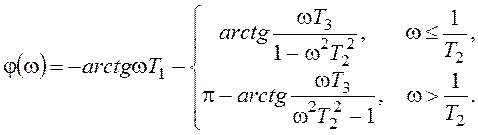
С учетом величины T₃ и известных свойств колебательного звена отметим, что величина резонансного пика в окрестности частоты 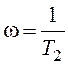 будет стремиться к бесконечности и в той же малой окрестности произойдет изменение значений ФЧХ на величину, стремящуюся к .

В результате приходим к тому же правилу дополнения АФХ дугой бесконечно большого радиуса длиной p в отрицательном направлении (по часовой стрелке) на частоте, соответствующей мнимому корню знаменателя передаточной функции разомкнутой системы.

Дополненная таким образом АФХ для рассматриваемого примера представлена на рисунке 104, который позволяет сделать вывод о неустойчивости этой системы независимо от значений ее параметров.

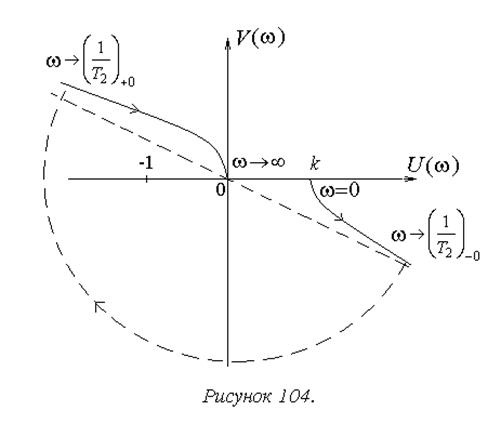
Итак, при наличии в знаменателе передаточной функции разомкнутой системы нулевых и чисто мнимых корней для использования критерия Найквиста АФХ разомкнутой системы дополняется дугами бесконечно большого радиуса в направлении по часовой стрелке на всех частотах, соответствующих таким корням. Длина каждой дуги rp, где r – кратность корня.

При использовании для анализа устойчивости ветви АФХ, соответствующей положительным частотам, она дополняется в окрестности w=0 положительной вещественной полуосью и дугой бесконечно большого радиуса длиной .

Отметим еще одну форму критерия Найквиста, эквивалентную рассмотренной. Она основана на подсчете переходов АФХ через отрезок вещественной оси, лежащий левее точки (-1; 0j). «Положительным» называют переход в направлении против часовой стрелки, соответствующем положительному направлению отсчета углов, «отрицательным» - переход в противоположном направлении. Если АФХ или рассматриваемая ее часть начинается на указанном участке, имеет место «полупереход» с соответствующим направлению АФХ знаком.

В таких терминах критерий сводится к соблюдению равенства:

, если рассматривается полная АФХ, или для ветви АФХ, соответствующей положительным частотам

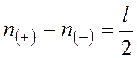, где n₍₊₎ – количество «положительных» переходов, n_(-) – количество «отрицательных» переходов, l - количество корней знаменателя передаточной функции разомкнутой системы, лежащих в правой полуплоскости.

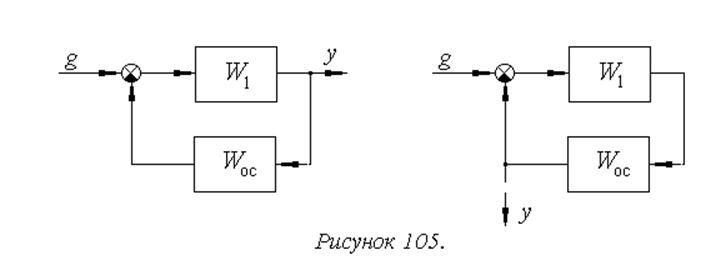
Обобщение критерия Найквиста на системы с произвольной обратной связью

Устойчивость – это собственное свойство системы, не зависящее от наличия и точек приложения входных сигналов, а также от точки наблюдения процесса в системе. Поэтому для системы с произвольной обратной связью (рисунок 105а) можно формально перенести точку, в которой наблюдается выходной сигнал (рисунок 105б), и получить следующий вывод: при использовании критерия Найквиста для системы с произвольной обратной связью следует рассматривать годограф произведения передаточных функций прямой цепи и обратной связи .