Обобщенная схема ЦОС. Дискретизация аналогового сигнала. Основная полоса частот. Описание линейных дискретных систем в частотной области. Понятие частотной характеристики (ЧХ). Связь ЧХ с передаточной функцией. Алгоритм быстрого преобразования Фурье с прореживанием по времени. Понятие о полиномах Чебышева, страница 4

11.1.2  Понятие о полиномах Чебышева.

Результатом решения сформулированной ранее задачи аппроксимации в частотной области является некоторый тригонометрический полином порядка М=M_opt вида (11.1). Задача сводится к поиску коэффициентов полинома. Такая аппроксимация называется полиномиальной. Тригонометрический полином (11.1) 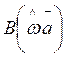 можно выразить в более удобной форме, если использовать замену переменной

откуда

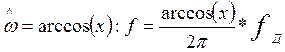
При такой замене переменной аппроксимирующий полином

представляется в виде

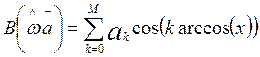, (11.4)

Стоящая под знаком суммы функция

, (11.5)

также является полиномом K-го порядка, получившим название полинома Чебышева.

Полином Чебышева N-го порядка имеет вид

, (11.6)

Убедимся, что (11.6) действительно представляет собой полином по x(-1≤x≤1) степени N с вещественными коэффициентами

N=0
N=1
N=2

Зная полином 1-го и 2-го порядков, получим рекуррентную формулу для представления полиномов степени N≥3.

В целях удобства обозначим:

Q=arcos(x)

Тогда из (11.6) следует:

Суммируя эти два равенства получаем

, (11.7)

Учитывая соотношения

cos(NQ)=C_N(x) и cos(Q)-cos(arcos(x))=x

Из (11.7) окончательно получаем рекуррентную формулу для конструирования полиномов Чебышева.

, (11.8)

на основании которой нетрудно получить следующий ряд полиномов.

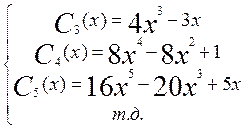, (11.9)

Непосредственно из определения полинома Чебышева, а также из формул (11.8) и (11.9) следует:

1.  коэффициент полинома С_N(x) при старшей степени x равен 2^N-1

2.  для всех x и любого N выполняется неравенство .

В теории ортогональных функций доказывается, что из всех полиномов степени N с коэффициентом при старшем члене 2^N-1 полином Чебышева C_N(x) наименее уклоняется от нуля, что и требуется по условию задачи. Таким образом, аппроксимирующий тригонометрический полином 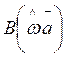 может быть представлен в виде суммы полиномов Чебышева с ……

и поставленная ………………………………

                     

В данном примере аппроксимирующий полином имеет вид

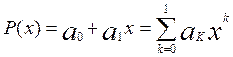
поэтому в соответствии с вышеупомянутой теоремой Чебышева число точек альтернанса знакочередующихся экстремальных точек должно быть не менее чем m=M+2=1+2=3.

Шаг 1. Выбор начального приближения.

В качестве начального приближения выберем в области  произвольную сетку.

Шаг 2. Решение системы из трех линейных уравнений вида (17.1) на сетке S⁽⁰⁾  i=0,1,2, где (-1)ⁱ обеспечивает колебательный характер поведения ошибки P(x).

Решением этой системы являются: a₀=-0,3125; a₁=1,25; b₀=0,0625.

Шаг 3. вычисление ошибки  на густой сетке  (например, через шаг 0,0001)

с тем, чтобы определить, существуют ли знакочередующиеся экстремальные точки, где ошибки . Оказывается, что таких точек 3: при х=0 ; в точке х=0,625  и в точке х=1 . Таким образом, нулевое приближение не дало желаемого результата, поэтому необходимо назначить новую сетку и перейти к шагу 2.

Повторяемый шаг 2. Составим новую пробную сетку

, для которой систему уравнений (запишем в матричном виде)

Решением этой системы являются: a₀=0,1328125; a₁=1; b₁=0,1171875. Необходимо проверить полученное решение на оптимальность, для чего требуется повторить шаг 3.

Повторяемый шаг 3. Вычисление ошибки  на густой сетке .

с тем чтобы определить знакочередующиеся экстремальные точки, где . Таких точек три: в двух из них х=0 и х=1 ошибка равна b₁=0,1171875≈0,117, а третья ошибка в точке х=0,5 максимальна по абсолютной величине и равна . Видно, что и новое приближение не дало желаемого результата, поэтому необходимо назначить очередную сетку и повторить итерацию, начиная с шага 2.

Повторяемый шаг 2. назначаем новую сетку

для которой система уравнений в матричной форме имеет вид

Решением этой системы являются: a₀=-0,125; a₁=1; b₂=0,125 и максимум ошибки  (см. …)

Вследствие равенства  ошибок на заданной сетке и чередования их знаков в соответствии с теоремой Чебышева можно утверждать, что полученное решение является оптимальным и аппроксимирующий полином имеет вид

(Рисунок 17)