Основы теории делимости. Основная теорема теории чисел. Алгоритм Евклида и цепные дроби. Разложение числа в цепную дробь, страница 12

f^*(x)=A₀x^s+A₁x^s+1+…+A_nx^s+n

Пример: f(x+2)=f(x+1)+f(x)  (xÎZ!!!)

f_n+2=f_n+1+f_n

f₀=f₁=1

x²-x-1=0  - характеристическое уравнение l₁=(1+Ö5)/2; l₂=(1-Ö5)/2

f_n=C₁l₁ⁿ+C₂l₂ⁿ=C₁((1+Ö5)/2)ⁿ+C₂((1-Ö5)/2)ⁿ – общее решение

   С₁+С₂=0                           С₁=1/Ö5

С₁+С₂=Ö5(С₁-С₂)=2        С₂=-1/Ö5

; 

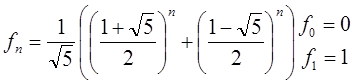
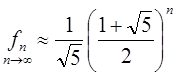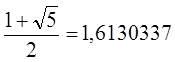
|110…0|

|111…0|

f_n=     |0111..0|

|0..1110|

|0…111|

|0…011|

l²-l+1=0   |   l₁=e^i(p/3)   ; l₂=e^-i(p/3)

C₁Cos(p/3)x+C₂Sin(p/3)x       C₁=1

C₁Cos(p/3)+C₂Sin(p/3)=1       C₂=1/Ö3

f_n=Cos(p/3)n+(1/Ö3)Sin(p/3)n

f(x+2)-5f(x+1)+6f(x)=x²-2x+1

l²-5l+6=0    l₁=2

l₂=3

C₁2^x+C₂3^x

f^*(x)=A₀+A₁x+A₂x²

A₀+A₁(x+2)+A₂(x+2)²-5(A₀+A₁(x+2)+A₂(x+2)²)+6(A₀+A₁x+A₂x²)=x²-2x+1

A₀=1/2; A₁=-1/6;  A₂=½

½-1/6x+½x²+C₁2^x+C₂3^x – общее решение неоднородного уравнения

Основы теории графов

1)  G=(V,E)

V={a₁,a₂,…,a_k}

E={(a,b)|aÎV, bÎV} – множество неупорядоченных пар

(a,b)=(b,a)    a –––––– b

(a,a) – называется петлей

Если 2 вершины графа соединены не более, чем 1 ребром, то граф называется линейным.

V=(a,b)ÎE

a,b называется концевыми точками ребра V, ребро V инцидентно вершинам a,b, вершины a,b называются смежными.

d(a)={V=(a₁,a₂)ÎE}  :  a₁=a  или  a₂=a  }  называется звездой

|d(a)| - deg a  число ребер в звезде = степени вершины.

Теорема: 39

|E|= ½ S_aÎV deg a

Следствие:

Для любого графа число вершин нечетной степени четно.

Вершина a называется изолированной, если deg (a)=0

a

 

Вершина a называется висячей (концевой) если deg(a)=1

Пусть существует G(V,E)

V`ÍV, E`ÍЕ

G`=(V`,E`)- подграф графа G

Граф является подграфом самого себя.

Пустой граф – подграф

Остальные графы являются собственными

Определение: Путь

a₀x₁a₁x₂…a_L-1x_La_L – a_iÎV,   x_i=(a_i-1;a_i)ÎE

- пусть длины L (т.е. длиня любого ребра = L)

a₁                          a₃

a_{2                          …}           a_L

Если a₀ ¹a_L (начальная вершина и конечная вершина не совпадают.), то путь называется открытым или незамкнутым, иначе путь называется циклическим, или замкнутым.

Если в пути все ребра различны x_i¹x_j (i¹j) (вершины могут совпадать), путь называется простым.

Открытый путь, где все вершины различны. a_i¹a_j (i¹j) называется цепью.

Замкнутый простой путь, где все вершины различны называется циклом.

Как ходить по графу?

1 метод. Depth first search – поиск в глубину.

Применим стек filo.

V₀ – конечная вершина. В стек если есть непомеченные смежные вершины

??????

Как только вершина из которой ???

Пример:

????

2 метод. Breadth first search – поиск в ширину

Очередь (магазин)  fifo

Просматриваем вершину à очередь

Записываем в очередь все смежные с ним вершины просмотренные

Пример:

????

Теорема: 40

Если существует путь из a-b то из ребер этого пути можно построить цепь.

a=a₀x₁a₁x₂a₂…x_La_L=b

x_i=(a_i-1, a_i)

Рассмотрим множество всех лучей из a₀b в которые можно построить из ребер: {x₁, x₂,…,x_L} Это множество ¹Æ

Рассмотрим самый короткий путь.

a=a`<sub>0</sub>x`₁a`<sub>1</sub>x`₂a`<sub>2</sub>…x`_La`_L=b

Утверждение: a`<sub>i</sub>¹a`_j Если это не так, то этот кусок можно было выкинуть, и путь стал был короче. Значит наше предположение не верно. Вершины не повторяются.

Теорема: 41

Если существует замкнутый простой путь, то из его ребер можно было построить цикл.

Доказательство:

a=a₀x₁a₁x₂a₂…x_La_L=b   -  ребра не совпадают

Пусть вершины совпадают.

{x₁…x_L} – построим путь из этих ребер, если вершины совпадают их можно выкинуть => путь короче.

Теорема: 42

Пусть существует G=(V,E), все вершины имеют четную степень, тогда для любые ребра найдется замкнутый простой путь, содержит это ребро.

Доказательство:

x₁=(a₀,a₁)           x₁  a₁   x₂

a₀                a₂

В силу четности можно…

Теорема: 43

Все вершины имеют четную степень

G=(V,E),  E¹Æ

То множество ребер можно представить как объединение не пересекающихся циклов.

Доказательство:

x₁ÎE строим замкнутый простой путь для ребра (по теореме 42)

вершины могут повторяться.

a=a₀x₁a₁x₂a₂…x_ka_k  Пусть a_k=a₀

Как только вершины повторяются – цикл.

Его можно удалить из графа, по вершине по прежнему – четный.

(V, E\{цикл})  и т.д.

Получим объединение циклов