Этап построения математической модели (этап 2, рис. 1.2) является наиболее важным этапом в математическом моделировании. Представления о механизмах и законах, которые действуют в системе и которые закладываются в математическую модель, определяют рамки результатов моделирования. Так, при моделировании функционирования сердечно-сосудистой системы на основе представлений о работе сердца с позиций механики можем построить механико-математическую модель.
Когда речь идет о математическом моделировании динамики сложной биологической системы, основанном на физических законах, мы вторгаемся в область математической биофизики сложных систем. Именно на стыке трех наук: математики, физики и биологии в последние пять десятилетий произошел качественный скачок в математическом описании поведения любой системы (физической, биологической, экономической).
Обычно принято измерять физиологические величины как функции времени. Для характеристики таких временных зависимостей существуют четыре основных математических понятия: стационарные состояния, колебания, хаос и шум. Стационарное состояние в математике может быть связано с понятием гомеостаза в физиологии, например, среднее артериальное давление поддерживается постоянным у человека. При физической нагрузке давление повышается, а после прекращения физической нагрузки давление в течение нескольких минут возвращается до стационарного уровня. Примерами колебательных процессов в организме человека могут служить: ритмы сердцебиения, дыхания и размножения клеток, циклы сна и бодрствования, секреции инсулина, перистальтические волны в кишечнике и мочеточнике, электрическая активность коры головного мозга и автономной нервной системы и т. п. Известно, что даже тщательное измерение физической или физиологической величины никогда не дает абсолютно стационарной или строго периодической временной зависимости. Всегда будут наблюдаться флуктуации (отклонения) вокруг некоторого фиксированного уровня или периода колебаний. Кроме того, существуют системы настолько нерегулярные, что трудно найти лежащий в их основе стационарный или периодический процесс. Такие процессы рассматриваются в математике либо как шум (относящийся к флуктуациям), либо как хаос («наивысшая степень» порядка, нерегулярность, наблюдаемая в детерминированной системе). Хаос может наблюдаться и при полном отсутствии шума в окружающей среде.
Основу математической модели составляет система математических уравнений (формула 1.1). Динамическая математическая модель характеризует поведение системы во времени, которое можно описать с помощью таких физических понятий, как скорость и ускорение. Динамические модели описываются системами дифференциальных уравнений, на которые накладываются ограничения, вытекающие из физического или физиологического смыслов принятых величин:
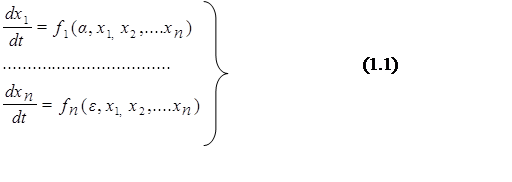
где f1,…, fn - некоторые функции, x1,…, хп – независимые переменные, п - размерность фазового пространства, a,…, e и т. д. - параметры дифференциальных уравнений.
Стационарные устойчивые состояния соответствуют постоянным решениям уравнений системы 1.1 (рис. 1. 3, А). Стационарным колебаниям биологических или физических величин соответствуют периодические решения системы уравнений (рис. 1.3, Б). Нерегулярные (апериодические) временные решения уравнений соответствуют шуму или хаосу (рис 1.3, В).
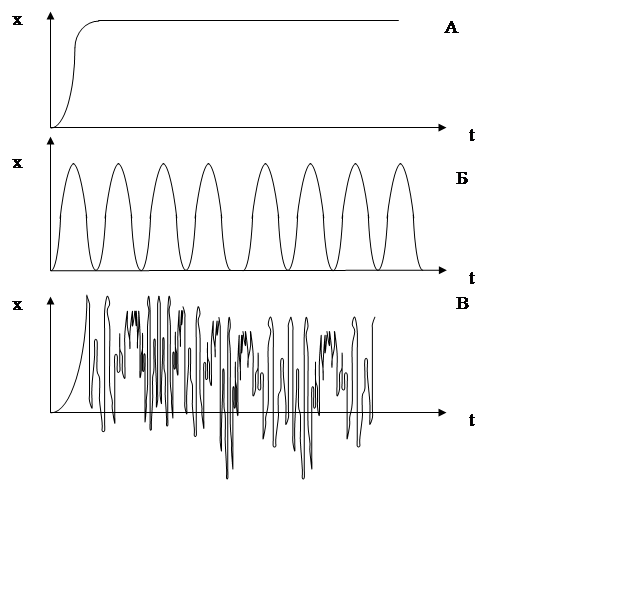 |
Рис. 1.3. Типы решений дифференциальных уравнений.
При некоторых значениях параметров возможно получение нескольких решений, то есть система может находиться в нескольких стационарных состояниях (например, в двух состояниях). Переход системы, в результате которого она может оказаться в одном из возможных состояний, называется бифуркацией. Обычно одни состояния являются устойчивыми, другие – неустойчивыми. Если возможны два устойчивых состояния, то система может перескакивать из одного состояния в другое при незначительном внешнем воздействии, в том числе при флуктуации. Это явление называется бистабильностью.
В качестве примера построения модели периодического биологического процесса рассмотрим математическую модель «хищник - жертва» Вольтерра.
Модель Вольтера
Пусть в некотором замкнутом районе живут зайцы и рыси. Зайцы питаются растительной пищей, имеющейся всегда в достаточном количестве. Рыси (хищники) питаются только зайцами (жертвами). Обозначим число зайцев в этом районе через N1, а число рысей через N2. N1 и N2 являются функциями времени.
Так как количество пищи для зайцев не ограничено, мы можем считать, что при отсутствии хищников, их число возрастало бы с течением времени t прямо пропорционально числу имеющихся особей:
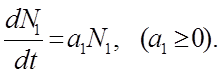
где ai – коэффициент пропорциональности.
Если бы в данном районе жили только рыси, то они бы вымерли из-за отсутствия пищи:
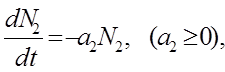
т. е. скорость вымирания пропорциональна числу особей.
Рассмотрим ситуацию, когда в данном районе живут и рыси , и зайцы. Тогда количество зайцев будет уменьшаться пропорционально числу встреч рыси и зайца (b1N1N2):
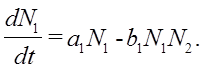
Количество рысей будет возрастать пропорционально числу встреч рыси и зайца:
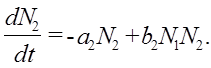
Тогда поведение системы «хищник-жертва» будет описываться системой из двух дифференциальных уравнений:
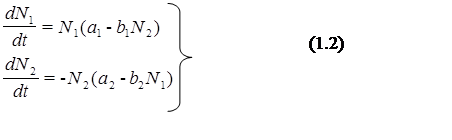 |
где a1, a2, b1, b2 – некоторые коэффициенты пропорциональности, определяемые по опытным данным.
На рис. 1.4. приведены графики функций численности рысей и зайцев от времени. Видно, что эти функции являются периодическими функциями времени, и максимум численности зайцев всегда опережает максимум численности рысей.
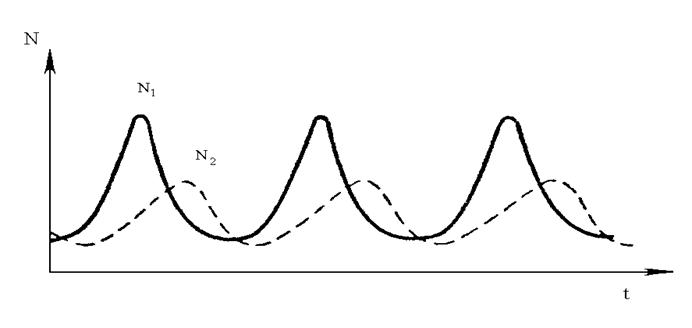
Рис. 1.4. Зависимость численности рысей и зайцев от времени.
Посмотрим, что происходит на практике. На рис. 1.5 приведен пример реальных колебаний численности северо-американского зайца и рыси в Канаде.
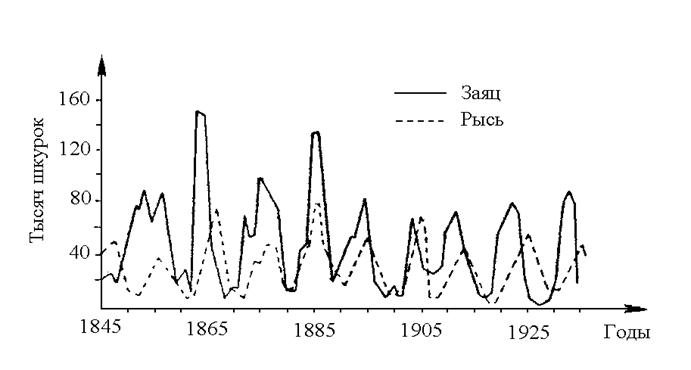
Рис. 1.5. Колебания числа сданных охотниками шкурок рысей и зайцев в Канаде в 1845-1950 гг.
Видно, что периоды колебаний численности зайцев и рысей примерно одинаковы (9-10 лет). При этом максимум численности зайцев опережает максимум численности рыси на 1 год. Экспериментальные кривые не имеют столь правильную форму, как кривые, полученные на основе математической модели. На практике нужно учитывать не только взаимоотношения основных партнеров (зайцев и рысей), но и наличие других хищников и жертв, различные климатические условия и т. д.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.