Указания к решению задач контрольных работ № 1-5 по курсу "Математика" (Использовать свойства степени с действительным показателем. Использовать область определения неравенства и знаки дроби), страница 2

B7. Найти область определения уравнения, решить уравнение и выбрать значения х из этой области.

B8. Выделить полный квадрат, применить формулу синуса двойного угла, решить полученное уравнение и сделать отбор корней из заданного отрезка.

B9. Использовать формулу 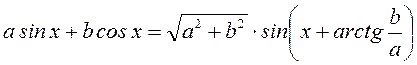, найти область изменения полученной функции.

B10. Разность косинусов преобразовать в произведение, применить формулу синуса двойного угла, решить уравнение и сделать отбор корней, принадлежащих заданному интервалу.

B11. Использовать область определения арккосинуса и существование дроби.

B12. Использовать область определения функции арксинуса и ее монотонность.

B13. Разность синусов преобразовать в произведение, разложить на множители, решить уравнения и сделать отбор корней.

B14. Применить формулу синуса двойного угла.

B15. Сделать замену переменной и решить дробно – рациональное неравенство.

B16. Использовать формулы приведения и формулу тангенса двойного угла.

B17. Убрать период функции синуса, использовать формулы приведения, найти котангенс, тангенс и косинус полученного аргумента.

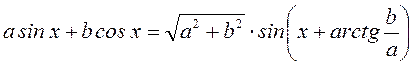B18. Преобразовать функцию к виду , использовать формулу , найти область изменения полученной функции.

B19. Применить формулу тангенса суммы двух углов.

B20. Найти область определения уравнения, использовать формулы приведения, решить уравнение и сделать отбор корней.

B21. Опустить период функции синуса, использовать формулы приведения.

B22. Функцию синуса заменить на косинус дополнительного аргумента.

B23. Найти период каждого слагаемого и период данной функции найти как наименьшее общее кратное периодов слагаемых.

B24. Решить неравенство с помощью тригонометрического круга.

B25. Взять тангенс левой и правой части уравнения.

Часть III

C1. В правой части уравнения оставить только а, найти область изменения функции, оказавшейся в левой части уравнения.

C2. Уравнение свести к квадратному и взять .

C3. Заданный промежуток принадлежит первой четверти тригонометрического круга, причем,  принадлежит этому промежутку, в этой точке функция имеет наибольшее значение. Использовать монотонность заданной функции и найти значение функции на концах отрезка.

C4. Записать площадь треугольника через переменную x, найти производную этой функции и исследовать ее на наибольшее значение.

C5. Выяснить, сколько корней может иметь каждое из этих уравнений и решить второе уравнение при найденном значении а.

Контрольная работа №3

Часть I

А1. Использовать теорему о неравенстве треугольника.

А2. Векторы , D – искомая точка.

А3. Использовать формулу для вычисления длины вектора.

А4. Катет, лежащий против угла в 30^о, равен половине гипотенузы.

А5. Следствие из теоремы косинусов.

А6. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.

А7. Использовать формулу для вычисления координат середины отрезка.

А8. Координаты коллинеарных векторов пропорциональны.

А9. Использовать свойство биссектрис треугольника.

А10. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.

Часть II

В1. Площадь параллелограмма равна произведению его смежных сторон, на синус угла между ними. Зная скалярное произведение, можно найти произведение сторон.

В2. Записать координаты точки D в общем виде, Q – середина BD, вычислить координаты середины отрезка и затем вектора .

В3. Векторы перпендикулярны, значит их скалярное произведение равно нулю.

В4. Векторы коллинеарны, значит, их координаты пропорциональны.

В5. Точка D – середина АС. Использовать формулу для нахождения косинуса угла между векторами.

В6. Угол будет прямым, если скалярное произведение векторов, образующих его, равно нулю. Проверить все углы треугольника.

В7. Найти координаты соответствующих векторов, затем вычислить их длины.

В8. Достроить треугольник до параллелограмма, так, чтобы медиана оказалась половиной диагонали. Параллелограмм делится диагональю на равновеликие треугольники. Использовать формулу Герона.