Математика \ Математика

Математический анализ функции одной переменной: Учебное пособие. Часть 2 (Производные высших порядков. Ряд Тейлора. Раскрытие неопределенностей. Сходимость ряда Тейлора. Ряд Лорана), страница 4

Действительно, согласно признаку Коши, знакопостоянный ряд сходится если ,что эквивалентно условию . Вторая из формул (96) доказывается аналогично на основе признака Даламбера.

Теорема 2: Сумма степенного ряда есть функция непрерывная и бесконечно дифференцируемая внутри круга сходимости. Пишут .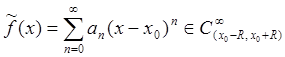

Теорема 3 (Абеля): Если степенной ряд сходится в какой – либо точке на границе круга сходимости, то имеет место непрерывность изнутри круга сходимости.

Пример 2: Определить область сходимости рядов Тейлора (94 a-c).

Для имеем: 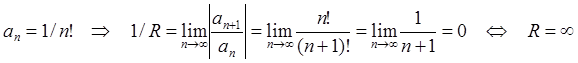, то есть ряд сходится при любых (внутри круга с бесконечным радиусом).

Для разложение ведется не по степеням , а по степеням , получаем: .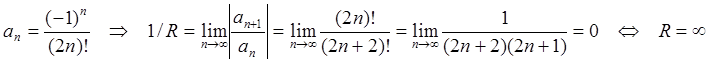

Аналогичный результат справедлив и для . Пишут .

Определение 3: Аналогами точек разрыва функции вещественной переменной для функции комплексной переменной являются особые точки на комплексной плоскости – точки, в окрестности которых функция не может быть разложена в ряд Тейлора.

Теорема 4: Радиус сходимости ряда Тейлора равен расстоянию от точки разложения до ближайшей к ней особой точки .

Действительно, согласно Т2, внутри круга сходимости функция не может иметь особых точек. Можно показать, что расходимость на границе круга обусловлена появлением особой точки.

Пример 3: Исследовать сходимость ряда Тейлора для функции в окрестности точки .

Ряд Тейлора имеет вид: 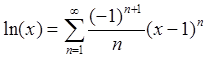(смотри (94d)). Единственной особой точкой для функции является точка ветвления . Согласно Т4: . Радиус сходимости может быть вычислен и по формулам (96). Действительно, .

Согласно теореме Абеля, на границе интервала сходимости имеем:

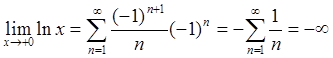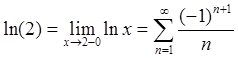при : (смотри параграф 10, пример 3); при : (смотри параграф 15, пример 5).

Таким образом, точный интервал сходимости имеет вид .

Пример 4: Исследовать сходимость ряда Тейлора для функции в окрестности точки .

Ряд Тейлора имеет вид: 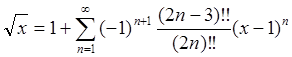(смотри (94e)). Единственной особой точкой для функции является точка ветвления . Согласно Т4: . Использование формул (96) приводит к такому же результату: .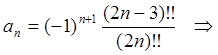

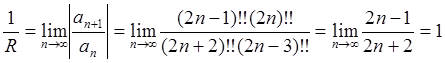При имеем: 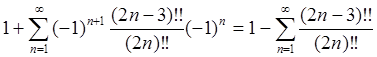. Исследуем сходимость ряда 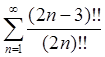. Поскольку 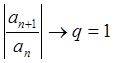, признак Даламбера оказывается недостаточным, более общий признак Раабе дает (смотри параграф 10): 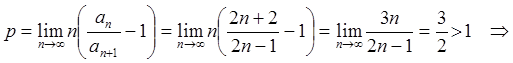ряд сходится. Согласно теореме Абеля, в случае сходимости на границе интервала сумма ряда равна пределу функции изнутри интервала сходимости: 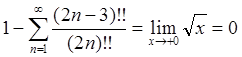, откуда заключаем

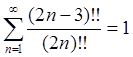. (97)

При : 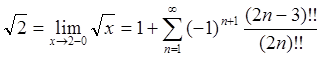. Здесь для установления сходимости ряда достаточно теоремы Лейбница (смотри параграф 15, пример 5).

Таким образом, точный интервал сходимости имеет вид .

Пример 5: Исследовать сходимость ряда Тейлора для функци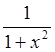и в окрестности точки .

Поскольку 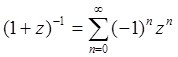(смотри (94e)), полагая , приходим к следующему разложению в ряд Тейлора в окрестности точки : 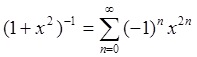. Данный ряд представляет собой сумму членов геометрической прогрессии с параметрами и , и сходится к величине при . При ряд 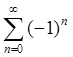расходится. Несмотря на то, что функция является бесконечно дифференцируемой на вещественной оси, она имеет особые точки , которые определяются из уравнения . В соответствии с Т4 радиус сходимости ряда Тейлора равен (смотри рис. 24).