Используя команду рисования точки, выводим кривую на экран.
· Для проверки правильности построения на экран выводятся узлы интерполяции и значения в этих узлах.
1.2. Аппроксимация функции
Постановка задачи:
Дан набор точек на плоскости (xi, yi), i = 1, …, n. Необходимо найти прямую, наименее уклоняющуюся от этих точек. Запишем уравнение прямой в следующем виде y = ax + b.
Задача состоит в поиске неизвестных коэффициентов a и b, которые минимизируют сумму квадратов расстояний между проекциями точек (xi, yi) на эту прямую вдоль оси OY.
То есть, находится минимум выражения
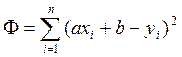
Для этого приравнивают к нулю частные
производные ![]() и
и ![]() ,
получают формулы для нахождения неизвестных коэффициентов
,
получают формулы для нахождения неизвестных коэффициентов
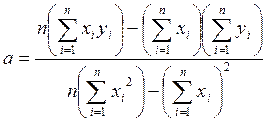 (*)
(*)
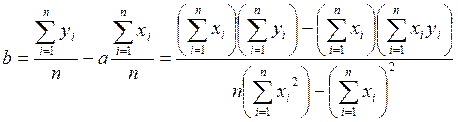 (**)
(**)
Алгоритм:
· В программе задаются функции х(i) и y(i).
· В цикле вычисляются значения сумм из формул (*) и (**).
· Затем находим коэффициенты a и b по формулам (*) и (**).
· Составляем формулу прямой y=ax+b.
· Выводим на экран полученное уравнение прямой y=ax+b.
· При построении прямой y=ax+b выполняем масштабирование.
· В стандартном режиме ширина экрана 640 точек, нам необходимо разбить его на отрезок [-5; 5].
· Задается шаг h, с которым мы будем перемещаться от левой границы интервала до правой при построении графика.
· В цикле определяем значения x и y для этой прямой, а также увеличиваем значении по x на заданный шаг h.
· Используя команду рисования точки, выводим прямую на экран.
1.3. Методы поиска точек экстремума функции на отрезке
Пусть дана функция f
(x), для
которой на заданном отрезке [a; b] нужно найти максимальное значение ![]() или минимальное значение
или минимальное значение ![]() и установить, в какой точке x*это экстремальное значение достигается.
и установить, в какой точке x*это экстремальное значение достигается.
1.3.1. Метод золотого сечения
Точки x1, x2 находятся симметрично относительно середины отрезка [a0, b0] и делят его в пропорции золотого сечения, когда длина всего отрезка относится к длине большей его части также, как длина большей части относится к длине меньшей части:
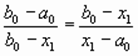 и
и 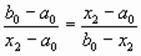 .
.
Отсюда:
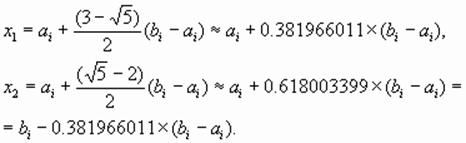
За одну итерацию интервал
неопределенности уменьшается в 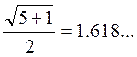 раз, но на следующей итерации
мы будем вычислять функцию только один раз, так как по свойству золотого
сечения
раз, но на следующей итерации
мы будем вычислять функцию только один раз, так как по свойству золотого
сечения 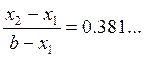 и
и 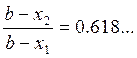 . Для
достижения точности ε потребуется
. Для
достижения точности ε потребуется 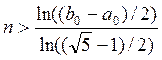 итераций.
итераций.
Алгоритм:
· Необходимо выделить интервал, на котором будет происходить исследование на нахождение точки экстремума.
· По графику определяем приблизительные границы этого интервала.
· С помощью цикла определяются координаты точки экстремума (в нашем случае точки максимума).
· Для ее локализации на графике рисуем окружность небольшого радиуса с центром в точке экстремума.
1.4. Численное интегрирование
Пусть требуется найти интеграл вида
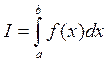 , где
f(x) – непрерывная
функция на отрезке [a,b].
, где
f(x) – непрерывная
функция на отрезке [a,b].
Геометрически, этот интеграл равен площади под графиком функции f(x).
![]()
 y
y
![]() 0 abx
0 abx
Задачей численного интегрирования является построение формул (квадратурные формулы), которые приближённо равны точному значению интеграла. Рассмотрим простейшие квадратурные формулы
Формула трапеций
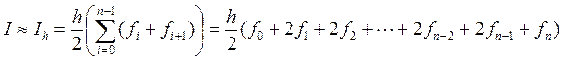 – формула трапеций
– формула трапеций
Алгоритм:
· Задаем интервал, на котором будем проводить интегрирование, для этого левой границе присваиваем значение координаты х точки пересечения графиков, а правой – координату х точки экстремума.
· Задается начальное кол-во разбиений и точность вычисления.
· Затем в цикле происходит вычисление шага, с которым надо двигаться при проведении интегрирования, увеличивается кол-во разбиений (на каждом шаге в 2 раза), и, наконец, вычисляются значения интегралов (точное и приблизительное).
· На экран выводятся точное, приблизительное значения, их разность
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.