Lecture 3
The motion of real fluids is complicated and not yet fully understood. Let us introduce concept of ideal fluid for simplicity of fluids motion understanding. So, flow of an ideal fluid is
steady,
incompressible
nonviscous
and irrotational.
In steady or laminal flow the velocity of the moving fluid at any fixed point does not change with time, either in magnitude or in direction.
The ideal fluid is incompressible. That is, its density has a constant value.
In ideal fluid there isn’t any viscous drag force.
In ideal fluid flow the body will not rotate about an axis through its own center of mass.
The ideal fluid flow characterize by streamlines.
A streamlines is the path traced out by a tiny fluid element, which we may call a fluid “particle”. In the flow we can isolate a tube of flow whose boundary is made up of streamlines. Such a tube acts like a pipe because any fluid particles that enters it cannot escape through its walls.
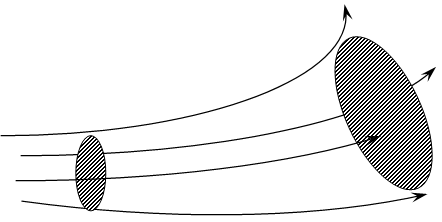


Figure 1 shows two cross sections, of areas A1 and A2, along a tine tube of flow. During the shot time interval Dt, a volume DV of fluid passes trough area A1:
DV=A1v1Dt.
Due to incompressible flow of ideal fluid this volume passes through area A2:
DV=A2v2Dt=A1v1Dt.
Thus along the tube of flow we find
R=Av=constant.
In which R is the volume flow rate. Its SI unit is cubic meter per second.
This equation is called the equation of continuity for fluid flow. It tells us that the flow is faster in the narrower parts of a tube of flow, where the streamlines are closer together.
2. Bernoulli’s equation
Figure 2 represents a tube of flow (or an actual pipe) through which an ideal fluid is flowing at a steady rate. In a time interval Dt, suppose that a volume of fluid DV enters the tube at the left (or input) end and an identical volume emerges at the right (or output) end. The emerging volume must be the same as the entering volume because the fluid is incompressible. By applying the law of conservation of energy to the fluid, you can show truth of the following equation:
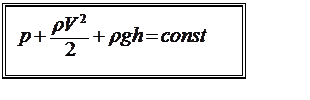
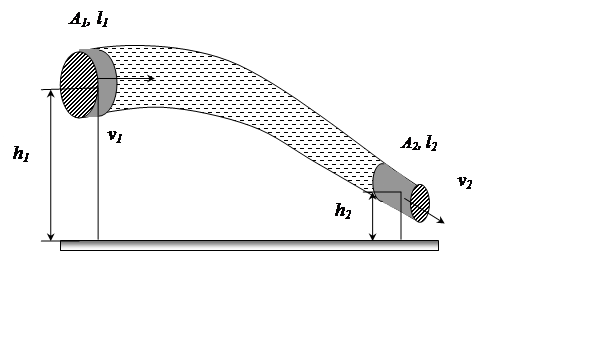 |
Fig. 1. The scheme for Bernoulli’s equation finding.
This equation is called Bernoulli’s equation. It is actually an expression of the law of conservation of mechanical energy in a form more suitable to fluid mechanics.
p represents static pressure (Paskal’s pressure),
rv2/2 is dynamic pressure and rgh represents hydrodynamic pressure.
So, the sum of static, dynamic and hydrostatic pressure in different points of streamline of ideal fluid is constant.
Some applications of Bernoulli’s equation
Horizontal pipe with variable cross-section. The suction-pipe.
Figure 3 represents horizontal pipe with variable cross-section. If h1 = h2 ,so
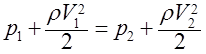 .
.
In the narrower region S2 < S1,so, according to the equation of continuity for fluid flow we have V2 > V1, and according to Bernoulli’s equation we have p2 < p1.
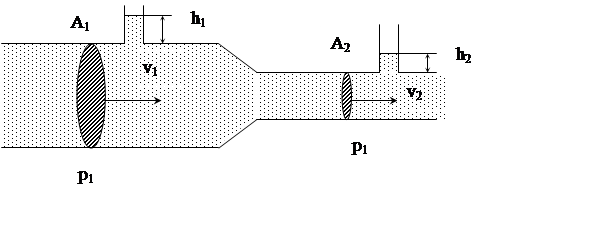
Figure 3.
We can make the pipe with one of its cross-sections will be as narrow as the pressure will be lower than atmospheric. So, The pipe will be suck in an air or a liquid. This phenomenon is used in water-jet pumps, inhalers, and sprayers.
2) Arterial occlusion.
The formation of an atherosclerotic plaque in the artery (The diameter is d1) induces artery narrowing (The diameter is d2).

The blood flow is possible if the static blood pressure Р2 in the point of the formation of atherosclerotic plaque is higher than external pressure (atmospheric pressure) Р0 .
Р2 - Р0 ³ 0.
It realizes if d2³ dmin. (the artery diameter is wider than minimal diameter)
Let us write Bernoulli’s equation and equation of continuity for fluid flow for our case.
![]()
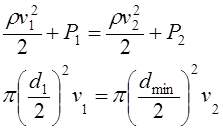
We can take the formula for the minimal diameter
value 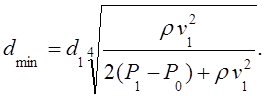
|
For the carotid artery |
Average diameter is equal to d1 = 1 sm, Blood velocity is equal to v1 = 0,2 m/s, Blood density is equal to r = 1,05 × 103 kg/m3, Pressure difference is equal to Р1 - Р0 = 1,33 × 104 Pа |
So calculated value of minimal diameter is dmin » 2 mm.
If artery diameter is narrower than minimal artery diameter the open space of artery will be decrease under the action of the external pressure force. And blood flow will stop. However in organism there are some mechanisms protect against
the arterial occlusion. At narrow arteries the heart works hard and artery pressure increases. So, blood flow will not stop. We can hear the noise accompanied by blood flow through artery with atherosclerotic plaque.
3. The flow of “real” fluids. Viscosity.
All real fluids are viscous, and that property has an important influence on their behavior.
Let us image that in a fluid there are close parallel layers with different speeds. The natural diffusion of molecules caused by their constant random motion will cause some of the molecules from the faster layer to cross into the slower layer. As molecules from the faster stream enter the slower stream, they will be slowed down in a series of collisions, which at the same time will slightly speed up the slower stream. We say that there are drag forces between the layers. These forces are similar to forces of friction for solids. These forces are called forces of viscous friction. It is found experimentally that the force of viscous friction is proportional to product of gradient of velocity and area of layer.
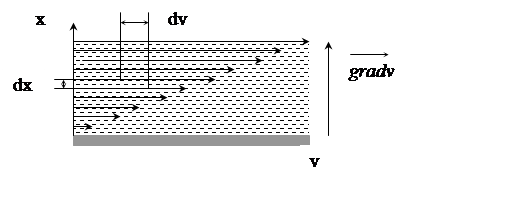 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.