Тепловое излучение. Формула Резерфорда. Распределение электронов в атоме по энергетическим уровням. Рентгеновский спектр, страница 4

Для того, чтобы различные динамические переменные могли одновременно иметь определённые численные значения, необходимо и достаточно, чтобы соответствующие им операторы были коммутирующими.

1.  Пусть  и . Тогда  и .

2.  Пусть  и . Тогда  – собственная функция , т.к. собственные функции отличаются на постоянный множитель.

Одномерная потенциальная яма

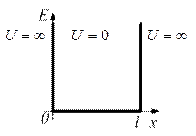Пусть потенциальная энергия частицы задаётся функцией 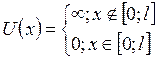 и где-то находится частица. Тогда её волновая функция подчиняется уравнения Шредингера: 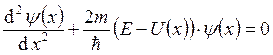. В областях, где  частица находится не может, так как чтобы она туда попала, нужна бесконечно большая энергия. Тогда  при . В других областях . Тогда это уравнение можно записать так: 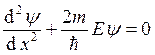. Характеристическое уравнение: 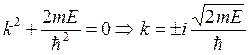. Решение уравнения: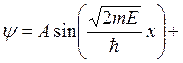 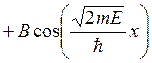 . Волновая функция должна быть непрерывной, следовательно,  и  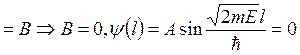. Отсюда следует, что либо , либо 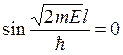. Но, если , то , т.е. частицы нет нигде, что противоречит условию. Следовательно, 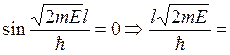 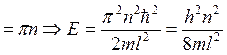, где n – целые числа, причём , т.к. при  и . Константа A определяется из условия нормировки: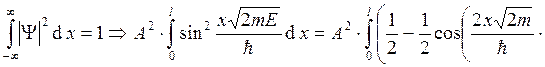  

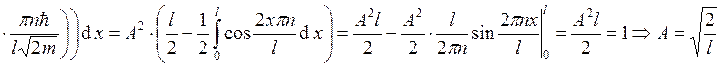
Таким образом, , где .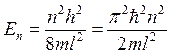

Рассмотрим процесс налетания частицы на потенциальный барьер. Пусть сначала энергия частицы . Уравнение Шредингера для этого случая: 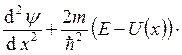 . Оно преобразуется в два: 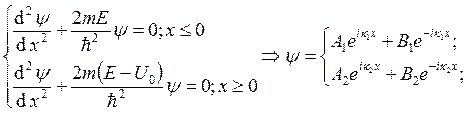 , где 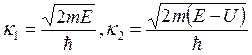. В этой функции слагаемые с положительными степенями описывают частицу, бегущую вправо, а с отрицательными – влево, причём первое уравнение – до столкновения с потенциальным барьером, а второе – после. Частица полностью проходит сквозь барьер, следовательно, , т.к. эта часть описывает частицу, движущуюся влево после столкновения, чего быть не может, так как энергия частицы достаточно велика для прохождения сквозь барьер. Волновая функция должна быть непрерывна: 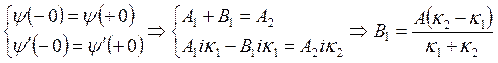. Коэффициент отражения .

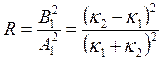Пусть теперь . Тогда уравнение Шредингера будет таким: 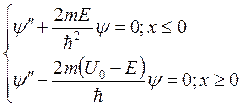, следовательно, 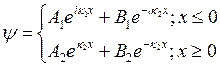. , т.к. . При этом есть вероятность того, что частица пройдёт сквозь барьер, если он конечной длины. Коэффициент прохождения , где l – область барьера.

Квантовогармонический осциллятор

Пусть потенциальная энергия изменяется по закону 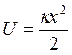. Тогда уравнение Шредингера: .

Движение частицы называется финитным, если оно происходит в конечной области пространства.

Существует общая теорема квантовой механики, согласно которой энергия всегда квантуется у тех систем, движение которых финитно, но может изменяться непрерывно в случае инфинитного движения.

Разность энергий между уровнями: 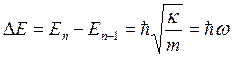, где w – частота частицы. Минимальная энергия – .

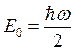Принцип соответствия: Любая новая теория, более общая, чем общепринятая, должна переходить в старую в тех условиях, в которых старая теория была построена и проверена на опыта.

Атом водорода

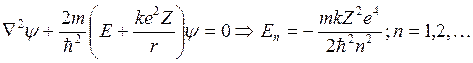, если .

Собственные функции электрона в атоме водорода содержат три целочисленных параметра:  – главное квантовое число,  – азимутальное квантовое число,  – магнитное квантовое число. Состояния, обладающие одинаковой энергией и разными квантовыми числами, называют вырожденными. Число различных состояний для данного  называется кратностью вырождения. Она равна .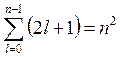

Проекция момента импульса

Найдём собственные значения оператора момента импульса, т.е. решим уравнение . В цилиндрической системе координат 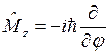, где j – полярный угол. Тогда это уравнение записывается в виде: 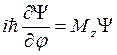. Путём подстановки можно проверить, что решение этого уравнения – 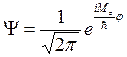 (здесь  – нормировочный множитель). Из однозначности определения волновой функции следует, что 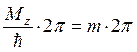, где m – магнитное квантовое число. Тогда . Уравнение, составленное для полного момента имеет конечное и однозначное решение лишь при .

Одновременно можно знать только модуль момента импульса и его проекцию на одну из осей.

Вектор момента импульса никогда не может быть направлен вдоль той оси, проекцию момента импульса на которую мы знаем.

Различные функции Y, соответствующие различным l, соответствуют  электронам с различными моментами импульса.

Говорят, что электрон, у которого , находится в s-состоянии,  – в p-состоянии,  – d,  – f,  – g.