Аджемян Лоран Цолакович
д.т. (812) 428-25-72, м.т. 8-921-778-26-21
Loran.Adzhemyan@pobox.spbu.ru
УДК 536.423.4+531.528
ПЕРЕКОНДЕНСАЦИЯ ПЕРЕСЫЩЕННОГО ПАРА: АНАЛИТИЧЕСКИЕ ТЕОРИИ И ЧИСЛЕННЫЙ ЭКСПЕРИМЕНТ
А.Н.Васильев, А.К.Казанский, Л.Ц.Аджемян
Санкт-Петербургский государственный университет,
физический факультет
198504 Санкт-Петербург, Петродворец, ул. Ульяновская, 1
Поступила в редакцию
Численным интегрированием уравнений движения изучен процесс конденсации пересыщенного пара с момента окончания образования зародышей и до достижения асимптотического режима переконденсации. Проведена проверка аналитических теорий конденсации. Изучена зависимость финального автомодельного распределения капель по размерам от вида их начальной функции распределения в широком диапазоне изменения параметров.
КОНДЕНСАЦИЯ ПЕРЕСЫЩЕННОГО ПАРА ПО ОКОНЧАНИИ СТАДИИ ОБРАЗОВАНИЯ НОВЫХ ЗАРОДЫШЕЙ
Процесс конденсации пересыщенного пара по
окончании стадии образования новых зародышей (капель) описывается системой
уравнений для радиуса капли ![]() , функции распределения
капель по размерам
, функции распределения
капель по размерам ![]() , числовой плотности
пересыщенного пара
, числовой плотности
пересыщенного пара ![]() и связанного с ней соотношением
и связанного с ней соотношением
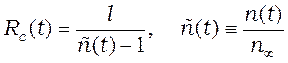 ,(1)
,(1)
критического радиуса капель![]() . Здесь
. Здесь ![]() –
плотность насыщенного пара над плоской границей раздела фаз, параметр
–
плотность насыщенного пара над плоской границей раздела фаз, параметр ![]() определен соотношением
определен соотношением 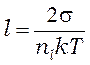 , где
, где ![]() –
коэффициент поверхностного натяжения,
–
коэффициент поверхностного натяжения, ![]() –
плотность жидкости. Соответствующая система уравнений имеет вид [1]:
–
плотность жидкости. Соответствующая система уравнений имеет вид [1]:
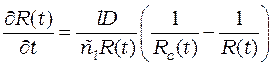 , (2)
, (2)
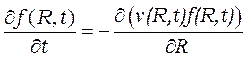 ,
, 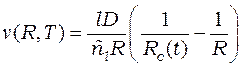 , (3)
, (3)
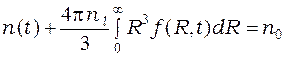 (4)
(4)
Уравнение (2) описывает изменение со временем радиуса капли
в диффузионном режиме поглощения каплей пара, здесь ![]() –
коэффициент диффузии. Уравнение (4) представляет собой условие постоянства
полного числа молекул в единице объема
–
коэффициент диффузии. Уравнение (4) представляет собой условие постоянства
полного числа молекул в единице объема ![]() (пар +
капли). Функция распределения
(пар +
капли). Функция распределения ![]() нормирована так, что
интеграл
нормирована так, что
интеграл
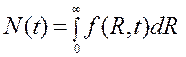 (5)
(5)
дает среднее количество капель в единице объема. Дифференцируя (5) по времени, используя уравнение движения (3) и интегрируя по частям, получаем соотношение
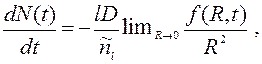 (6)
(6)
определяющее скорость убыли числа капель. Чтобы она была
конечна, необходимо, чтобы функция распределения при малых ![]() имела асимптотику
имела асимптотику
![]() .
(7)
.
(7)
В начале стадии конденсации
пересыщение ![]() заметно превышает единицу и критический
радиус в (2) является малой величиной порядка
заметно превышает единицу и критический
радиус в (2) является малой величиной порядка ![]() (например,
для воды
(например,
для воды ![]() см.). Мы будем считать, что в начальном распределении
см.). Мы будем считать, что в начальном распределении
![]() представлены капли существенно большего
размера. В этом случае в начальной стадии вторым слагаемым в уравнении (2)
можно пренебречь и уравнение (3) для функции распределения имеет явное решение,
которое выглядит наиболее просто, если его сформулировать в терминах
распределения по квадрату радиуса капли
представлены капли существенно большего
размера. В этом случае в начальной стадии вторым слагаемым в уравнении (2)
можно пренебречь и уравнение (3) для функции распределения имеет явное решение,
которое выглядит наиболее просто, если его сформулировать в терминах
распределения по квадрату радиуса капли ![]() – это
распределение сохраняет свою первоначальную форму
– это
распределение сохраняет свою первоначальную форму ![]() ,
смещаясь по времени в сторону больших размеров капель. Такой процесс мог бы
продолжаться до тех пор, пока не будет исчерпан запас избыточного пара, однако
он сопровождается ростом
,
смещаясь по времени в сторону больших размеров капель. Такой процесс мог бы
продолжаться до тех пор, пока не будет исчерпан запас избыточного пара, однако
он сопровождается ростом ![]() и при достаточном
падении пересыщения критический радиус “догоняет” по величине основную массу
капель – начинается процесс переконденсации. Второе слагаемое в (2) становится
существенным: капли с размером больше критического продолжают расти, с размером
меньше критического – уменьшаться в размерах.
и при достаточном
падении пересыщения критический радиус “догоняет” по величине основную массу
капель – начинается процесс переконденсации. Второе слагаемое в (2) становится
существенным: капли с размером больше критического продолжают расти, с размером
меньше критического – уменьшаться в размерах.
В основополагающих работах по
теории переконденсации [2,3] было найдено асимптотическое поведение функции
распределения на больших временах. Согласно этой теории при достаточно больших
временах функция распределения забывает все детали начального распределения,
она носит автомодельный характер и единственным параметром, определяющим ее
зависимость от времени, является текущий критический радиус ![]() :
:
![]() ,
, ![]() , (8)
, (8)
где ![]() –
универсальная функция безразмерного радиуса
–
универсальная функция безразмерного радиуса ![]() :
:
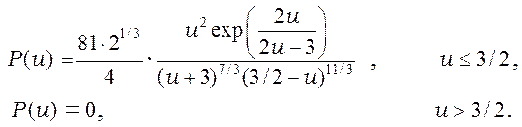 (9)
(9)
Функция ![]() (8) с
(8) с ![]() из (9) является точным решением уравнения
(3), если критический радиус степенным образом зависит от времени
из (9) является точным решением уравнения
(3), если критический радиус степенным образом зависит от времени
![]() ,
(10)
,
(10)
этому соответствует асимптотическое убывание пересыщения пара по закону
![]() . (11)
. (11)
Уравнение баланса вещества (4)
выполнено приближенно, с учетом того, что подавляющая часть избыточного пара
перешла к этому моменту в капли, а интеграл (4) с функцией (8) не зависит от
времени, при этом постоянная ![]() в (8) выбирается из
условия
в (8) выбирается из
условия
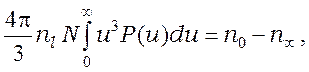 (12)
(12)
откуда, с учетом (9),
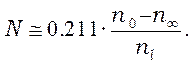 (13)
(13)
В теории Лифшица-Слезова [2,3] доказана “локальная устойчивость” асимптотического решения (8)–(10), проявляющаяся в том, что если система приблизилась к данному асимптотическому режиму, то поправки к нему будут малы. Это не означает, однако, устойчивости решения по отношению к вариациям начальных данных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.