Дисконтирование по учетной ставке используется при учете банком векселей, в этом случае формула (3) будет иметь следующий вид:
S (o) = S(T) (1 – dn),
где S (o) – сумма, выплаченная владельцу векселя банком;
S (T)–обязательство по векселю, которое должно быть погашено в срок Т;
n– срок от момента учета до даты погашения векселя.
Доход (дисконт), который имеет банк от операции учета векселя определяется как разница между обязательством по векселю и ценой покупки:
D (n) = S (T) – S (o) = S (T)d n.
Учет векселей — это покупка их банком, в результате чего они полностью переходят в его распоряжение, а вместе с ними и право требования платежа от векселедателей. Поскольку векселедержатель, предъявивший банку векселя к учету, получает по ним платеж немедленно, т. е. до истечения срока платежа по векселю, то для него фактически это означает получение кредита от банка. Поэтому учет векселей третьих лиц банками — один из способов предоставления ссуд. За такую операцию банк взимает процент, который называется учетным процентом, или дисконтом. Его величина определяется по договоренности с клиентом в зависимости от срока, оставшегося до наступления срока платежа по векселю. Учетный процент удерживается банком из суммы векселя сразу же, в момент его учета (покупки).
Учетный процент представляет собой плату за предоставленные векселедержателю кредитные ресурсы банка. Он определяется на основе ставки рефинансирования Центрального банка РФ или исходя из действующих в данном банке ставок кредитов подобной продолжительности (период с даты учета до даты погашения векселя).
Суммарный доход банка от учета векселей (дисконт) складывается из учетного процента и банковской комиссии, которая включает потенциальные рисковые потери по конкретному векселю, а также дополнительные расходы банка по погашению векселя или его протесту в случае нарушения сроков погашения.
Пример 4.
Тратта (переводной вексель) выдан на сумму 1 млн. руб. с уплатой 17.11.95г. Владелец векселя учел его в банке 23.09.95г. по учетной ставке 20%. Определить сумму, уплаченную владельцу векселя и дисконт банка.
Решение:
Используем формулу дисконтирования по учетной ставке.
S (o) = 1000000 (1- 0,2 × ![]() ) = 969444,5 (руб.)
) = 969444,5 (руб.)
D (T) = 1000000 – 969444,5 = 30555,5 (руб.)
Пример 5.
Через 180 дней после подписания договора должник уплатит 310 тыс. руб. Кредит выдан под 16% годовых. Какова первоначальная сумма долга при условии, что временная база равна 365 дней?
Решение:
Используем формулу математического дисконтирования.
S
(o) = 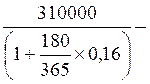 = 287328,59 (руб.)
= 287328,59 (руб.)
Дисконт равен: D (T) = 310000 – 287328,59 = 22671,41 (руб.)
1.3. Наращение по учетной ставке
Из формул дисконтирования легко вывести формулу наращения по учетной ставке:
S(T) = S(o)
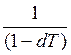
Как видно, учетная ставка не может принимать любое значение, необходимо, чтобы выполнялось неравенство (1 – dT) > 0, или d < 1/T.
На практике учетные ставки применяются при учете векселей банком.
Формулы дисконтирования по процентной и учетной ставкам приведены в соответствующей таблице Справочника.
Теория процентных ставок нашла широкое применение в банковских операциях, например, при учете векселей или выдачи ссуды. В частности на основе приведенных формул можно составить план погашения задолженности. Рассмотрим задачу погашения кредита в рассрочку равными суммами .
Пример 6.
Пусть кредит 250000 руб. выдан на пять лет под 30% годовых. Долг погашается равными частями, проценты начисляются на оставшуюся сумму долга один раз в год и выплачиваются вместе в выплатой основного долга.
Решение:
В данном примере ежегодная сумма погашения долга равна 50000 руб. В первый год будут начислены проценты в размере 250000х0,3=75000(руб.) и сумма, подлежащая уплате составит 125000 руб. Во втором году остаток долга составит 200000 руб., на него начисляются проценты в сумме 60000 руб. и сумма, подлежащая уплате, составит 110000 руб. Для третьего года и последующих лет расчеты проводятся аналогично. План погашения займа можно оформить в виде таблицы 1.
Таблица1.
План погашения кредита равными суммами (руб.)
|
Год |
Остаток долга |
Погашение основного долга |
Проценты |
Срочная уплата |
|
1 |
250000 |
50000 |
75000 |
125000 |
|
2 |
200000 |
50000 |
60000 |
110000 |
|
3 |
150000 |
50000 |
45000 |
95000 |
|
4 |
100000 |
50000 |
30000 |
80000 |
|
5 |
50000 |
50000 |
15000 |
65000 |
|
Итого: |
- |
250000 |
225000 |
475000 |
Как видно из таблицы 1 сумма начисленных процентов включается ежегодно в сумму, подлежащую уплате и общая сумма выплат составит 475000 руб.
Контрольные вопросы
1. Дайте определение процентной ставки. Как с помощью процентной ставки определить сумму начисленных процентов?
2. Что такое конверсионный период? Какой период времени может быть выбран в качестве конверсионного периода?
3. Дайте характеристику декурсивному и антисипативному способу начисления процентов.
4. В чем сущность наращения по простым процентам? Выведите формулу наращения по простым процентам.
5. В чем сущность дисконтирования по простым процентам? Назовите различие между математическим дисконтированием и банковским учетом.
ТЕМА2. СЛОЖНЫЕ ПРОЦЕНТЫ
Во второй теме рассмотрены вопросы теории сложных процентов. Основная цель данной темы – показать отличие простых процентов от сложных и обосновать возможность применения формул наращения по сложной процентной ставке в финансовых расчетах. Здесь рассмотрены следующие вопросы:
1. Начисление процентов по сложной годовой процентной ставке. Капитализация процентов. Переменные ставки сложных процентов.
2. Начисление процентов m раз в году. Номинальная и эффективная ставки процентов.
3. Сравнение простых и сложных процентов.
4. Дисконтирование по сложной процентной ставке.
5. Дисконтирование по сложной учетной ставке.
6. Наращение по сложной учетной ставке.
2.1. Начисление процентов по сложной годовой процентной ставке
В средне- и долгосрочных финансово-кредитных операциях, если проценты не выплачиваются сразу после их начисления, а присоединяются к сумме долга, для наращения применяют сложные проценты. База для начисления сложных процентов (в отличие от простых) не остается постоянной – она увеличивается с каждым шагом во времени, абсолютная сумма начисленных процентов возрастает и процесс увеличения суммы долга происходит с ускорением. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, называют капитализацией процентов.
Формула наращения годовых сложных процентов (проценты начисляются и капитализируются один раз в году) имеет следующий вид:
S (T) = S (o) (1 + i)T (4)
Проценты за этот же период равны:
I = S (T) – S (o) = S (o) [(1 + i)T - 1].
Иногда в расчетах используются переменные ставки
сложных процентов за отдельные периоды времени. В этом случае множитель
наращения имеет следующий вид: (1 + i1)n![]() (1 + i2)n
(1 + i2)n![]() … (1 + ik)n
… (1 + ik)n![]() ,
,
где i1, i2, … , ik – последовательные во времени значения ставок;
n1, n2, … , nk – периоды, в течение которых действуют соответствующие ставки.
Обозначим qm – процентную ставку для которой срок начисления меньше года и за год начисление процентов происходит m раз. Тогда наращенная сумма определяется по формуле S(T) = S(o) (1 + qm). Например, месячная ставка равна 3%, тогда за год множитель наращения составляет (1 + 0,03)12 = 1,43, т.е. первоначальный капитал увеличится в 1,43 раза.
Зная годовую процентную ставку можно определить ставку процентов за месяц, квартал и т.д. Например, годовая ставка сложных процентов равна 60%. Для того, чтобы определить месячную ставку iмес. приравняем множители наращения:
(1 + iмес)12 = (1 + 0,6).
Из данного равенства найдем iмес. = (1,6)1/12 – 1 = 4%. Ставка процентов за квартал составляет iкв. = (1,6)1/4 – 1 = 12,5%. Процентная ставка за полугодие равна (1,6)1/2 – 1 = 26,5%.
Если срок финансовой операции Т – не является целым числом, то возможен смешанный метод расчета наращенной суммы. В соответствии с ним начисление процентов за целое число лет идет по формуле сложных процентов, а за дробную часть периода по формуле простых процентов:
S (T) = S (o) (1 + i)[T] (1 + i{T}),
где [T] – целая часть Т; {T} – дробная часть Т.
Пример 7.
Первоначальная сумма долга равна 50000000 руб. Определить наращенную сумму через 2,5 года, если используется ставка сложных процентов 25% годовых.
Решение:
Используя формулу (4) имеем:
S (T) = 50000000 (1 + 0,25)2,5 = 87346390 (руб.)
Смешанный метод расчетов дает другой результат:
S (T) = 50000000 (1 + 0,25)2 (1 + 0,25 × 0,5) = 87890625 (руб.).
2.2. Начисление процентов m раз в году
Начисление сложных процентов может осуществляться
несколько раз в году. В этом случае используется номинальная ставка
процентов iH. Это годовая ставка, для которой фиксируется число
периодов начисления в году, например, раз в квартал, раз в полугодие и т.д.
Обозначим это число через m. Тогда за соответствующий период ![]() начисление идет по ставке
начисление идет по ставке ![]() .
.
![]() Наращенная
сумма по номинальной ставке процентов определяется по формуле:
Наращенная
сумма по номинальной ставке процентов определяется по формуле:
![]()
![]() S (T)
= S (o) (1 +
S (T)
= S (o) (1 + ![]() )mT.
)mT.
Очевидно, что чем больше m, тем больше сумма начисленных процентов.
Пример 8.
10 млн. руб. инвестированы на два года по ставке 120% годовых. Требуется найти наращенную сумму за два года, если начисление процентов производится: а) ежегодно; б) по полугодиям; в) ежеквартально; г) ежемесячно.
Решение:
а) m = 1 S (T) = 10000000 (1 + 1,2)2 = 48400000 (руб.)
б) m
= 2 S (T) = 10000000 (1 + ![]() )4
= 65536000 (руб.)
)4
= 65536000 (руб.)
в) m
= 4 S (T) = 10000000 (1 + ![]() )8
= 81573072 (руб.)
)8
= 81573072 (руб.)
г) m = 12 S (T)
= 10000000 (1 + ![]() )24 = 98497307 (руб.)
)24 = 98497307 (руб.)
Введем новое понятие - эффективная ставка
процентов. Эта ставка измеряет тот реальный относительный доход, который
получают в целом за год от начисления процентов. Эффективная ставка является
эквивалентной для номинальной ставки в финансовом отношении. Использование
эффективной ставки дает тот же результат что и m-разовое
начисление процентов по ставке ![]() . Формулы для
определения эффективной и номинальной ставок выводятся из равенства множителей
наращения:
. Формулы для
определения эффективной и номинальной ставок выводятся из равенства множителей
наращения:
iэф. = (1 + ![]() )m –
1
)m –
1
IH = m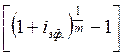 .
.
Две номинальные годовые ставки называются эквивалентными, если соответствующие им годовые ставки совпадают.
Пример 9.
Банк начисляет проценты на вклады по номинальной ставке сложных процентов 12% годовых. Определить доходность вкладов по эффективной ставке процентов при начислении: а) по полугодиям; б) ежеквартально; в) ежемесячно.
Решение:
а) iэф.
= (1 + ![]() )2 – 1 = 0,1236 iэф. = 12,4%
)2 – 1 = 0,1236 iэф. = 12,4%
б) iэф.
= (1 + ![]() )4 – 1 = 0,1255 iэф. = 12,6%
)4 – 1 = 0,1255 iэф. = 12,6%
в) iэф.
= (1 + ![]() )12 – 1 = 0,1268 iэф. = 12,7%
)12 – 1 = 0,1268 iэф. = 12,7%
Таким образом, использование годовой ставки 12,4% дает ту же сумму начисленных процентов, что и номинальная ставка 12% при их начислении по полугодиям.
2.3. Сравнение простых и сложных процентов
В таблице приведены множители наращения по простым и сложным процентам при ставке 8% годовых и временной базе 365 дней.
|
Множитель |
Срок ссуды |
||||||
|
наращения |
30 дней |
180 дней |
1 год |
5 лет |
10 лет |
50 лет |
100 лет |
|
1 + iT |
1,00657 |
1,0394 |
1,08 |
1,4 |
1,8 |
5,0 |
9,0 |
|
(1 + i)T |
1,00635 |
1,0392 |
1,08 |
1,47 |
2,16 |
46,9 |
2199,8 |
При сроке 1 год множители наращения совпадают и равны 1 + i. Для остальных выполняются неравенства: (1 + iT) > (1 + i)T при 0 < Т < 1; (1 + iT) < (1 + i)T при Т > 1. Поэтому в долгосрочных операциях как правило используются сложные проценты.
2.4. Дисконтирование по сложной процентной ставке
Формула математического дисконтирования по сложной ставке процентов выводится из формулы (4):
S
(o) = 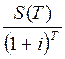
и для номинальной ставки:
S
(o) = 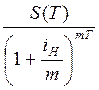 .
.
Величину S(o), полученную дисконтированием S(T) называют современной величиной или современной стоимостью S (T). Разность суммы D = S(T) – S(o), в случае, когда S(o) определено дисконтирование называют дисконтом.
2.5. Дисконтирование по сложной учетной ставке
Дисконтирование по сложным учетным ставкам осуществляется по формулам:
S (o) = S (T) (1 - d)T
S (o) = S (T) (1 - ![]() )mT ,
)mT ,
где d – годовая сложная учетная ставка; dH – номинальная учетная ставка, по которой дисконтирование производится m раз в году. Дисконтирование по сложной учетной ставке происходит с замедлением, так как каждый раз учетная ставка применяется не к первоначальной сумме (как при простой учетной ставке), а к сумме, уже дисконтированной на предыдущем шаге во времени.
2.6. Наращение по сложной учетной ставке
Антисипативный способ начисления сложных процентов предполагает использование учетной ставки по формуле:
S
(T) = S (o)
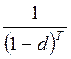 .
.
Множитель наращения в этом случае имеет вид 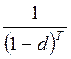 .
.
Пример 10.
Определить наращенную на 10000 руб. сумму за 6 лет при использовании:
а) ставки простых процентов 10% годовых;
б) ставки сложных процентов 10% годовых;
в) простой учетной ставки 10% годовых;
г) сложной учетной ставки 10% годовых.
Решение:
а) S (T) = 10000 (1 + 0,1 × 6) = 16000 (руб.); I (T) = 6000 (руб.)
б) S (T) = 10000 (1 + 0,1)6 = 17716 (руб.); I (T) = 7716 (руб.)
в) S (T) = 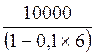 = 25000 (руб.); I
(T) = 15000 (руб.)
= 25000 (руб.); I
(T) = 15000 (руб.)
г) S (T) = 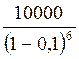 = 18816 (руб.); I
(T) = 8816 (руб.)
= 18816 (руб.); I
(T) = 8816 (руб.)
Как видно из примера, наибольший рост капитала будет при начислении процентов по простой учетной ставке (на практике она не применяется на длительных, больше года, периодах начисления).
Формулы наращения и дисконтирования по процентной и учетной ставкам приведены в соответствующей Таблице Справочника ЭУМК.
Контрольные вопросы
1. В чем отличие начисления сложных процентов от начисления простых процентов?
2. Дайте определение номинальной ставки процентов. В каких случаях она используется?
3. Выведите формулы математического дисконтирования по сложным процентам.
4. Поясните смысл утверждения, что «начисление по сложным процентам идет с ускорением».
5. В каких финансовых операциях используются сложные и простые проценты?
ТЕМА 3. ЭКВИВАЛЕНТНОСТЬ ПРОЦЕНТНЫХ СТАВОК
В третьей теме рассмотрено понятие эквивалентности процентных ставок Основная цель данной темы– дать представление об эквивалентности процентных ставок и показать возможности использования процентных ставок разного вида в финансовых расчетах.
Здесь излагаются следующие вопросы:
1. Эквивалентность простых процентных ставок.
2. Эквивалентность простых и сложных ставок.
3. Эквивалентность сложных ставок.
Эквивалентные процентные ставки – это такие процентные ставки разного вида, применение которых при равных начальных условиях дает одинаковые финансовые результаты. Замена одной ставки на другую при соблюдении принципа эквивалентности не изменяет финансовых последствий операции. Формулы эквивалентности выводятся из равенства множителей наращения.
3.1. Эквивалентность простых процентных ставок
Если временные базы для учетной и процентной ставок
одинаковы, то из равенства (1 + iT) = 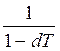 получаются
соответствующие формулы:
получаются
соответствующие формулы:
i
= 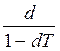 ; d
=
; d
= 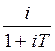 .
.
Если срок операции Т выражается в днях, то формулы имеют вид:
а) К = 360 дней
i
= 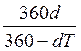 ; d
=
; d
= 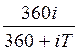 .
.
б) если при начислении процентов принята временная база К = 365, для учетной ставки К = 360, то
i
= 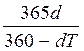 ; d
=
; d
= 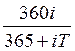 .
.
Пример 11.
Банк использует при выдаче кредитов ставку 12% годовых. Определите значение учетной ставки, обеспечивающей равную доходность при учете векселя, до срока погашения которого осталось 50 дней, если расчетное количество дней в году при начислении процентов по кредитам равно 365, а при учете векселей – 360.
Решение:
d
= 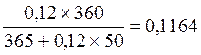 (11,64%).
(11,64%).
i
= 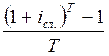 ; iсл. = (1 - Td)1/T – 1.
; iсл. = (1 - Td)1/T – 1.
Для простой учетной ставки и сложной процентной ставки из равенства соответствующих множителей наращения имеем формулы:
i
= 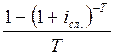 ; iсл. = (1 - Td)-1/T – 1.
; iсл. = (1 - Td)-1/T – 1.
Пример 12.
Ссуда выдана под 20 сложных годовых процентов. Каков должен быть уровень простой ставки (К = 365) при сроке 6 месяцев.
Решение:
i
= 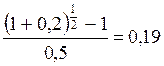 (19%).
(19%).
3.3. Эквивалентность сложных ставок
Для сложной и учетной ставок соответствующие формулы имеют вид:
iсл. = 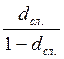 ; dсл. =
; dсл. = 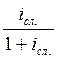 .
.
Пример 13.
Какова должна быть сложная учетная ставка d, чтобы сумма 10 000 руб., вложенная в эту ставку на 2 года, достигла той же величины, что и сумма 15 000 руб., вложенная под сложную ставку ссудного процента 10 % на 3 года.
Решение:
Поскольку финансовые результаты (наращенные суммы) в обоих случаях должны быть равны, можно записать
15000 (1 + 0,1)3 = 10000 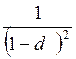
Из этого уравнения найдем d
d
= 1 - 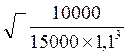 =
29,2 %
=
29,2 %
Принцип эквивалентности широко используется в практических задачах и облегчает расчеты. Рассмотрим следующий пример.
Пример 14.
Определить, под какую процентную ставку процентов выгоднее поместить капитал 20 000 руб. на 3 года: а) под простую ставку процентов 20 % годовых б) под сложную ставку процентов 10 % годовых с ежеквартальным начислением процентов?
Решение:
В данной задаче можно рассчитать наращенные суммы в обоих случаях:
а) S(3) = 20 000 × (1 + 0,2 × 3) = 32 000 (руб.)
б) S(3) = 20 000 × (1 + ![]() )12 = 26 889 (руб.)
)12 = 26 889 (руб.)
Более выгодно использовать ставку простых процентов 20 % годовых. Данный пример можно упростить с помощью использования формул эквивалентности. Найдем простую ставку процентов, которая является эквивалентной для номинальной ставки:
i
= [(1 + ![]() )12
– 1] / 3 = 11,48 %
)12
– 1] / 3 = 11,48 %
Как видно, данная ставка значительно ниже 20 % и, следовательно, обеспечивает меньшую доходность. Необходимо выбрать простую процентную ставку 20 % годовых.
Найдем номинальную процентную ставку с ежеквартальным начислением, которая бы обеспечила равную доходность, что и простая ставка 20 % годовых. Для этого рассчитаем номинальную ставку сложных процентов с ежеквартальным начислением по соответствующей формуле эквивалентности:
iH = [(1 + 0,2 × 3)1/12 – 1] × 4 = 16 %
Таким образом, для обеспечения равной доходности необходимо использовать номинальную ставку 16 % с ежеквартальным начислением процентов. Использование номинальной ставки 10 % с ежеквартальным начислением процентов, как мы видели, дает меньший эффект.
Понятие финансовой эквивалентности и эквивалентных процентных ставок имеют большое практическое применение в финансовых расчетах. Например, оценка доходности различных финансовых операций проводится с помощью годовой процентной ставки.
Рассмотрим два примера по оценке доходности финансовых операций.
Пример 15.
По вкладу А проценты начисляются четыре раза в год исходя из 5% в квартал. По вкладу Б начисление процентов осуществляется по полугодиям исходя из процентной ставки 22% годовых. Необходимо сравнить доходности размещения средств.
Решение:
По вкладу А начисление процентов идет по номинальной ставке 20%, а по вкладу Б – по номинальной ставке 22% годовых. Однако число начислений процентов в году по варианту А и Б различно. Оценим доходность с помощью годовой ставки сложных процентов.
Вклад А: i= (1+0,05)4-1=0,216
Вклад Б: i=(1+0,11)2-1=0,232
Как видно эффективная процентная ставка по варианту Б выше (23,2%), чем по варианту А (21,6%), следовательно, более выгодным является размещение денежных средств по вкладу Б.
Пример 16.
Что выгоднее:
а) приобрести дисконтный вексель со сроком обращения 180 дней при использовании учетной ставки 40% годовых;
б) предоставить ссуду на тот же срок под 30% годовых с начислением процентов по полугодиям.
Решение:
Оценим доходность финансовых операций по двум вариантам. Для этого рассчитаем с помощью формулы эквивалентности ставку простых процентов:
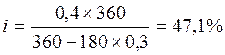
а) б) i = (1+0,15)2-1=32,25%
Как видно из расчетов доходность, выраженная в виде годовой ставки простых процентов выше по варианту а), следовательно, вариант а) является более выгодным.
Контрольные вопросы
1. Какие процентные ставки называются эквивалентными?
2. Как выводятся формулы эквивалентности?
3. В каких случаях возможна замена одной процентной ставки на другую.
4. Выведите формулы эквивалентности для простой процентной ставки и номинальной процентной ставки.
5. Выведите формулы эквивалентности для сложной годовой учетной ставки и номинальной учетной ставки.
ТЕМА 4. НАЧИСЛЕНИЕ ПРОЦЕНТОВ И ИНФЛЯЦИЯ
В четвертой теме рассмотрены вопросы, связанные с обесцениванием денег при инфляции. Основная цель данной темы заключается в том, чтобы обосновать использование математики сложных процентов для описания инфляции. Проблема инфляции в здесь рассматривается с двух точек зрения: обесценивание денег при инфляции и защита от инфляции.
Инфляция является объективным фактором, присущим развитию экономики не только нашей страны, но и зарубежных стран. В странах с развитой экономикой – США, Японии, ФРГ, Великобритании, Франции и других – инфляционные процессы происходят непрерывно, хотя их интенсивность относительно низкая.
Инфляция характеризуется обесценением национальной валюты (т.е. снижением ее покупательной способности) и общим повышением цен в стране. В различных случаях влияние инфляционного процесса сказывается неодинаково. Так, если кредитор (инвестор) теряет часть дохода за счет обесценения денежных средств, то заемщик может получить возможность погасить задолженность деньгами сниженной покупательной способности.
Инфляцию необходимо учитывать по крайней мере в двух случаях: при расчете наращенной суммы денег и при измерении реальной эффективности (доходности) финансовой операции.
Обозначим Ip – индекс цен(индекс инфляции) за период времени от t0 до T
Ip = 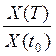 ,
,
где X(T), X (t0) – цены в соответствующие периоды времени.
Обозначим H – темп инфляции за период от t0до T(в %)
H
= 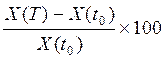 (%).
(%).
Индекс цен и темп инфляции связаны соотношением:
H = (Ip - 1)×100
Ip = ![]() +
1.
+
1.
Индекс цен Ip
показывает во сколько раз выросли цены за период, а темп инфляции – на сколько
процентов выросли цены. Например, за два года цены выросли на 130%. Индекс цен
Ip = ![]() +
1 = 2,3, т.е. цены за два года
выросли в 2,3 раза.
+
1 = 2,3, т.е. цены за два года
выросли в 2,3 раза.
Темп инфляции по своей математической природе аналогичен ставке процентов i, а рост цен аналогичен начислению сложных процентов, так как приращение цены идет к цене в предшествующем периоде. Поэтому для описания инфляции можно использовать математику сложных процентов.
Обозначим ht – темп инфляции
за срок t. Тогда за весь период ![]() множитель
наращения будет равен
множитель
наращения будет равен 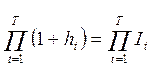 .
.
Индекс инфляции Ip за весь период равен произведению индексов цен за соответствующие периоды. Например, помесячный рост цен составил 25%, 20%, 18%, тогда индекс инфляции за три месяца определяется как
Ip = 1,25 × 1,2 × 1,18 = 1,77 ,
т.е., за три месяца цены выросли в 1,77 раза или на 77%. Предположим, что темп инфляции – постоянная величина. Обозначим через h – годовой (месячный) темп инфляции, тогда за срок T индекс цен равен
Ip = 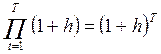 .
.
Например, месячный темп инфляции составляет 10%, тогда за год
Ip = (1 + 0,1)12 = 3,138 Н = (3,138 - 1) ×100 = 213,8%,
т.е., за год цены выросли в 3,138 раза или на 213,8%.
Вернемся к проблеме обесценения денег при их наращении. В общем случае можно записать:
С = ![]() ,
,
где S – наращенная сумма денег, измеренная по номиналу;
С – эта же сумма денег с учетом ее обесценения.
Рассмотрим случай, когда наращение идет по простым процентам.
С = 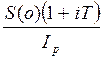 .
.
Пример 17.
На сумму 1500 руб. в течение трех месяцев начисляются простые проценты по ставке 18% годовых (К = 360). Определить реальные результаты, если месячная инфляция составляет 10%.
Решение:
С = 1500 × 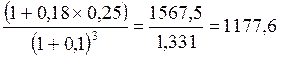 (руб.)
(руб.)
Как видно происходит обесценение капитала.
Если наращение идет по сложной ставке процентов, то сумма денег с учетом их обесценения составит:
С = 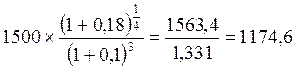 (руб.)
(руб.)
Определим процентную ставку, которая компенсирует инфляцию. Для простых процентов приравняем множитель наращения к 1.
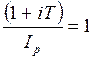 .
.
Обозначим искомую процентную ставку i*
i*
= 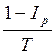 .
.
Для сложных процентов i* = h. Ставку, превышающую i* называют положительной ставкой процента.
Например, в примере 17 для простых процентов
i*
= 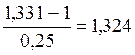 или
132,4%,
или
132,4%,
т.е., процентная ставка выше i* = 132,4% годовых обеспечит реальный доход финансовой операции. Для сложных процентов годовая процентная ставка i*=(1 + 0,1)12 –1 = 213,8%.
В целях защиты от обесценения денег используются различные методы. Наиболее распространенным является корректировка ставки процентов, по которой осуществляется наращение, т.е. увеличение ставки на величину так называемой инфляционной премии, иначе говоря, производится индексация ставки. Итоговую процентную ставку называют брутто-ставкой.
Брутто-ставка включает инфляционную премию и обеспечивает заданную доходность финансовой операции при известном темпе инфляции. Брутто-ставка отличается от положительной ставки процентов, так как положительная ставка является пограничной: процентные ставки, превышающие ее, обеспечивают доход от финансовой операции. Брутто-ставка не просто обеспечивает доход при известном темпе инфляции, а обеспечивает заданную доходность.
Рассмотрим методы определения брутто-ставки. В случае простых процентов брутто-ставку (обозначим ее r) определим из равенства
1 + rT = (1 + iT)Ip
r
= 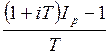 .
.
В случае сложных годовых процентов брутто-ставку определяем из равенства:
1 + r = (1 + i) (1 + h)
r = i + h + i×h.
Например, в примере 17 для простых процентов
r
= 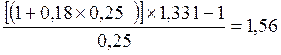 ,
,
т.е. процентная ставка 156% годовых обеспечивает заданную доходность операции 18% годовых при месячном темпе инфляции 10%.
Для случая сложных процентов
r = 0,18 + 2,138 + 0,18 × 2,138 = 2,7 (270%).
Используя ставку 270% годовых можно обеспечить доходность финансовой операции 18% годовых при темпе инфляции 10% в месяц.
Если наращение идет по номинальной ставке сложных процентов с числом начисления процентов в году m раз, то брутто-ставка rH определяется из равенства
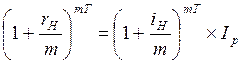
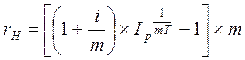 .
.
Пример 18.
Первоначальный капитал в размере 20000000 руб. выдается на три года, проценты начисляются в конце каждого квартала по номинальной ставке 8% годовых. Определить номинальную ставку процентов и наращенную сумму с учетом инфляции, если ожидаемый годовой уровень инфляции составляет 12%.
Решение:
Индекс цен Ip за три года равен (1 + 0,12)3 = 1,4
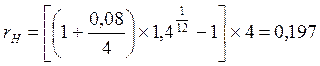
S
(З) = 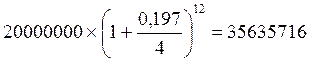 (руб.)
(руб.)
Рассмотрим обратную задачу – измерение реальной ставки процента – т.е. определение i по заданному значению брутто-ставки. Если r – объявленная норма доходности (брутто-ставка), то исходный показатель доходности в виде годовой процентной ставки i можно определить при начислении простых процентов как
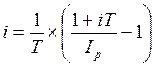 .
.
Аналогичный показатель находится при наращении по сложным процентам:
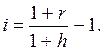
Пример 19.
Определить, какой реальной убыточностью обладает финансовая операция, если при уровне инфляции 14 % в год капитал К вкладывается на один год под номинальную ставку 8 % при ежемесячном начислении.
Решение:
С = К 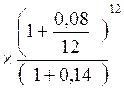 = 0,949 К
= 0,949 К
Таким образом, реальная убыточность финансовой операции составила 5 %. (Первоначальный капитал К уменьшился на 5 %).
Контрольные вопросы
1. Дайте определение индекса инфляции, темпа инфляции. В чем различие между ними?
2. Назовите методы защиты от инфляции.
3. Почему для описания инфляции используется математика сложных процентов?
4. Как определяется брутто-ставка в случае простых процентов (сложных процентов)?
ТЕМА5. ПОТОКИ ПЛАТЕЖЕЙ И ФИНАНСОВЫЕ РЕНТЫ
В пятой теме рассматриваются вопросы теории финансовой ренты, дается понятийный аппарат и вывод основных формул для определения наращенной суммы и современного значения рент постнумерандо и пренумерандо. Основная цель данной темы заключается в том, чтобы показать различные виды рент и для различных рент использовать формулы современного значения и наращенной суммы.
В теме изложены следующие вопросы:
1. Рента постнумерандо (обычная рента). Наращенная сумма постоянной ренты постнумерандо. Современное значение ренты постнумерандо.
2. Рента пренумерандо.
3. Специальные виды рент.
5.1. Рента постнумерандо (обычная рента)
Финансовые операции часто предполагают не разовые платежи, а последовательность платежей во времени. Например, погашение задолженности в рассрочку, периодическое поступление доходов от инвестиций, выплата пенсий и т.д. Такие последовательности платежей называются потоком платежей. Отдельный элемент этого потока называется членом потока. Поток платежей, все члены которого положительные величины, а временные интервалы между платежами одинаковы, называется финансовой рентой(аннуитетом). Рента характеризуется следующими параметрами: член ренты (R) – размер отдельного платежа, период ренты – временной интервал между двумя последовательными платежами, срок ренты (n) – время от начала первого периода ренты до конца последнего периода, процентная ставка (i).
Классификация ренты:
1. По количеству выплат членов ренты на протяжении года ренты делятся на годовые (выплата один раз в году) и p-срочные (p – число выплат в году).
2. По количеству начислений процентов в году ренты делятся на ренты с ежегодным начислением процентов, с начислением mраз в году, с непрерывным начислением.
3. По величине своих членов ренты делятся на постоянные (с одинаковыми платежами) и переменные. Члены переменных рент изменяют свои размеры во времени, следуя какому-либо закону, например, арифметической или геометрической прогрессии, либо несистематично (задаются таблицей).
4. По вероятности выплат ренты делятся на верные (платежи идут в любом случае) и условные (выплаты происходят в зависимости от наступления некоторого случайного события). В случае верной ренты число членов ренты заранее известно. В условной ренте число ее членов заранее неизвестно. Примером условной ренты является пенсионное страхование, когда выплата пенсии производится при достижении установленного возраста.
5. По количеству членов ренты делятся на ренты с конечным числом членов, т.е. ограниченные по срокам и бесконечныеили вечные ренты.
6. По соотношению начала срока ренты и какого-либо момента времени, упреждающего начало ренты (например, начало действия контракта или дата его заключения), ренты делятся на немедленныеи отложенные или отсроченные.
7. По моменту выплат платежей в пределах периода ренты делятся на постнумерандо (если платежи идут в конце периода) и пренумерандо (если платежи производятся в начале периода).
Наращенная сумма постоянной ренты постнумерандо
Наращенная сумма (S) – это сумма всех членов потока платежей с начисленными на них к концу срока процентами.
1. Годовая рента (платежи идут раз в году). Сумма для первого платежа, проценты на который будут начисляться (n - 1) раз составит R(1+i)n-1. Для второго платежа проценты будут начисляться на один год меньше и наращенная сумма составит R (1 + i)n-2. На последний платеж, произведенный в конце n-ого года, проценты не начисляются. Таким образом, поток платежей образует последовательность R(1+i)n-1, R (1 + i)n-2, … , R. Перепишем этот ряд в обратном порядке R, R (1 + i), …, R (1 + i)n-2, R(1+i)n-1
Как видно, он представляет геометрическую прогрессию со знаменателем (1+ i) и первым членом R. Число членов прогрессии равно n. Наращенная сумма S равна сумме членов геометрической прогрессии. Используя формулу для нахождения суммы членов геометрической прогрессии, известную из курса математики средней школы, можно вывести формулу наращенной суммы ренты постнумерандо:
S
= R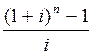 .
.
Множитель 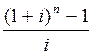 называется
коэффициентом наращения ренты. Значения коэффициентов наращения для
различных i и nприводятся
в специальных таблицах.
называется
коэффициентом наращения ренты. Значения коэффициентов наращения для
различных i и nприводятся
в специальных таблицах.
Аналогично выводятся формулы для других рент.
2. Годовая рента, начисление процентов m раз в году:
S
= R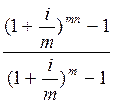 .
.
3. Рента p-срочная начисление процентов 1 раз в год:
S
= R 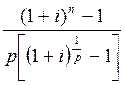 .
.
4. Рента p-срочная, начисление процентов m раз в году (m = p):
S = 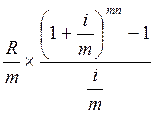 .
.
Пример 20.
Решение:
Рента годовая, постнумерандо, начисление процентов один раз в году, поэтому используем формулу:
S
= R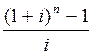 = 40000
= 40000 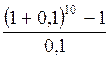 = 63748 (руб.).
= 63748 (руб.).
Пример 21.
Взносы в специальный фонд вносятся в конце каждого квартала с ежеквартальным начислением процентов по номинальной ставке 80% годовых. Определите размер взноса для накопления в течении 5 лет суммы 10 млн.руб.
Решение:
Рента p-срочная постнумерандо (p = 4), начисление процентов 4 раза в году (p = m = 4). Используем формулу:
S = 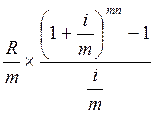 .
.
10000000 = R
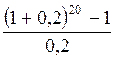 ,
откуда получаем R = 260840,5 (руб.)
,
откуда получаем R = 260840,5 (руб.)
Размер ежегодного взноса составляет 260840,5 руб., размер платежа в квартал – 65210,13 руб.
Современное значение ренты постнумерандо
Под современным значением (А) понимают сумму всех членов ренты, дисконтированных на начало срока ренты или некоторый упреждающий момент времени.
1. Годовая рента постнумерандо
Дисконтированная величина первого платежа равна 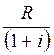 , второго платежа
, второго платежа 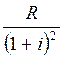 ,
для последнего платежа
,
для последнего платежа 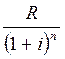 . Как видим эти величины
образуют ряд R (1 + i)-1, R
(1 + i)-2, … , R (1 + i)-n. Сумма
этого ряда определяется по формуле суммы членов геометрической прогрессии
. Как видим эти величины
образуют ряд R (1 + i)-1, R
(1 + i)-2, … , R (1 + i)-n. Сумма
этого ряда определяется по формуле суммы членов геометрической прогрессии
A
= R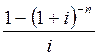 .
.
Аналогично выводятся формулы для других рент.
2. Рента годовая, начисление процентов m раз в году:
A = R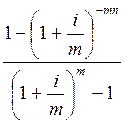 .
.
3. Рента p-срочная, начисление процентов один раз в году
A = R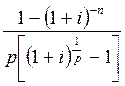 .
.
4. Рента p-срочная, начисление процентов m раз в году (p =m):
A = R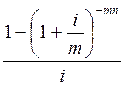 .
.
Пример 22.
Рента постнумерандо характеризуется следующими параметрами: R = 4000 руб., n = 5, i = 18,5% годовых. Определить современную стоимость ренты.
Решение:
Рента годовая, поэтому используем формулу:
A
= R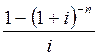 = 4000
= 4000 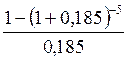 = 12369,7 (руб.)
= 12369,7 (руб.)
То есть все будущие платежи оцениваются в настоящий момент в сумме 12369 руб. Эта сумма обеспечивает ежегодную выплату по 4000 руб. в течении 5 лет.
5.2Рента пренумерандо
Аннуитет пренумерандо предполагает выплату в начале
периода. Различие между рентами постнумерандо и пренумерандо заключается в
числе периодов начисления процентов. Каждый член поступлений из указанных рент
«работает» на один период больше, чем в ренте постнумерано. Обозначим ![]() –
наращенная сумма ренты пренумерандо,
Ä – современное значение ренты пренумерандо. Эти величины определяются
на основе S и A ренты постнумерандо.
–
наращенная сумма ренты пренумерандо,
Ä – современное значение ренты пренумерандо. Эти величины определяются
на основе S и A ренты постнумерандо.
Аннуитет (рента) пренумерандо
|
Наращенная сумма ренты |
Современное значение |
|
|
годовая |
||
|
|
Ä = A (1 + i) |
|
|
годовая, начисление процентов m раз в году |
||
|
|
Ä = A (1 + |
|
|
p-срочная, начисление процентов один раз в году |
||
|
|
Ä = A (1 + i) |
|
|
p-срочная, начисление процентов m раз в году (m = p) |
||
|
|
Ä = A (1 + |
|
Пример 23.
В пенсионный фонд ежегодно в начале года вносятся суммы в размере 25 тыс.руб., на которые начисляются сложные проценты по ставке 3% годовых. Определите сумму, накопленную в фонде через 10 лет и сумму начисленных процентов.
Решение:
Рента пренумерандо, годовая, начисление процентов один раз в год. Используем формулу
S
= S (1 + i) = 25000 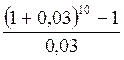
![]() 1,03
= 295194 (руб.)
1,03
= 295194 (руб.)
I = 295194 – 25000 = 270194 (руб.)
Исчисление современной стоимости финансовых рент имеет большее практическое значение, чем вычисление наращенной стоимости. Рассмотрим задачу по оценке инвестиционного проекта.
Пример 24.
В течение 4 лет ожидаются поступления от реализации проекта в размере 2 млн. руб. в конце каждого полугодия. Единовременные вложения в проект в начале первого года составили 10 млн. руб. Будут ли данные вложения убыточны или принесут прибыль, при использовании годовой процентной ставки 6%.
Решение:
Поступления в размере 2 млн. руб. ожидаются в течение четырех лет. Поскольку это разновременные выплаты, необходимо привести их к одной дате. Оценим стоимость этих выплат на начало первого года. Для этого используем формулу современной стоимости р-срочной ренты постнумерандо с начислением процентов один раз в году (См. Справочник, Таблица «Аннуитет постнумерандо».)
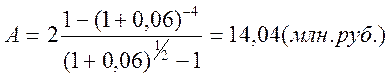
Данный проект можно считать прибыльным, так как вложения 10 млн.руб. обеспечивают ежегодный доход, который на начало первого года оценивается суммой в 14,04 млн. руб.
Теория современной стоимости аннуитета нашла прикладное значение в задачах погашения задолженности равными срочными выплатами. Выше в главе 1 мы уже рассматривали составление плана погашения кредита равными суммами. В данной главе остановимся на задаче погашения задолженности с помощью применения формул финансовой ренты. Экономическая постановка задачи заключается в следующем. Задолженность на начало срока определена в сумме А, ее необходимо погасить равными срочными уплатами R, которые включают в себя начисленные проценты по ставке i. Очевидно, данная задача может быть решена с помощью формул современного значения финансовой ренты.
Пример 25.
Пусть задолженность на текущий момент равна 250000 руб. Долг предлагается погасить в течение 5 лет при использовании процентной ставки 30% годовых. Долг погашается равными срочными уплатами, включающими начисленные проценты. Составить план погашения задолженности.
Решение:
Очевидно, что текущая задолженность 250000 руб. представляет собой современную стоимость финансовой ренты с ежегодными платежами R. Рассчитаем срочные выплаты R на основе формулы современного значения годовой ренты постнумерандо (См. Справочник, Таблица «Аннуитет – постнумерандо»).
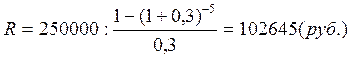
Суммы 102645 руб. выплачиваются в течение пяти лет ежегодно и включают начисленные проценты. Рассчитаем начисленные проценты за первый год:
![]()
Сумма погашения долга в первом году составляет:
102645-75000=27645 (руб.)
Во втором году остаток долга равен:
250000-27645=222355 (руб.)
На эту сумму во втором году начисляются проценты:
![]()
Сумма к погашению во втором году равна:
![]()
Общий план погашения задолженности можно представить в таблице 2.
Таблица 2.
План погашения задолженности равными срочными выплатами (руб.)
|
Год |
Остаток на начало года |
Погашение долга |
Проценты |
Срочная выплата |
|
1 |
250000 |
27645 |
75000 |
102645 |
|
2 |
222355 |
35939 |
66706,5 |
102645 |
|
3 |
186416,5 |
46720 |
55925 |
102645 |
|
4 |
139696,5 |
60736 |
41909 |
102645 |
|
5 |
78960 |
78969 |
23688 |
102645 |
|
Итого: |
- |
250000 |
- |
- |
Контрольные вопросы
1. Дайте определение финансовой ренты. Назовите параметры ренты.
2. В чем отличие ренты постнумерандо от ренты пренумерандо?
3. Приведите примеры финансовых рент.
4. Как определить наращенную сумму постоянной ренты постнумерандо и сумму начисленных процентов?
5. Как определить современное значение постоянной ренты постнумерандо, ренты пренумерандо?
5.3. Специальные виды рент
Рента с выплатами в середине периода
Наращенные суммы и современные стоимости такой ренты находятся умножением соответствующих обобщающих характеристик рент постнумерандо на множитель наращения за половину периода. Например, современную стоимость годовой ренты определим:
А ½ = А (1 + i)½.
Для р-срочной ренты современная стоимость определяется как А ½= А (1 + i)½р.
Отложенные ренты
Все вышеприведенные формулы справедливы для немедленных рент, то есть платежи начинаются сразу в начале (пренумерандо) или конце (постнумерандо) периода. В отложенной (отсроченной) ренте начало выплат сдвинуто относительно некоторого момента времени. Сдвиг во времени никак не отражается на величине наращенной суммы. Определим современную стоимость отложенной ренты (tA). Обозначим t – срок отсрочки выплат, А – современная стоимость на начало выплат. Тогда современная стоимость отложенной ренты tA определяется дисконтированием немедленной ренты А за срок t:
tA = AVt,
где Vt - коэффициент дисконтирования.
Вечная рента
Под вечной рентой понимается ряд платежей, количество которых не ограничено. Наращенная сумма вечной ренты равна бесконечно большой величине. Современная величина вечной ренты (А∞) определяется по следующим формулам:
годовая рента, m =1
А∞ = R /i
годовая рента, начисление процентов m раз в году
А∞ =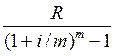
р-срочная рента, m=1
А∞ =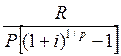 .
.
Современная величина вечной ренты нашла применение в актуарных расчетах, например в пенсионном страховании.
Более глубоко теория финансовой ренты изложена в работах Четыркина Е.М., представленных в Хрестоматии ЭУМК.
Контрольные вопросы
1. Дайте характеристику отложенной ренты. Как определяются наращенная сумма и современная стоимость отложенной ренты?
2. Дайте характеристику вечной ренты. Как определяются наращенная сумма и современная стоимость вечной ренты?
3. Как определяются наращенная сумма и современная стоимость ренты с выплатами в середине периода?
ТЕМА 6. ПРАКТИЧЕСКОЕ ПРИЛОЖЕНИЕ ТЕОРИИ ПРОЦЕНТНЫХ СТАВОК
В шестой теме излагаются вопросы практического приложения теории процентных ставок в финансовых расчетах. Основная цель– показать и обосновать возможности использования финансовой математики в прикладных финансовых задачах. В теме изложены следующие вопросы:
1. Изменение условий контрактов. Консолидирование задолженности на основе процентных ставок разного вида.
2. Определение доходности ссудных и учетных операций с учетом удержания комиссионных.
3. Доходность операций с ценными бумагами.
4. Доходность купли и продажи финансовых инструментов.
6.1. Изменение условий контрактов
Финансовая эквивалентность обязательств предполагает неизменность (эквивалентность) финансовых отношений сторон до и после изменения условий. Эквивалентными считаются такие платежи, которые будучи «приведенными» по заданной процентной ставке к одному моменту времени оказываются равными. Приведение разновременно выплачиваемых платежей осуществляется путем дисконтирования (приведения к более ранней дате) или, наоборот, наращения, если эта дата относится к будущему периоду.
Принцип эквивалентности обязательств лежит в основе многих финансовых расчетов долгосрочного и краткосрочного
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.