Parametric transfer functions of feedback multirate systems with disturbance acting on a continuous-time element

PARAMETRIC TRANSFER FUNCTIONS OF FEEDBACK MULTIRATE SYSTEMS WITH DISTURBANCE ACTING ON A CONTINUOUS-TIME ELEMENT

Andrej V. Panin, Vladislav O. Rybinskii

Department of Ships automation complex,

St. Petersburg State University of Ocean Technology

Lotsmanskaya st. 3, Saint-Petersberg, 190008, RUSSIA

Tel: +7(812) 7140624, E-mail: k10@smtu.ru

Abstract – The problem of constructing parametrical transfer functions (PTF) of feedback multirate sampled-data systems with disturbance acting on a continuous-time plant is considered. Using the PTF obtained in the report, it is possible to investigate  multirate sampled-data systems in continuous time for typical situations encountered in practice.

1. INTRODUCTION

Now digital controllers are widely used in control loops with continuous-time plants functioning under external disturbances. Systems with digital controllers and continuous-time plants, which contain both discrete and continuous elements, are called sampled-data systems.

Some sampled-data systems used in industry include several sampling units, which are located in different parts of the system and operate with different sampling rates. Often inequality of the sampling periods is caused by insurmountable objective factors. Investigation of such systems, called multirate sampled-data systems, is an actual research area.

Since in practice external disturbances act, as a rule, directly upon continuous-time plants, all output signals depends on continuous-time values of the inputs. Therefore, it is necessary to investigate the sampled-data systems in continuous time, taking into account their hybrid continuous-discrete structure.

One of the most perspective methods for investigation of sampled-data systems in continuous time is based on the concept of parametric transfer function (PTF) [1]. PTF is a uniform system characteristic, which makes it possible to extend many methods of classical theory of continuous-time LTI systems onto sampled-data systems [2].

Closed-form expressions are derived in [1] for PTF of multirate sampled-data systems, provided that external disturbance acts onto a sampling unit. However, the situation, when disturbance acts onto a continuous-time element, is the most typical for practice.

The aim of this report is to find closed-form expressions for PTF's of multirate sampled-data systems for the case when disturbance acts directly on a continuous-time plant.

2. STATEMENT OF A PROBLEM

Many multirate sampled-data systems encountered in applications can be approximated, with the certain degree of adequacy, by the structure shown in Fig. 1.

Here F(s), W(s), and L(s) denote transfer functions (TF) of the plant, actuator, and measuring system, respectively. It is assumed that F(s) and the product W(s) L(s) are strictly proper functions. Control signal for the actuator is generated by a digital controller C₁(s), and the measurements signal is processed by a digital controller C₂(s). The zero-order holds with TF G₀₁(s), G₀₂(s):

                                                                    (1)

are used to reconstruct continuous-time signals.

TF of the discrete controllers have the form

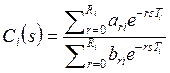
                                                                 (2)

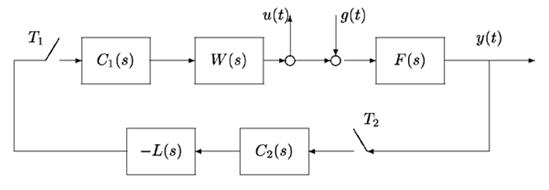
Figure 1: Multirate control system

where the integers R₁ and R₂ will be called orders of controllers; a_ri and b_ri are constants (b_0i ≠ 0), and T₁ and T₂ are the sampling periods. Hereinafter, we assume that

T₂ = NT₁,                                                                                  (3)

where N > 1 is an integer.

Let external disturbance g(t) acting on the system be applied directly to a continuous element. The output signals are stabilization error y(t) and control signal u(t).

There are two main practical problems in control system design. Analysis problem consists in estimating properties of the signals y(t) and u(t) under known disturbance g(t), provided that TF's of all elements are known as well. Solving a synthesis problem, one has to choose TF's of some elements so that characteristics of the signals y(t) and u(t) be optimal in a sense.

Denote by W_gy(s, t) the PTF of the system in Fig. 1 from input g(t) to output y(t), and by W_gu(s, t) the PTF of the system from input g(t) to output u(t). If g(t) is a centrered stochastic stationary disturbance with spectral density S_g(s), the signals y(t) and u(t) will be periodically non-stationary stochastic signals. Their variances are given by

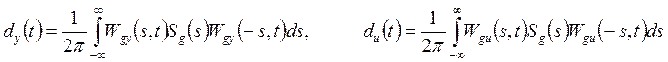                  (4)

If g(t) is a known continuous-time signal, then

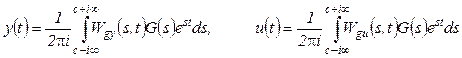                            (5)

where , and G(s) denotes the Laplace transform for g(t). All the above formulas are based on the PTF's of the system in Fig. 1 from input g(t) to outputs y(t) and u(t), and it is highly important to obtain closed-form expressions for them.

The problem considered in the report can be formulated as follows. Let us have a system with the structure shown in Fig. 1, where TF's of all continuous-time elements, and the values of the sampling periods T₁ and T₂ are known such that (3) holds. It is required to derive formulas for calculating PTF's from an input g(t) to outputs u(t) and y(t).

3. DECOMPOSITION OF PARAMETRIC TRANSFER FUNCTIONS FOR OPEN-LOOP SAMPLED-DATA SYSTEM

The algorithm of contructing PTF of multirate systems is based on a decomposition operation for discrete transfer function (DTF) [1] for open-loop sampled-data systems. Consider a realization of this operation for an open-loop system with period T₁, controller C₁(s), zero-order hold, and a continuous-time element F(s) (Fig. 2).

Assume that F(s) is strictly proper and have no multiple poles, so that

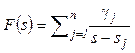                                                                               (6)

where s_j (j = 1,…,n) are poles of F(s) , while g_j (j = 1,…,n) are constants. Moreover, suppose that

                                                                        (7)

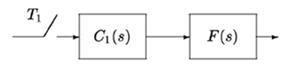
Figure 2: Open-loop sampled-data system

i.e., using the terminology of [1], the function C₁(s) is limited. Finally, we assume that C₁(s) have only simple poles.

Under these assumptions, the DTF of the open-loop system under consideration have the form [1]