Преобразование координат и эквивалентные модели. Преобразование к нормальной форме

 Санкт-Петербургский Государственный Университет

Информационных Технологий Механики и Оптики

Кафедра Систем  Управления  и Информатики

Нелинейные и оптимальные системы

Лабораторная работа № 6

"Преобразование координат  и эквивалентные модели. Преобразование к нормальной форме."

Санкт-Петербург

2008 г.

1.  Преобразование координат и эквивалентные модели.

Цель работы:проверить эквивалентность систем, полученных при заданном преобразовании координат, исследовать основные свойства эквивалентных систем.

Исследование:

1.1   Преобразование координат вида .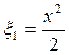

Представим преобразование в форме:

Данное отображения называется регулярным преобразованием координат, так как  преобразование φ(x) является диффеоморфизмом .

Эквивалентную модель получим в виде:

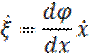
Тогда система описывается уравнением: 

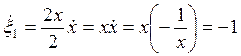
Решение для полученной системы имеет вид :

Свойство эквивалентности систем проверяется выражением:

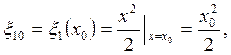
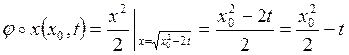- равенство выполняется, значит системы эквивалентны.

1.2   Преобразование координат вида

Проведя рассуждения аналогичные пункту 1.1, выясняем, что данное отображения является регулярным преобразованием координат.

Полученная модель будет описываться выражением:

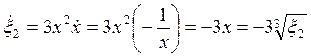
Решение имеет вид:

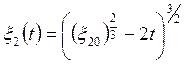
Свойство эквивалентности систем проверим выражением:

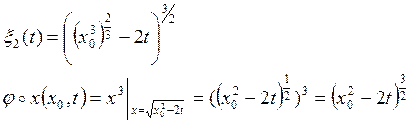
Равенство выполняется, следовательно, системы эквивалентны.

Исследуем переходные процессы эквивалентных систем и проверим их основные свойства.

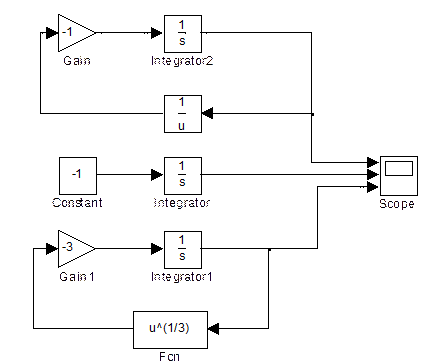
Рис.1- схема моделирования эквивалентных систем.

Переходные процессы полученных систем представлены на рисунке 2.

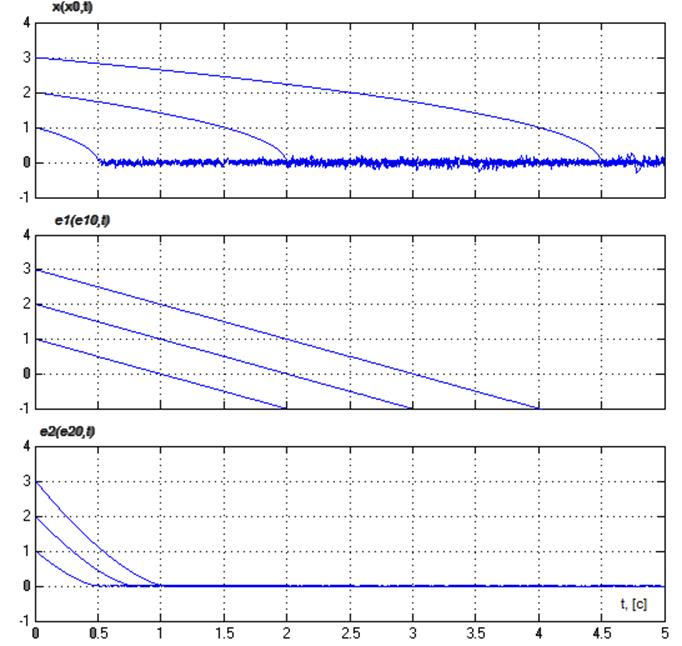
Рис.2- переходные процессы эквивалентных систем.

·   .

Система неполная, неустойчивая.

·  .

Система полная, неустойчивая.

·   .

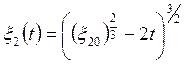Система неполная, неустойчивая.

2.  Преобразование к нормальной форме.

Цель работы: преобразовать заданные модели ОУ к нормальной форме и проанализировать устойчивость нулевой динамики эквивалентных систем.

Исследование:

Пусть нелинейная система задана в форме:

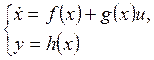
Нормальная форма системы представляется в виде:

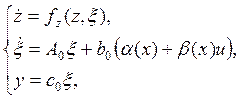
Где   ,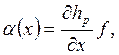    

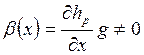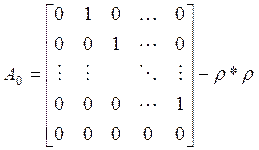
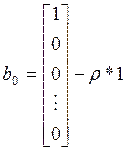
ρ- относительная степень системы.

Относительная степень системы будет определятся с помощью последовательного дифференцирования уравнения выхода.

·  ОУ1:

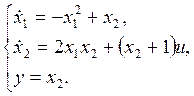
В заданной системе:

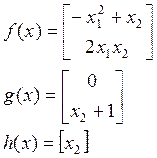
Для векторной функции

            

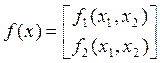
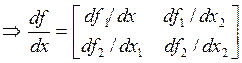
Следовательно,

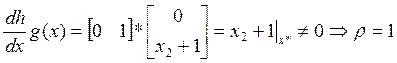
Тогда,

 

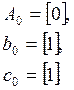
Для приведения к нормальной форме, вычислим:

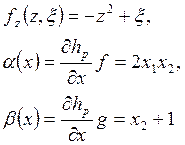
Нуль-динамика системы устойчива.

Проведем далее аналогичные рассуждения для других объектов управления.

ОУ2:

a)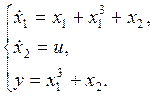 

Относительная степень системы:

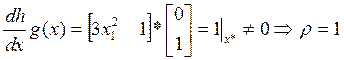
Параметры нормальной формы модели:

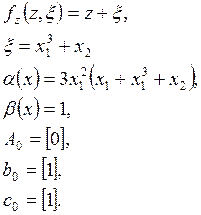
Нуль-динамика системы неустойчива.

b)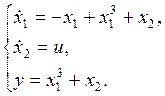 

Относительная степень системы:

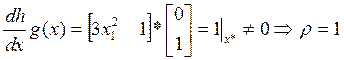
Параметры нормальной формы модели:

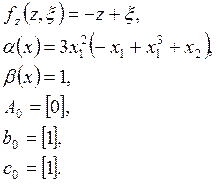
Нуль-динамика системы устойчива.

c)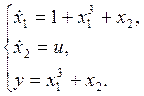 

Относительная степень системы:

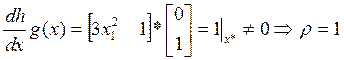
Параметры нормальной формы модели:

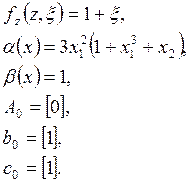
Нуль-динамика системы неустойчива.

d)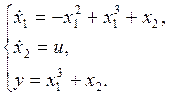 

Параметры нормальной формы модели:

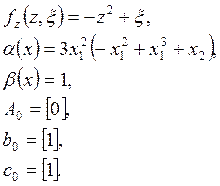
Нуль-динамика системы устойчива.

ОУ3:

a)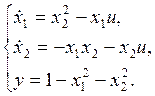 

Относительная степень системы:

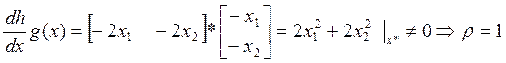
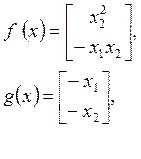
Параметры нормальной формы модели:

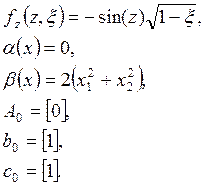
b)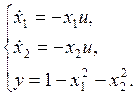 

Относительная степень системы

Параметры нормальной формы модели:

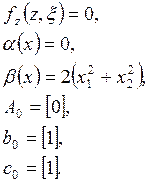
c)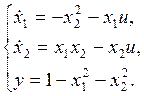 

Параметры нормальной формы модели:

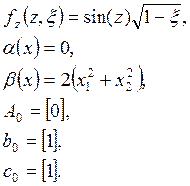
Вывод: в ходе работы получены модели эквивалентные заданной с помощью указанного преобразования координат, проверена их эквивалентность, подтверждено сходство основных свойств эквивалентных моделей. Заданные нелинейные системы приведены к нормальной форме и исследована устойчивость их нуль-динамики.