Докажем приведенные формулы, используя определение производной и доказанные теоремы.
7. ![]()
По определению производной
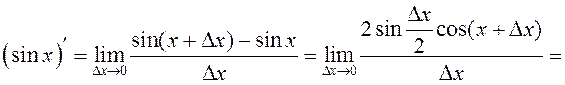
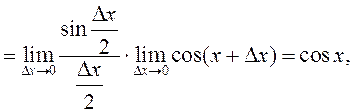
так
как 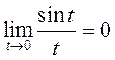 (первый замечательный предел) и функция
(первый замечательный предел) и функция ![]() непрерывна.
непрерывна.
8. ![]()
Используем формулы приведения и теорему о производной сложной функции:
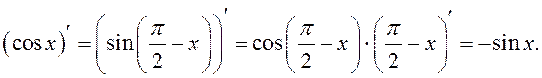
9.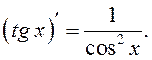
Доказать
самостоятельно, используя формулы 7, 8 и теорему о производной частного: 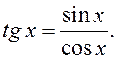
10.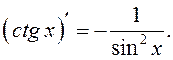
Доказать самостоятельно.
5.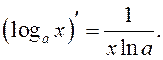
По определению
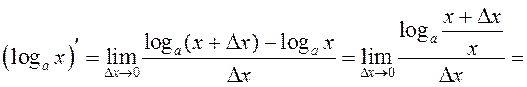
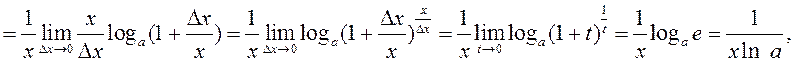
так как 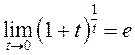 (второй замечательный
предел) и
(второй замечательный
предел) и ![]() – непрерывная функция.
– непрерывная функция.
ЗАМЕЧАНИЕ. Так
как ![]() , то
, то 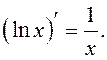
Найдем
производную функции ![]() По определению модуля
По определению модуля
 , поэтому
, поэтому 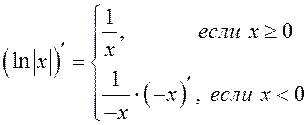 , то есть
, то есть
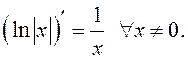
3. 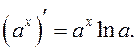
Функция
![]() – обратная для функции
– обратная для функции ![]() По теореме о производной обратной функции
По теореме о производной обратной функции
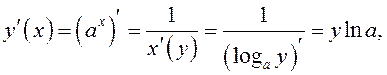
но
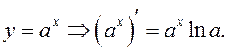
11.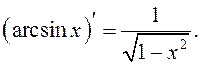
Рассмотрим
функцию 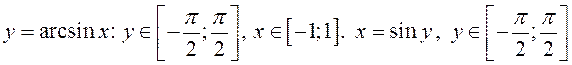 – обратная функция, поэтому по теореме о
производной обратной функции имеем:
– обратная функция, поэтому по теореме о
производной обратной функции имеем:
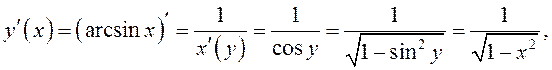
так как 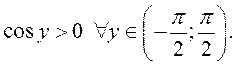
Заметим, что функция ![]() дифференцируема
во всех точках
дифференцируема
во всех точках ![]() , а
, а ![]() не
существуют.
не
существуют.
12. 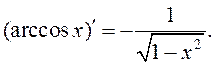
Воспользуемся известным тождеством:
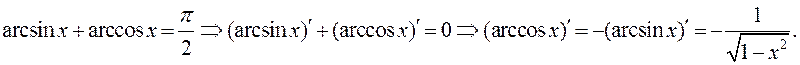
13.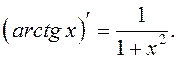
Для функции 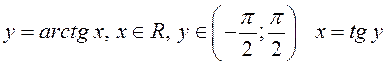 –
обратная, поэтому
–
обратная, поэтому
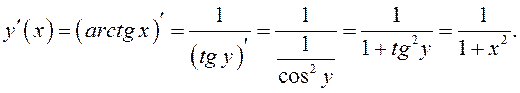
14. 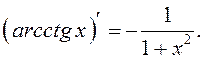
Воспользуемся тождеством:
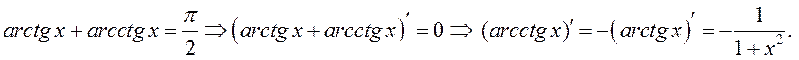
2. 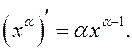
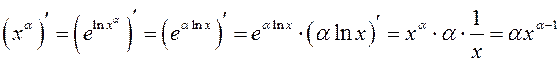 по теореме о производной
сложной функции и формулам 4 и 6.
по теореме о производной
сложной функции и формулам 4 и 6.
ПРИМЕРЫ. Найти производные функций
![]() и
и 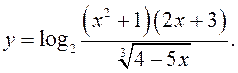
1. ![]() –
сложная функция:
–
сложная функция:
![]()
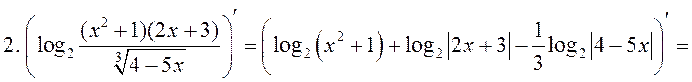
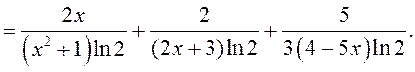
ИНВАРИАНТНОСТЬ ФОРМЫ ПЕРВОГО ДИФФЕРЕНЦИАЛА
По определению дифференциал (первый дифференциал)
функции ![]() вычисляется по формуле
вычисляется по формуле ![]() если
если ![]() –
независимая переменная.
–
независимая переменная.
ПРИМЕР. 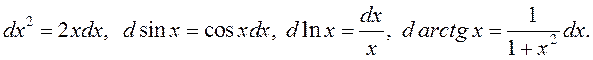
Покажем, что форма первого дифференциала остается
неизменной (является инвариантной) и в том случае, когда аргумент функции ![]() сам является функцией, то есть для сложной
функции
сам является функцией, то есть для сложной
функции ![]() .
.
Пусть
![]() дифференцируемы, тогда по определению
дифференцируемы, тогда по определению
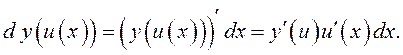
Кроме
того, ![]() что и требовалось доказать.
что и требовалось доказать.
ПРИМЕРЫ.
![]()
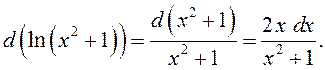
Доказанная инвариантность
формы первого дифференциала позволяет считать, что 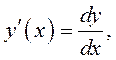 то
есть производная равна отношению дифференциала функции к дифференциалу
ее аргумента, независимо от того, является ли аргумент независимой
переменной или функцией.
то
есть производная равна отношению дифференциала функции к дифференциалу
ее аргумента, независимо от того, является ли аргумент независимой
переменной или функцией.
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ,
ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ
Пусть ![]() Если функция
Если функция ![]() имеет на множестве
имеет на множестве ![]() обратную, то
обратную, то ![]() Тогда
равенства
Тогда
равенства 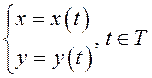 определяют на множестве
определяют на множестве ![]() функцию, заданную параметрически,
функцию, заданную параметрически, ![]() –параметр (промежуточная
переменная).
–параметр (промежуточная
переменная).
ПРИМЕР. Построить график функции 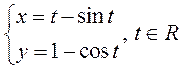 .
.
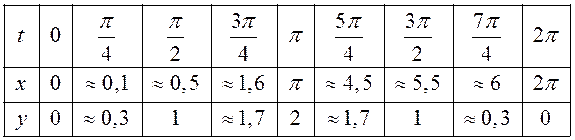
|
1 О
1 Рис. 25 |
Построенная кривая называется циклоидой (рис. 25) и является траекторией точки на окружности радиуса 1, которая катится без скольжения вдоль оси ОХ.
ЗАМЕЧАНИЕ. Иногда, но не всегда, из параметрических уравнений кривой можно исключить параметр.
ПРИМЕРЫ. 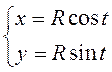 – параметрические уравнения окружности,
так как, очевидно,
– параметрические уравнения окружности,
так как, очевидно, ![]()
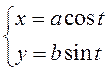 – параметрические
уравнения эллипса, так как
– параметрические
уравнения эллипса, так как 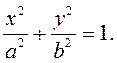
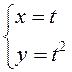 – параметрические
уравнения параболы
– параметрические
уравнения параболы ![]()
Найдем производную функции, заданной параметрически:
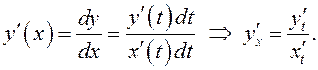
Производная функции, заданной параметрически, – также
функция, заданная параметрически: 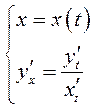 .
.
ОПРЕДЕЛЕНИЕ. Второй производной функции называется производная от ее первой производной.
Производной ![]() -го порядка называется
производная от ее производной порядка
-го порядка называется
производная от ее производной порядка ![]() .
.
Обозначают производные второго и ![]() -го порядка так:
-го порядка так:
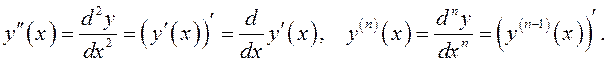
Из
определения второй производной и правила дифференцирования параметрически
заданной функции следует, что 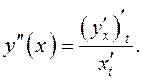 Для вычисления третьей
производной надо представить вторую производную в виде
Для вычисления третьей
производной надо представить вторую производную в виде 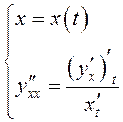 и
воспользоваться еще раз полученным правилом. Производные старших порядков
вычисляются аналогично.
и
воспользоваться еще раз полученным правилом. Производные старших порядков
вычисляются аналогично.
ПРИМЕР. Найти производные первого и второго порядков функции
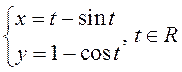 .
.
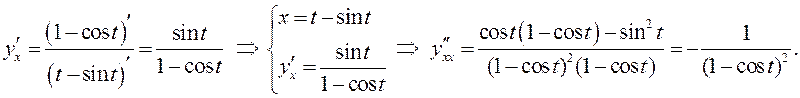
ОСНОВНЫЕ ТЕОРЕМЫ
ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
ТЕОРЕМА
(Ферма). Пусть функция ![]() имеет в точке
имеет в точке ![]() экстремум. Если существует
экстремум. Если существует ![]() , то
, то ![]()
ДОКАЗАТЕЛЬСТВО.
Пусть ![]() , например, – точка минимума. По
определению точки минимума существует окрестность этой точки
, например, – точка минимума. По
определению точки минимума существует окрестность этой точки ![]() , в пределах которой
, в пределах которой ![]() , то есть
, то есть ![]() – приращение
– приращение
![]() в точке
в точке ![]() . По
определению
. По
определению 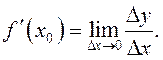 Вычислим односторонние производные
в точке
Вычислим односторонние производные
в точке ![]() :
:
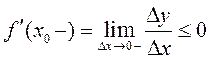 по
теореме о предельном переходе в неравенстве, так как
по
теореме о предельном переходе в неравенстве, так как ![]()
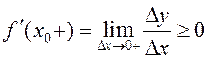 , так как
, так как ![]() Но по условию
Но по условию ![]() существует,
поэтому левая производная равна правой, а это возможно лишь если
существует,
поэтому левая производная равна правой, а это возможно лишь если ![]()
Предположение о том, что ![]() – точка
максимума, приводит к тому же.
– точка
максимума, приводит к тому же.
Геометрический смысл теоремы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.