Линейная алгебра. Векторная алгебра. Аналитическая геометрия: Конспект лекций, страница 3

ОПРЕДЕЛЕНИЕ.  Пусть = – матрица размера , = – матрица размера . Произведение этих матриц   – матрица  = размера , элементы которой вычисляются по формуле:

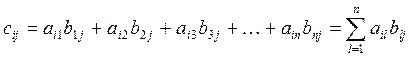,    =1,2,…,,    =1,2,…,, то есть элемент -й строки  и -го столбца матрицы  равен сумме произведений соответствующих элементов -й строки матрицы  и -го столбца матрицы  .

ПРИМЕР.

=  , = 

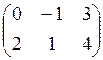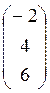
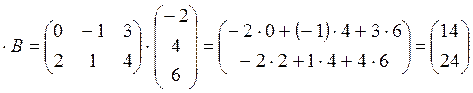
2х3                3х1                       2х3         3х1                  2х1

Произведение 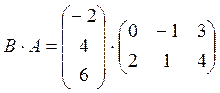 – не существует.

3х1        2х3

CВОЙСТВА ОПЕРАЦИИ УМНОЖЕНИЯ МАТРИЦ

1. , даже если оба произведения определены.

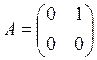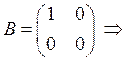
ПРИМЕР.   ,  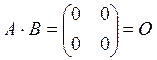   , хотя

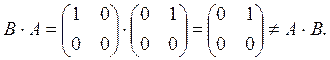
ОПРЕДЕЛЕНИЕ. Матрицы  и  называются перестановочными, если , в противном случае  и  называются неперестановочными.

Из определения следует, что перестановочными могут быть лишь квадратные матрицы одного размера.

ПРИМЕР.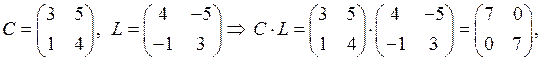 

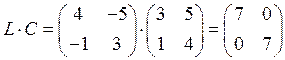
 матрицы  и   перестановочные.

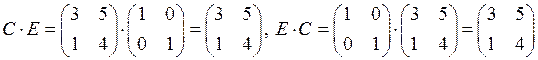, то есть , значит,   и  – перестановочные матрицы.

Вообще единичная матрица перестановочна с любой квадратной матрицей того же порядка, и для любой матрицы . Это свойство матрицы  объясняет, почему именно она называется единичной: при умножении чисел таким свойством обладает число 1.

Если соответствующие  произведения определены, то:

2.             

3. , 

4.              

5.

ПРИМЕР.

,        

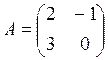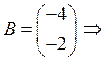
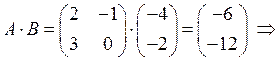
2х2      2х1     2х1                          1х2

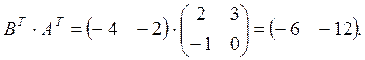
1х2         2х2           1х2

ЗАМЕЧАНИЕ. Элементами матрицы могут быть не только числа, но и функции. Такая матрица называется функциональной.

ПРИМЕР.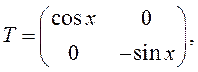       

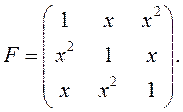
ОПРЕДЕЛИТЕЛИ  И  ИХ  СВОЙСТВА

Каждой квадратной матрице можно по определенным правилам поставить в соответствие некоторое число, которое называется ее определителем.

Рассмотрим  квадратную  матрицу  второго  порядка: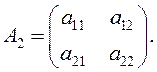   

Её определителем называется число, которое записывается и вычисляется так:

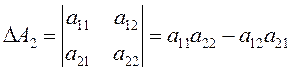                                      (1.1)

Такой определитель называется определителем второго порядка и может обозначаться по-другому: 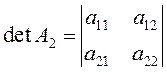  или .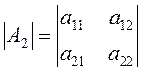

Определителем третьего порядка называется число, соответствующее квадратной матрице 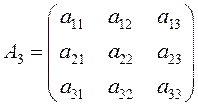 , которое вычисляется по правилу:

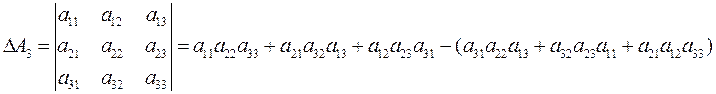   (1.2)

Это правило вычисления определителя третьего порядка называется правилом треугольников и схематически его можно представить так:

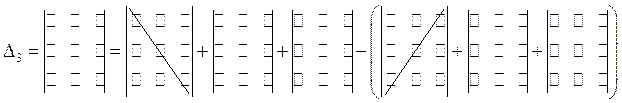
ПРИМЕР. ;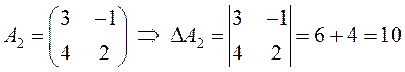   

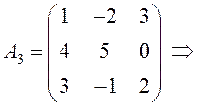
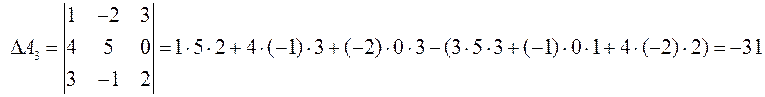
Если справа от определителя приписать первый, а затем второй столбец, то правило треугольников можно модифицировать:

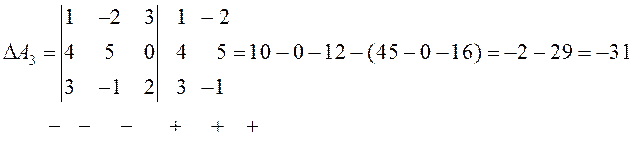
Сначала умножаются числа на главной диагонали и двух ей параллельных диагоналях, затем – числа на другой (побочной) диагонали и ей параллельных. Из суммы первых трех произведений вычитается сумма остальных.

Группируя слагаемые в (1.2) и используя (1.1), заметим, что

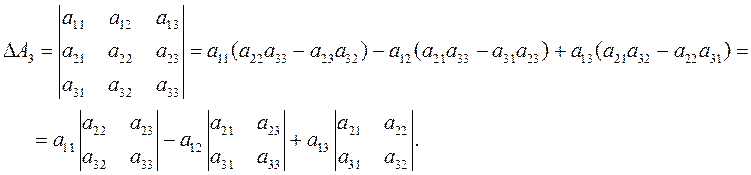 (1.3)

То есть при вычислении определителя третьего порядка используются определители второго порядка, причем 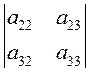  – определитель матрицы, полученный из  вычеркиванием элемента  (точнее, первой строки и первого столбца, на пересечении которых стоит ),  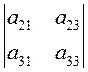 – вычеркиванием 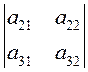элемента ,  – элемента .

ОПРЕДЕЛЕНИЕ. Дополнительным минором  элемента  квадратной матрицы  называется определитель матрицы, получаемой из  вычеркиванием -ой строки и -го столбца.

ПРИМЕР.

 

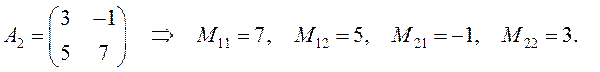
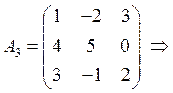
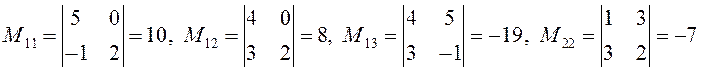
и так далее:  матрица третьего порядка  имеет  9 дополнительных миноров.

ОПРЕДЕЛЕНИЕ. Алгебраическим  дополнением элемента  квадратной матрицы  называется  число .

ПРИМЕР.

Для матрицы : 

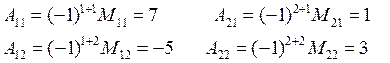
Для матрицы :  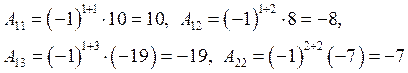  и так далее.

Итак, с учетом сформулированных определений (1.3) можно переписать в виде:   .

Перейдем теперь к общему случаю.

ОПРЕДЕЛЕНИЕ. Определителем квадратной матрицы  порядка  называется число, которое записывается и вычисляется следующим образом:

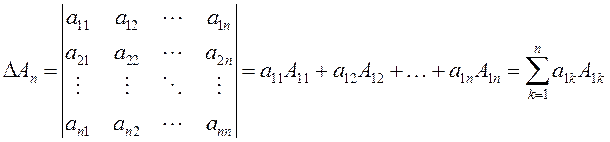                      (1.4)

Равенство (1.4) называется разложением определителя по элементам первой строки. В этой формуле алгебраические дополнения вычисляются как определители -го порядка. Таким образом, при вычислении определителя  4-го порядка по формуле (1.4) надо, вообще говоря, вычислить 4 определителя 3-го порядка; при вычислении определителя 5-го порядка – 5 определителей   4-го порядка и т.д. Однако если, к примеру, в определителе 4-го порядка первая строка содержит 3 нулевых элемента, то в формуле (1.4) останется лишь одно ненулевое слагаемое.