ОПРЕДЕЛЕНИЕ.
Коэффициенты, определенные по формулам (13.30), (13.34) и (13.35), называются коэффициентами
Фурье функции ![]() , а тригонометрический ряд
(13.27) с такими коэффициентами называется тригонометрическим рядом Фурье
функции
, а тригонометрический ряд
(13.27) с такими коэффициентами называется тригонометрическим рядом Фурье
функции ![]() .
.
ЗАМЕЧАНИЕ.
Название «тригонометрический» некоторого функционального ряда означает, что
этот ряд имеет вполне определенный вид: его членами являются тригонометрические
функции вида ![]() и
и ![]() с теми
или иными коэффициентами. Название же «ряд Фурье» указывает на вполне определенное
происхождение его коэффициентов: формулы (13.30), (13.34) и (13.35).
с теми
или иными коэффициентами. Название же «ряд Фурье» указывает на вполне определенное
происхождение его коэффициентов: формулы (13.30), (13.34) и (13.35).
Переход от
отрезка ![]() к любому другому не является принципиальным
и, как будет показано позже, может быть легко осуществлен.
к любому другому не является принципиальным
и, как будет показано позже, может быть легко осуществлен.
Теперь так
же, как и при изучении ряда Тейлора, поставим вопрос: какими свойствами должна
обладать функция ![]() , чтобы составленный для нее ряд
Фурье сходился, причем именно к той функции, для которой он составлен?
, чтобы составленный для нее ряд
Фурье сходился, причем именно к той функции, для которой он составлен?
Ответ на этот вопрос содержится в теореме Дирихле.
ОПРЕДЕЛЕНИЕ.
Функция ![]() называется кусочно-монотонной на
отрезке
называется кусочно-монотонной на
отрезке ![]() , если этот отрезок можно разбить на
конечное число частей так, что на каждой из них функция монотонна, то есть либо
убывает, либо возрастает, либо постоянна.
, если этот отрезок можно разбить на
конечное число частей так, что на каждой из них функция монотонна, то есть либо
убывает, либо возрастает, либо постоянна.
ОПРЕДЕЛЕНИЕ.
Функция ![]() называется кусочно-непрерывной на
отрезке
называется кусочно-непрерывной на
отрезке ![]() , если она имеет на этом отрезке конечное
число точек разрыва первого рода.
, если она имеет на этом отрезке конечное
число точек разрыва первого рода.
ОПРЕДЕЛЕНИЕ.
Функция ![]() удовлетворяет условиям Дирихле на
отрезке
удовлетворяет условиям Дирихле на
отрезке ![]() , если она на этом отрезке кусочно-монотонна
и кусочно-непрерывна.
, если она на этом отрезке кусочно-монотонна
и кусочно-непрерывна.
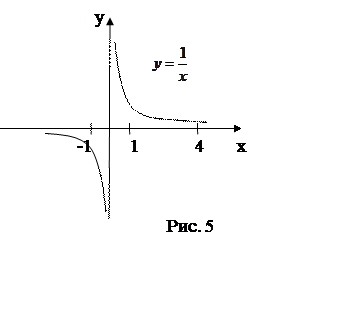 ПРИМЕР. а) Функция
ПРИМЕР. а) Функция 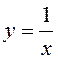 удовлетворяет условиям Дирихле на отрезке
удовлетворяет условиям Дирихле на отрезке ![]() и не удовлетворяет этим условиям на
и не удовлетворяет этим условиям на ![]() : в точке
: в точке ![]() она
имеет разрыв второго рода (рис. 5).
она
имеет разрыв второго рода (рис. 5).
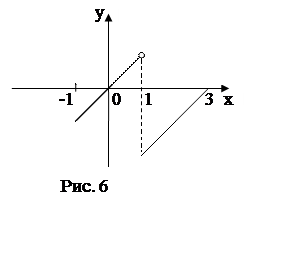 б) Функция
б) Функция 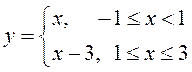 (рис.
6) удовлетворяет условиям Дирихле на отрезке
(рис.
6) удовлетворяет условиям Дирихле на отрезке
![]() . в) Функция
. в) Функция 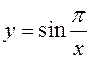 на отрезке
на отрезке ![]() имеет
бесконечное множество интервалов монотонности, так как монотонна на отрезках
имеет
бесконечное множество интервалов монотонности, так как монотонна на отрезках 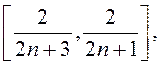
![]() . Из
этого следует, что она не является кусочно-монотонной на
. Из
этого следует, что она не является кусочно-монотонной на ![]() . Кроме того, точка
. Кроме того, точка ![]() – точка разрыва второго рода:
– точка разрыва второго рода: 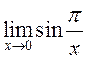 не существует (см.гл.4). Значит, эта
функция не удовлетворяет условиям Дирихле на отрезке
не существует (см.гл.4). Значит, эта
функция не удовлетворяет условиям Дирихле на отрезке ![]() .
На любом отрезке, не содержащем точку
.
На любом отрезке, не содержащем точку ![]() ,
условия Дирихле для этой функции выполнены.
,
условия Дирихле для этой функции выполнены.
ТЕОРЕМА
Дирихле (достаточное условие разложимости функции в
ряд Фурье). Пусть ![]() -периодическая функция
-периодическая функция ![]() удовлетворяет на отрезке
удовлетворяет на отрезке ![]() условиям Дирихле. Тогда составленный для
нее тригонометрический ряд Фурье сходится
условиям Дирихле. Тогда составленный для
нее тригонометрический ряд Фурье сходится ![]() . При
этом, если
. При
этом, если ![]() – точка непрерывности
– точка непрерывности ![]() , то его сумма
, то его сумма ![]() ; если
же
; если
же ![]() – точка разрыва первого рода, то сумма
ряда
– точка разрыва первого рода, то сумма
ряда 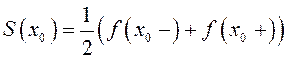 , где
, где ![]() и
и ![]() – левый и правый пределы
– левый и правый пределы ![]() в этой точке.
в этой точке.
Без доказательства.
ПРИМЕР.
Разложить в ряд Фурье функцию 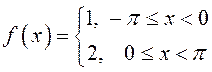 .
.
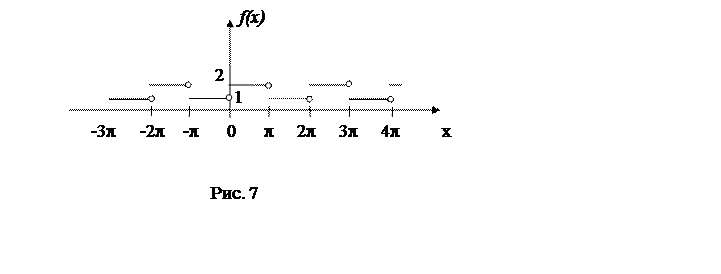
Такая постановка
задачи означает, что задан один период ![]() -периодической
функции (рис.7), которую нужно разложить в ряд Фурье.
-периодической
функции (рис.7), которую нужно разложить в ряд Фурье.
 |
Найдем коэффициенты ряда по формулам (13.30), (13.34) и (13.35).
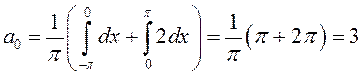 ;
;
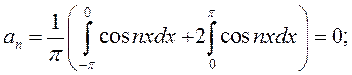
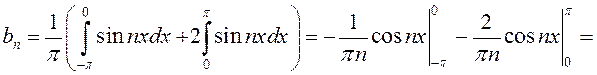
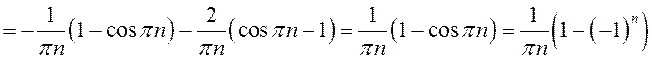 .
.
Следовательно, в соответствии с (13.28)
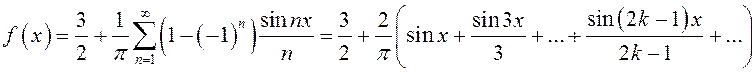 .
.
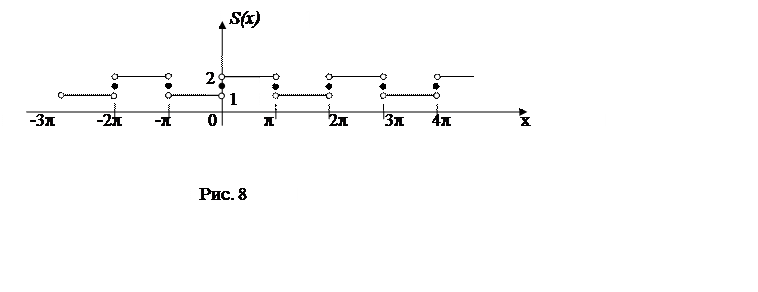
По теореме
Дирихле сумма этого ряда в точках разрыва отличается от значений функции в этих
точках, в остальных точках они совпадают. Например, 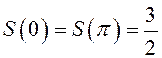 ,
, ![]() . График суммы ряда представлен на
рис.8.
. График суммы ряда представлен на
рис.8.
 |
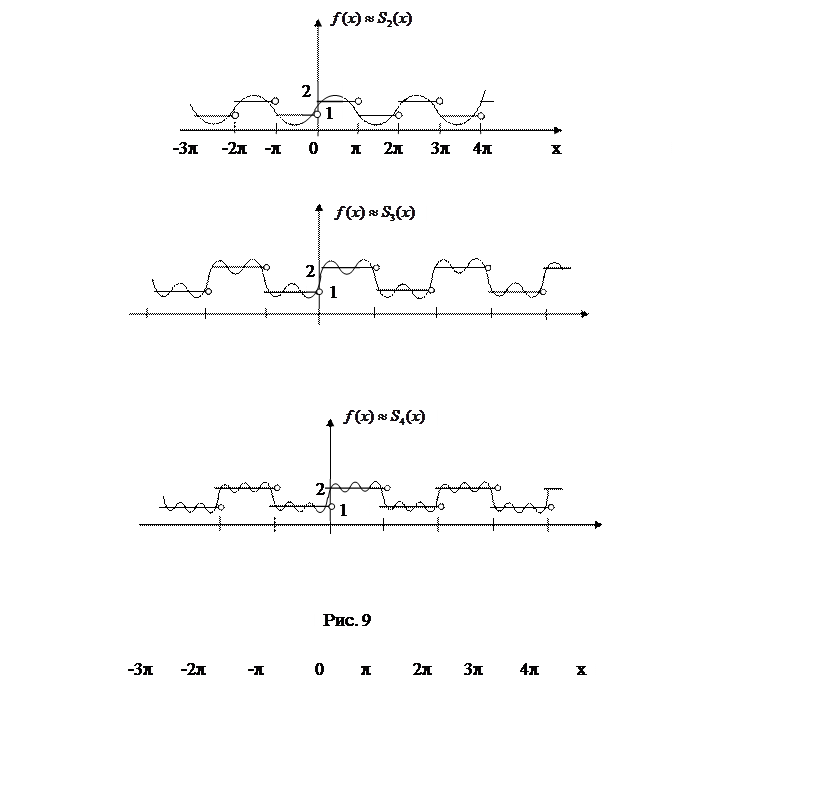
По определению
сходимости ряда его частичные суммы приближают сумму с различной точностью: чем
больше номер ![]() частичной суммы, тем точнее приближение
частичной суммы, тем точнее приближение ![]() . На рис. 9 показан характер приближения
данной функции
. На рис. 9 показан характер приближения
данной функции ![]() частичными суммами построенного
ряда Фурье.
частичными суммами построенного
ряда Фурье.
 |
|
ЗАМЕЧАНИЕ.
Полученный ряд сходится по теореме Дирихле ![]() ,
например, в точке
,
например, в точке ![]() . Сумма ряда в этой точке равна
. Сумма ряда в этой точке равна ![]() , то есть
, то есть 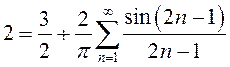 .
Отсюда следует, что знакопеременный ряд
.
Отсюда следует, что знакопеременный ряд 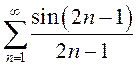 сходится.
сходится.
Заметим, что признаки сходимости рядов, изученные в п.13.1, не позволяли исследовать поведение такого ряда. Кроме того, легко находится и его сумма:
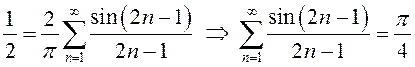 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.