Изучение методов помехоустойчивого кодирования и декодирования информации с помощью циклических блочных кодов Боуза-Чоудхури-Хоквингвема

2.1. Задание циклического кода с помощью элементов конечного поля

Корректирующий циклический (n, k) код С представляется в виде вектора-строки  или в полиномиальном виде как

, где  - кольцо многочленов над полем .

Обозначим  примитивный элемент конечного поля как α. Определим проверочную матрицу кода , столбцы которой равны , где . Произведению (^T) соответствует полином синдрома

.

Для дальнейшего изложения полезно ввести следующие понятия.

Минимальный многочлен. Пусть - поле,  - подполе поля  и α – элемент мультипликативной группы  - {0} поля . Обозначим через  множество всех многочленов над , корнем которых является α. Пусть  - нормированный многочлен минимальной степени в ; этот многочлен называется минимальным многочленом элемента α над . Минимальный многочлен является неприводимым.

Пример. Рассмотрим поле , . Возможными коэффициентами для минимального многочлена являются 0 или 1. Получаем следующее соответствие (табл.1)

Таблица1

Сопряженные элементы и циклотомические классы. Минимальные многочлены элементов  и  равны. Элементы поля, минимальные многочлены которых равны, называются сопряженными. Так для поля  мнимальным многочленом элементов  (при этом ) является один и тот же многочлен. Аналогично для  минимальным многочленом является один и тот же многочлен. Видно, что степени элемента  распадаются на непересекающие множества, которые называются циклотомическими классами. Когда индекс j пробегает циклотомический класс, то минимальным для всех  является один и тот же многочлен.

Множество целых чисел по модулю  относительно операции умножения на p распадается на подмножества, которые называются циклотомическими классами по модулю . Циклотомический класс, содержащий s, состоит из чисел

, где - наименьшее положительное целое число, такое, что .

Например, циклотомическими классами по модулю 15 (для p= 2) являются K₀ = ={0}; K₁ = {1,2,4,8}; K₃ = {3,6,12,9}; K₅ = {5,10}; K₇ = {7,14,13,11}.

Циклотомические классы позволяют вычислить минимальные полиномы с помощью выражения 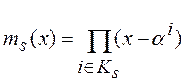. Используя введенные определения, можно построить следующую конструкцию (n, k) кода.

1.  Представим кодируемую информацию (сообщение) a(x) старшей частью полинома

.

2.  Найдем остаток Rem(x) от деления сообщения a(x) на минимальный полином :                                            .

3.  Сформируем кодовое слово по правилу

.

Декодирование принимаемого сигнала можно вести в следующей последовательности. Подставим  в  и вычислим синдром ошибки S=y(a). Тогда если , то ошибок в принятом сигнале нет; если , то  для некоторого j. Полином ошибки . Следовательно, принимаемый символ  ошибочен и должен быть исправлен

Пример. Пусть двоичное сообщение имеет вид a = (1,1,0,1,1,0,1,0,0,0,0). Применим код (15,11). Образуем полином .

Разделим сообщение a(x) на минимальный полином , : , .

Кодовое слово равно .

Пусть вектор принимаемого сигнала равен  и . Если a - корень m(x), то, используя правила сложения в поле GF(2⁴), получим

.

Следовательно, ошибка произошла на позиции j= 2. Полином ошибки . Символ y₂ должен быть исправлен с1 на 0.

Рассмотрим случай, когда требуется корректировать две ошибки. Минимальный полином m₁(x) элемента a будет иметь своими корнями также все элементы a^j, jÎK₁. Использование полинома m₁(x) достаточно для коррекции одной ошибки, но недостаточно для исправления двух ошибок. Обратимся к коду Хэмминга (15,11), p^k = =16, K₁={1,2,4,8}. Возьмем элемент поля , которому соответствует минимальный неприводимый в  полином . Элемент a³ является корнем полинома (x⁵-1). Элементы a и a³ являются корнями полинома

Если полином сообщения a(x) разделить на m₁₃(x), то для кода с n = 15 получим остаток Rem(x) степени не выше 7:

,  .

В этом случае сообщение длиной 7 может быть закодировано кодовым словом, , состоящим из 15 символов.

Процесс декодирования подобен процедуре исправления одной ошибки, но при исправлении двух ошибок требуется решить квадратное уравнение. Запишем принимаемый сигнал в виде , где y(x) – полином ошибок.

Для рассматриваемого примера . Ошибки в принимаемом сигнале отсутствуют в том случае, если  или . Если произошла одна ошибка, то  для различных значений e. В этом случае  и . Если в принимаемом сигнале два символа ошибочны, то  для различных значений e, f, e¹f, при этом  и .

Определим уравнение , которое имеет два корня  и , при этом , . Заметим, что корни уравнения однозначно связаны с координатами eи fошибок. Решение уравнения позволяет определить местоположение ошибок в декодируемом сигнале. Многочлен в левой части уравнения может быть найден с использованием синдромов ошибок следующим образом. Компоненты S_i вектора синдромов  и коэффициенты полинома позиций ошибок связаны соотношениями

; ; .

По рассмотренным примерам можно сделать обобщение и дать определение кодов Боуза–Чоудхури–Хоквингвема (БЧХ).

2.2. БЧХ-коды

Определение примитивного БЧХ-кода. Пусть  - целые числа, тогда q-ичный БЧХ-код имеет параметры . Код формируется генераторным полиномом , имеющим корнями примитивный элемент поля , ,. Соответственно

                           ,                                       (1)

где  - минимальный полином, соответствующий элементу поля .

Для  в поле  элементы  и  имеют одинаковые минимальные полиномы, поэтому для двоичного БЧХ-кода: