Динамическая игра преследования с «линией жизни» с участием космических аппаратов с двигателями малой тяги - солнечными парусами, страница 2

Назовем пару f_p = (x , S_p)  (f_E = (y , S_E)) , где х (у) – орбиты игрока Р (Е), а S_p (S_E) – активная площадь СП, позицией игрока Р (Е). Множество позиций, достижимых игроком Р (Е) из позиции f_p = (x , S_p)  (f_E = (y , S_E)) за один импульс обозначим через. Множество позиций игрока Р (Е) обозначим через F_p, F_E.

Множество позиций достижимых игроком Р (Е) из позиции f_p = (x , S_p)  (f_E = (y , S_E)) при любом возможном числе импульсов обозначим через

Позиция игры есть пара f = (f_p, f_E), их множество обозначим через F = F_p ^x F_E. Обозначим радиус и полярный угол КА через r и θ, величину импульса через V, угол наклона импульса к местному горизонту (угол установки паруса) через γ. Тогда переход из фиксированной позиции к следующей определяется на основе следующего соотношения [3] :

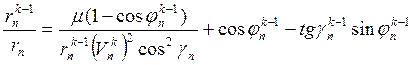   (1)

Отсюда при n = 1 получаем алгоритм перехода игрока Р из (k-1) –ой позиции в k – ую позицию, при n = 2 получаем алгоритм перехода игрока Е из (k-1) –ой позиции в k – ую позицию. В (1) - угловая дальность, μ – гравитационный параметр центрального тела.

На пространстве позиции игры  введем функцию расстояния следующим образом:

                                (2)

 - положения КА Р и Е соответственно, на орбите в момент времени t. Здесь мы считаем, для простоты, что существует общий период Т у КА Р и Е.

Если это не имеет места, то мы будем считать, что на множестве F определена некоторая функция К(f_р, f_E) = К(f) – выигрыш игрока Р.

III. [8]  Введем новые обозначения. Зоной достижимости игрока Р (Е) будем называть множество W_p(, S_p, t)   (W_E(, S_E, t)) точек  в которые может попасть Р (Е) в момент t, используя все возможные допустимые управления – выбор угла установки паруса. Будем считать W_p(, S_p, t)   (W_E(, S_E, t)) ограниченным множеством с границей д W_p(, S_p, t)  (д W_E( , S_E, t)).

Обозначим через W_p^l(, S_p, t) , l – окрестность W_p(, S_p, t).

Зоной безопасности игрока Е (ЗБЕ) назовем множество точек , каждую из которых Е может достигнуть раньше, чем она попадет в l - окрестность положения игрока Р, при любом допустимом управлении последнего (  тогда границей дН ЗБЕ будет множество точек, лежащих на пересечении д W_p^l(, S_p, t) ∩ д W_E(, S_E, t) , и удовлетворяющих условию t_E=t_{p ,} . (l- радиус действия поражения Р)

Игрок Р преследует Е, который убегая, стремится достигнуть δ – окрестность δА, до того как будет пойман игроком Р. Преследователь минимизирует, а убегающий максимизирует , и кроме того Е минимизирует . Окончанием игры считается выполнение хотя бы одного из условий :

(3)    , (4)

Ситуация (3) соответствует выигрышу Р, ситуация (4) соответствует выигрышу Е, при одновременном наступлении (3) и (4) получаем ничью, .

Т.о. имеем задачу качества для игрока Р

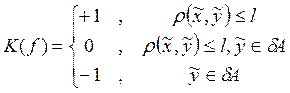                   , для игрока Е она обратна.

Для решения такой игры, получаем аналитический вид границы ЗБЕ согласно методу приведенному в [8]. Следуя данному методу получаем границы зон достижимости игроков , отсюда согласно определению получаем аналитический вид границы ЗБЕ

Теорема

Для окончания игры в пользу Е необходимо и достаточно чтобы выполнялось   (5) (граница ЗБЕ пересекается с «линией жизни» h(r)=0)

Доказательство приведено в  [8].

Неравенство (5) является решением задачи качества. Но оно может быть существенно использовано и при рассмотрении игры степени. Так при его выполнении оптимальная траектория Е находится в классе траекторий, проходящих через и принадлежащих Н. Выполнение равенства  в задаче быстродействия, говорит о том, что ее можно решать без учета ограничений на координаты Е  () как обычную игру убегания  - преследования без линии жизни, которую в свою очередь можно решать геометрическим методом изложенным в [1] , при этом роль окружности Апполония должна выполнять граница ЗБЕ.

IV.  Если игроку Р необходимо минимизировать время сближения, введем множество , т.е. множество состояний в которых гарантирован выигрыш Р.  Введем t_n- первый момент, когда игроки Р и Е попадают в это множество. . Выигрыш К(f) = t_n(f). Стратегия φ_р (φ_Е) игрока Р (Е) в игре Г(^.) есть правило, ставящее в соответствие состоянию игры  угол установки СП, а соответственно вектор импульса. Множество всех стратегий Р (Е) обозначим через Ф_р (Ф_Е).

В такой постановке игры цель Р – минимизировать К(f), а цель Е – оттянуть момент встречи. Функция  выигрыша

K(f) = 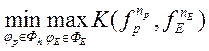.  - конечная позиция ситуации выбора пары стратегий (φ_р, φ_Е). Решается методом динамического программирования – начиная с начального состояния и последовательно доходя до конечного состояния. (подробнее можно рассмотреть на примере приведенном в [7]).

Теорема

В игре Г(^.) существуют ситуации равновесия в чистых стратегиях.

Доказательство проводится аналогично доказательству теоремы Цермело – для конечных позиционных игр с полной информацией [5-6].

Получив значение K(f) на последнем шаге, с помощью построенной функции K(f) и выбранных нами углов установки СП  последовательно вычисляются значения оптимальных управлений игроков.

Литература

1.  Айзекс Р. Дифференциальные игры. –М.,  «Мир», 1967.

2. Алексеев К.Б., Бебенин Г.Г., Ярошевский В.А. Маневрирование космических аппаратов.–М., Машиностроение, 1970.  416 с.

3. Охоцимский Д.Е.  Динамика космических полетов. –М. : Изд-во Моск. ун-та, 1968. 158с.

4. Петросян Л.А., Томский Г.В. Динамические игры и их приложения. –Л.: Изд-во Ленингр. ун-та, 1982. 252 с.

5. Балк М.Б. Элементы динамики космического полета. –М., «Наука», 1965. 340 с.

6. Малафеев О.А. Ситуация равновесия в динамических играх. – Кибернетика. 1974. №3. С. 111-118.

7. Барсегян В. Р., Малафеев О.А. Об игровых задачах в центральном Ньютоновском поле тяготения. –Я.: Изд-во Якутск. ун-та, 1988.  51-56 с.

8. Яковлев В.И. Об игре « с линией жизни» в многосвязной области. –Известия ВУЗ-ов., Математика № 4 (155) , 1975. 88-91 с.