Решение систем линейных алгебраических уравнений. Метод исключения Жордана и его модификация

Санкт-Петербургский Государственный Университет

Факультет Прикладной Математики – Процессов Управления

Курсовая работа по методам вычислений

Тема 1. Решение систем линейных алгебраических уравнений

Вариант № 20

Выполнил: студентка     

II курса 261 группы          

Мартынова А.М.

Проверил: преп.

Григорьева К.В.

Оценка:         

Санкт-Петербург

2005 г.

Оглавление:

1. Постановка задачи. 3

2. Теоретический вопрос. 4

3. Описание метода. 6

4. Текст программы.. 9

5. Результаты вычислений. 11

6. Список литературы.. 12

1. Постановка задачи

1.  Как влияют на решение систем линейных алгебраических уравнений

                             Ax = C                                            (1)

с квадратной не вырожденной матрицей А погрешности задания этой матрицы и вектора С, а так же погрешности арифметических операций, возникающих при реализации какого-нибудь точного метода решение система (1) на ЭВМ?

2.  Подробно описать метод исключении Жордана и его модификации (с выбором главного элемента по столбцу, по строке, по всей матрице) для системы (1). Сравнить его по трудоёмкости (т.е. по числу арифметических операций) с методом Гауса.

3.  Составить и отладить программу, реализующую метод Жордана (с выбором главного элемента по строке). Продемонстрировать её работу на примере системы (1) с

;                        

2. Теоретический вопрос

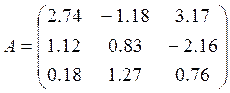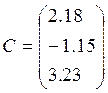
Погрешность решения задачи обуславливается следующими причинами :

- математическое описание задачи является неточным, в частности неточно заданы исходные данные описания (матрицы А и С)

- применяемый для решения метод не является точным: получение точного решения возникающей математической задачи требует неограниченного или неприемлемо большого числа арифметических операций, поэтому вместо точного решения задачи приходится прибегать к приближенному

- при вводе данных на ЭВМ, при выполнении арифметических операций и при выводе данных производятся округления.

Погрешность, соответствующая этим причинам, называют неустранимой, т. е. погрешность являющуюся следствием неточности задания числовых данных, входящих в математическое описание задачи, что и наблюдается в нашем случае.

Пусть решается линейная система Ax = c, A  М_n, c  Сⁿ . Пусть В - алгоритм решения этой системы на идеальной вычислительной системе, так, что x = B(A, c) - точное решение системы и потому x = B(A, c) - отображение на классе невырожденных матриц (x = A^-1b). Пусть В - тот же алгоритм, реализованный на реальной вычислительной системе. В результате его проведения получено приближенное решение x’ = В(A, c) . Определим матрицу A’ и вектор c’ из условия x’ = В(A’, c’)   (c’ = A’^-1x’), т.е. x’ является точным решением системы A’x’ = c’.  Обозначим A’ = A + E, c’ = c + e . Таким образом, точное решение x удовлетворяет системе Ax = c , а приближенное решение x удовлетворяет системе (A + E)x’ = c + e .

Пусть - произвольная матричная норма, согласованная с векторной нормой . Будем считать, что ошибка, вносимая в матрицу при проведении алгоритма, не очень велика: 

 

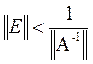
Отсюда следует, что матрица A + E обратима. Вычислим погрешность x – x’ :

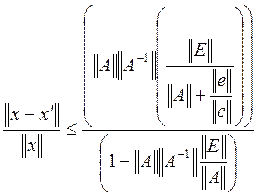
Определение.   Числом обусловленности матрицы A по отношению к матричной норме называется

 , если А невырождена.

 , если А вырождена.

С использованием этого обозначения последнее неравенство можно переписать в виде:

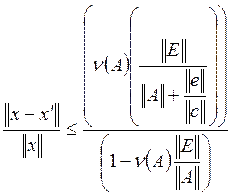
Здесь 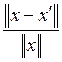называется относительной погрешностью в решении х,

называется относительной погрешностью в матрице A ,  называется относительной погрешностью в правой части с.

Часто, чтобы оценить точность полученного приближенного решения х’, вычисляют вектор невязки r = b – Ax’. Оценим относительную погрешность решения через невязку r.

 

3. Описание метода

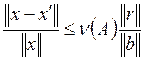Пусть требуется решить линейную систему Ax = C:

a₁₁x₁ + a₁₂x₂ + … + a_1nx_n = c₁,

                                 a₂₁x₁ + a₂₂x₂ + … + a_2nx_n = c₂,                                   (1)

                                                   …

                                 a_n1x₁ + a_n2x₂ + … + a_nnx_n = c_n,

Метод Жордана состоит в том, что элементарными преобразованиями над строками матрицы она приводится к единичной, и тогда правая часть будет содержать искомое решение.

Предположим, что a₁₁  отличен  от нуля. Поделив первое уравнение системы на a₁₁, перепишем его в виде:

x₁ + a₁₁⁽¹⁾x₂ + … + a₁₁⁽¹⁾x_n = c₁⁽¹⁾,

где a_1j⁽¹⁾= a_1j/  a₁₁, j=2,…,n,  c₁⁽¹⁾ = c₁/ a₁₁.  Умножив это уравнеие на a_i1 и вычтем из i-го уравнения системы (i = 2,…,n). В результате система примет вид

x₁ + a₁₂⁽¹⁾x₂ + … + a₁₁⁽¹⁾x_n = c₁⁽¹⁾,

a₂₂⁽¹⁾x₂ + … + a_2n⁽¹⁾x_n = c₂⁽¹⁾,                                 (1.1)

…

a_n2⁽¹⁾x₂ + … + a_nn⁽¹⁾x_n = c_n⁽¹⁾,

где   a_ij = a_ij - a_1j a_i1,    c_i⁽¹⁾ = c_i⁽¹⁾, - c₁⁽¹⁾ a_i1,   i, j = 2,…, n.

После k - 1,  k = 1,…,n шагов метода Жордана система преобразована к виду:

x₁                           + a_1k^(k-1)x_k + … + a_1n^(k-1)x_n = c₁^(k-1),

                                   x₂                      + a₂₂^(k-1)x_k + … + a_2n^(k-1)x_n = c₂^(k-1),

                                         ^.._.                                   …

                                              x_k-1 + a_k-1,k^(k-1)x_k + … + a_k-1,n^(k-1)x_n = c_k-1^(k-1),                 (2)