Анализ и синтез механизмов сенного процесса, страница 3

6)  Для определения скорости точки В- VВО2 воспользуемся теоремой подобия

 

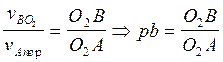Отрезок pb, обозначающий скорость vBO2, лежит на той же прямой, что и отрезок pa, и направлен в ту же сторону.

7)  для определения скорости точки С проводим из точки b прямую, перпендикулярную звену ВС, до пересечения с прямой, проходящей через p и параллельной оси х- линии действия vc. Точку пересечения обозначим точкой С.

8)  получившийся отрезок pc соответствует абсолютной скорости движения точки С, т.к. vc=vB+vCB.

9)   Для определения движения скорости центра масс звена 4, делим отрезок pc пополам, и полученную точку S4 соединяем с полюсом P. Вектор PS4 соответствует скорости движения центра масс звена 4.

2.3.2.Аналитическое определение аналогов скоростей звеньев механизма.

Аналитическое определение аналогов скоростей основано на дифференцировании по обобщенной координате уравнений замкнутости контуров.

Рассмотрим 1 контур О1АО2О1. После дифференцирования системы уравнений (1) получаем:

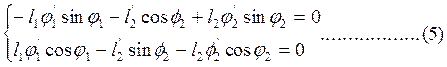Где j1-аналог угловой скорости звена 1. В расчетах j1=-1.

Выражаем из уравнений l2 и j2, при этом вычитаем из аргументов всех тригонометрических функций первого уравнения угол j1, а из второго - j2 и получаем следующие выражения:

Тогда :

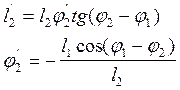Рассмотрим второй контур О2ВСDO2. После дифференцирования системы уравнений (2) получим:

Из первого уравнения получим:

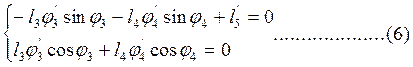А из второго:

Следовательно, мы можем найти следующие параметры:

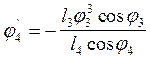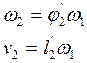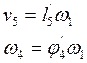После подставления численных значений получаем:

Аналоги скоростей центров масс звеньев 3 и 4 получаем в проекциях на оси координат, дифференцируя по обобщенной координате системы уравнений уравнений (3) и (4):

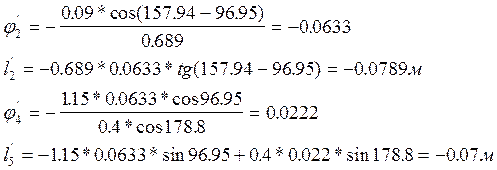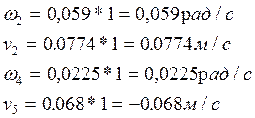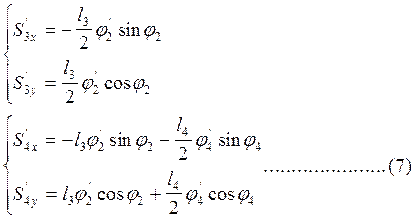Все вычисленные по формулам величины сравниваем с соответствующими величинами, найденными из плана скоростей механизма. Результаты сравнения приведены в таблице.

Из плана скоростей имеем:

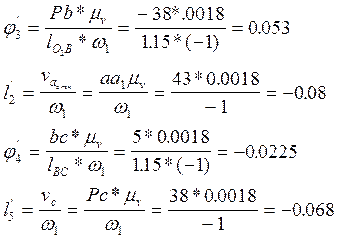Величина	j3	l2,м	j4	l5, м
Из плана скоростей	0,076	0,078	-0,029	0,086
Аналитическая	0.076	0.077	-0,03	0,086

2.4.Графическое и аналитическое определение аналогов ускорений.

2.4.1.Графическое определение аналогов ускорений.

План ускорений представляет собой лучевую диаграмму, позволяющую находить ускорения точек.

Порядок построения плана ускорений:

1.Определяем ускорение точки А. Полное ускорение точки А равно нормальной составляющей аА, которая направлена по линии О1А к центру О1.

Из точки p- полюса плана ускорений – откладываем вектор, изображающий ускорение точки, в виде отрезка pа1=30 мм;

3.Подсчитываем масштабный коэффициент ускорений:

4.Рассмотрим движение точки А вначале со вторым звеном, а затем с третьим:

Нормальное ускорение вычисляем по формуле:

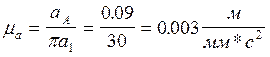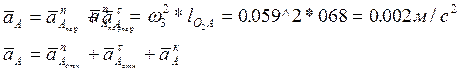Кориолисово ускорение определяем поформуле:

Отрезки, изображающие в миллиметрах векторы этих ускорений, равны:

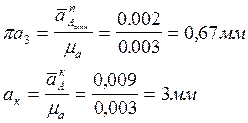Из точки а1 проводим прямую, перпендикулярную звену О2В. Вектор кориолисова ускорения будет направлен вдоль этой прямой к точке а1. Откладываем на этой прямой вектор ак в масштабе. Через точку ак проведем прямую параллельную звену О2В. Вектор аАотн находится на этой прямой и направлен к точке ак. Из точки p на прямой параллельной звену О2В отложим отрезок pа3, соответствующий аАпер, направленный к О2.

Из точки а3 проведем прямую на которой, находится аАпер. На пересечениях прямых, соответствующих аАотн и  аАпер, находится точка а. Полученные отрезки соответствуют: pа – общий вектор ускорения точки А, pа3 – аАотн, аа3 – аАпер.

Найдем эти ускорения:

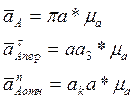5.Для определения ускорения точки В звена 3 используем теорему подобия:

6.Ускорение точки С находится из уравнения:

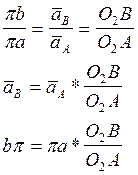Нормальное ускорение направлено параллельно звену ВС к точке В и равняется:

Касательное ускорение лежит на прямой перпендикулярной ВС и проходящее через точку с1. Ускорение ас находится на прямой параллельной оси х и проходящей через p. На пересечении этих двух прямых находится точка с. Тогда:

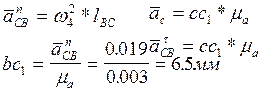7.Из плана ускорений находим:

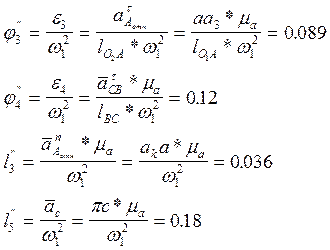 2.4.2.Аналитическое определение аналогов ускорений.

Определение ускорений аналитическим методом основано на дифференцировании по обобщенной координате уравнений (5) и (6).

После дифференцирования уравнений (5) получим:

Из первого уравнения системы найдем аналог относительного ускорения второго звена, для этого вычтем из аргументов всех тригонометрических функций угол j2 :

Из второго уравнения системы найдем аналог углового ускорения второго звена, для этого вычтем из аргументов всех тригонометрических функций угол j2 :

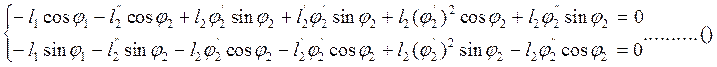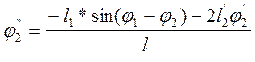Рассмотрим 2 контур О2ВСDO2. После дифференцирования выражения (6) будем иметь:

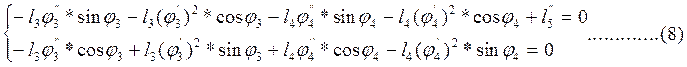Из первого уравнения системы найдем аналог относительного ускорения пятого звена, при этом вычтем из аргументов всех тригонометрических функций угол j4 :

Из второго уравнения системы найдем аналог углового ускорения пятого звена, для этого вычтем из аргументов всех тригонометрических функций угол j4 :