Анализ и синтез механизмов сенного пресса, страница 3

При дифференцировании уравнений (2.7) учитываем, что j₂’ = j₄’, а вектор l₀ не зависит от обобщенной координаты, в итоге получаем

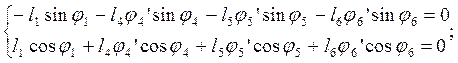                                          (2.22)

Выразим из второго уравнения (2.21) j₂’:

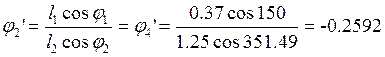                                                      (2.23)

и подставив в первое, найдем l₃’:

           (2.24)

Из уравнений (2.22) соответственно находим j₅’, j₆’:

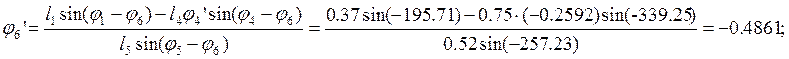(2.25)

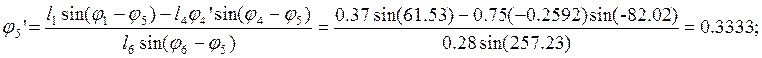   (2.26)

Аналоги скоростей центров масс звеньев 2 и 4 получаем в проекциях на оси координат, дифференцируя по обобщенной координате уравнения (2.19) и (2.20):

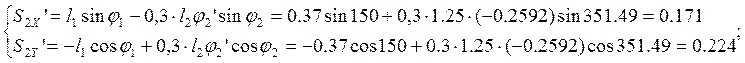          (2.27)

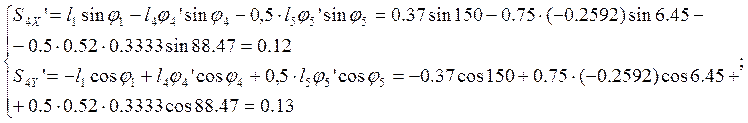     (2.28)

Значения аналогов скоростей для остальных положений механизма представлены в таблице 2.3

Аналитическое определение аналогов ускорений основано на дифференцировании по обобщенной координате уравнений (2.21) и (2.22):

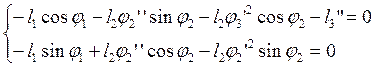                                                       (2.29)

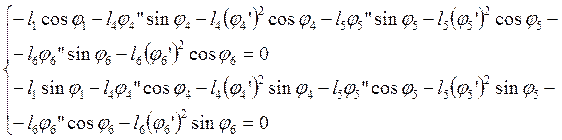                        (2.30)

Выражаем из второго уравнения (2.29) j₂”:

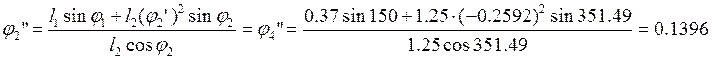    (2.31)

подставляем в первое и находим l₃”:

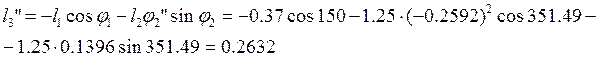                  (2.32)

        Из уравнений (2.30) выражаем соответственно j₅” иj₆”:

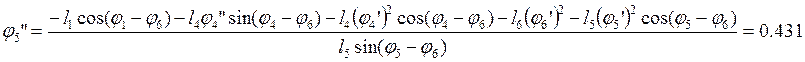(2.33)

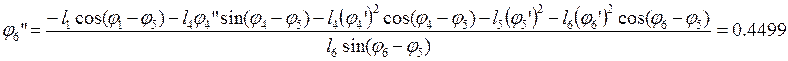(2.34)

Дифференцируя по обобщенной координате уравнения (2.27) и (2.28), определяем аналоги ускорений центров масс звеньев 2 и 4 в проекциях на оси координат:

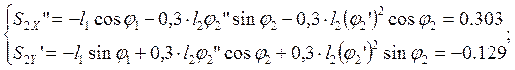                                 (2.35)

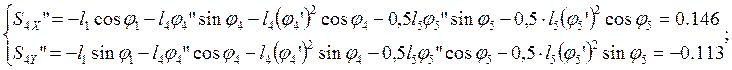  (2.36)

Результаты расчета аналогов ускорений для всех положений приведены в таблице 2.4.

2.5. Построение планов скоростей и ускорений.

2.5.1. Определение аналогов скоростей исследуемого станка графическим методом

Решение этой задачи графическим методом основано на построении плана скоростей для первого положения механизма при . Так как аналоги скоростей и ускорений не зависят от закона изменения обобщенной координаты, принимаем w₁ = 1 рад/с.

План скоростей строим в следующем порядке:

1) находим скорость точки А:

;

2) из полюса плана скоростей р – откладываем отрезок ра = 74мм, изображающий вектор скорости точки А;

3) подсчитываем масштабный коэффициент плана скоростей:

;

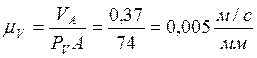4) Скорость точки  B, находим путем сложения абсолютной скорости точки A и относительной скорости точки B :

,          где ,      и                        (2.37)

Уравнение (2.37) решаем графически. Через точку а проводим линию, перпендикулярную AВ, до пересечения с осью OX, таким образом получаем точку b. Векторы рb  и аb изображают искомые скорости (абсолютная) и (относительная);

5) Скорость точки С звена 2 определяем, используя теорему подобия  

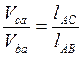,                                                                                   (2.38)                              

откуда

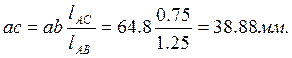
Отрезок aс откладываем перпендикулярно линии ACот точки a;

6) Для определения скорости точки D раскладываем плоскопараллельное движение звена 4 на переносное вместе с точкой Cи относительное вокруг точки C:

, где    и   .

Через точку с проводим линию перпендикулярную CD, а через полюс p – линию, перпендикулярную звену DO₁, до пересечения их в точке d. Вектор pdи cd изображают  искомые скорости точки d -  и ; 

7) положения точек E, S₂ и S₄ на плане скоростей находим, воспользовавшись теоремой подобия:

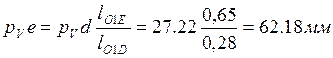
Векторы ps₂, pe и ps₄ изображают скорости ,  и .

8)  Из плана скоростей находим:

 

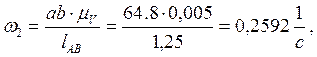
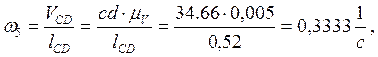
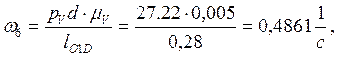
Определяем аналоги линейных и угловых скоростей:

                                     

                                         

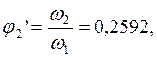
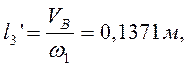
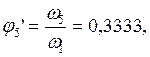
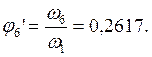
В табл. 2.3 приведены значения аналогов скоростей, полученные графическим и аналитическими методами:

Таблица 2.3.

Результаты расчета аналогов скоростей.

Величина	j2’°	l3’, м	j5’°	j6’°	S2X’, м	S2Y’, м	S4X’, м	S4Y’, м
Графически	0.2592	0.1371	0.3333	0.4861	–	–	–	–
Аналитически	-0.2592	0.1371	0.3333	-0.4861	0.171	0.224	0.12	0.13
Отклонение, D %	0	0	0	0	0	0	0	0

2.5.2. Определение аналогов ускорений исследуемого станка графическим методом.

Задачу решаем путем построения плана ускорений, считая w₁ постоянной величиной:

1) Определяем ускорение точки А. Полное ускорение точки А равно нормальной составляющей, , которая направлена по линии О₁А к центру А

, так как .

.

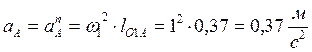2) Из точки p полюса плана ускорений – откладываем вектор, изображающий ускорение точки А, в виде отрезка pа = 92.5 мм.

3) Подсчитываем масштабный коэффициент ускорений:

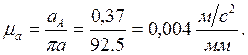
4) Ускорение точки В находим из уравнения:

                                                                                        (2.39)

где      – абсолютное ускорение точки А, ;

 – абсолютное ускорение точки B, 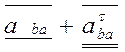 - нормальное и тангенциальное ускорения точки Bвокруг точки А, , отрезок, изображающий вектор этого ускорения, равен: .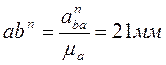

Уравнение (2.39) решаем графически. Проведем линию, параллельную ОА из полюса плана ускорений. Вектор ускорения а_а направлен к центру О. Из точки а проведем параллельно AB отрезок abⁿ. Из точки bⁿ проведем отрезок, перпендикулярный AB до пересечения с осью OX. В результате получаем точку b. Отрезок pb изображает абсолютное ускорение точки B. Отрезок bⁿb – тангенциальное ускорение точки BвокругA.

n₁b=43.62мм                       

                                            e₂ = a^t_ba/l_ab = 0,1396c^-2

pb=65.8 мм;                         

5) Ускорение точки С звена 2 определяем, используя теорему подобия  

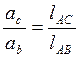,                                                                                                   (2.38)

6)   Для определения ускорения точки D составим уравнения:

                                                                                   (2.40)