Вопрос 2. Преобразование тензоров механических напряжений и деформации. Расчет механических напряжений и деформаций с помощью тензорного калькулятора.
Тензор механических напряжений
Объем твердого тела, находящийся в напряженном состоянии, в общем случае испытывает влияние сил двух типов: 1) объемных сил, действующих на все части упругого элемента, таких как силы инерции или сила тяжести, величина которых пропорциональна объему элемента; 2) сил, действующих через поверхность любого элементарного объема упругого элемента со стороны окружающих частей. Такие силы пропорциональны площади поверхности. Величина силы, отнесенная к единице площади, именуется напряжением.
Пусть в теле упругого элемента выделена малая площадка δSи ее ориентация в пространстве задается с помощью вектора внешней нормали l (111213). Равнодействующую сил на площадке δS обозначим F, тогда отношение F/ δS = Tдает вектор механических напряжений, действующих на эту площадку (рис. 1).
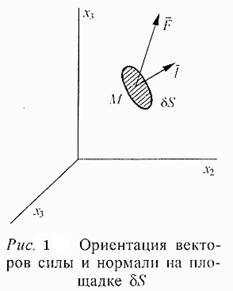
В пределе, при δS→ 0, вектор напряжений описывает силовое воздействие в точке M(x1x2x3) твердого тела. Для описания напряженного состояния твердого тела удобно использовать 9 коэффициентов преобразования, связывающих компоненты вектора напряжения и вектора нормали к площадке δS в точке М:
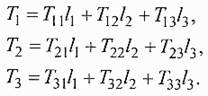 , где Tij – тензор второго ранга, именуемый тензором механических
напряжений.
, где Tij – тензор второго ранга, именуемый тензором механических
напряжений.
Тензор механических напряжений при преобразовании координат (повороте) изменяется согласно уравнениям:
![]()
где [α] - матрица направляющих косинусов, связывающих «старую» и «новую» системы координат. Эта матрица строится по правилу:

где αij = cos (xi’, xj) и т.д.
Матрица направляющих косинусов обладает несколькими важными свойствами, позволяющими контролировать правильность ее составления:
![]()
Величина, стоящая в правой части формулы - дельта-символ Кронекера, определяемый равенством:
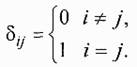
Транспонированная матрица направляющих косинусов является одновременно и обратной по отношению к исходной, что приводит к равенству:

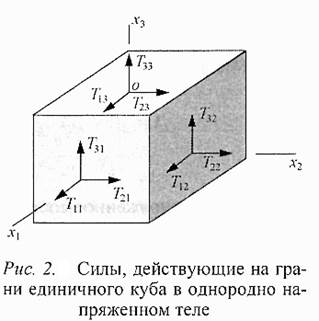
Физический смысл компонент Tijочевиден из рис. 2, где представлены силы, действующие на грани единичного куба в однородно напряженном теле. Через каждую грань будет передаваться сила, действующая со стороны внешних частей тела на внутреннюю область куба. Силу, приложенную к каждой грани, можно разложить на три компоненты. Тогда Tijозначает i-ю компоненту, действующую в направлении оси охi, на грань куба, перпендикулярную к охj. Диагональные компоненты T11, T22, T33 именуются также нормальными компонентами и описывают напряжения растяжения или сжатия на площадях, перпендикулярных к осям (x1,x2,x3). Недиагональные компоненты описывают сдвиговые механические напряжения, когда сила действует касательно плоскости соответствующей площадки. Сдвиговые компоненты стремятся исказить форму единичного куба.
Тензор деформации.
Упругие элементы микромеханических систем, находящиеся в напряженном состоянии, деформируются, т. е. расстояние и взаимная ориентация двух любых точек, относящихся к упругому элементу, изменяются. В теории упругости смещения любой точки твердого тела при деформации описываются с помощью вектора смещения u,компоненты которого в общем случае зависят от положения точки в недеформированном теле, u (x1,x2,x3)
При исследовании разнообразных физических явлений в микросистемной технике ключевое значение имеет не абсолютное смещение точек, а их относительное перемещение и, следовательно, относительные деформации. Кроме того, практическое значение имеют только малые смещения, что обусловлено, в первую очередь, хрупким характером разрушения кремния.
Для пояснения идеи математического описания деформации рассмотрим растяжение тонкой пластинки (рис. 3). Выберем систему координат и зафиксируем ее в пространстве (система координат неподвижна!). Под действием механических напряжений пластинка деформируется и точка М с координатами (x1,x2) перемещается в точку М' с координатами х1 + и1 и х2 + и2.
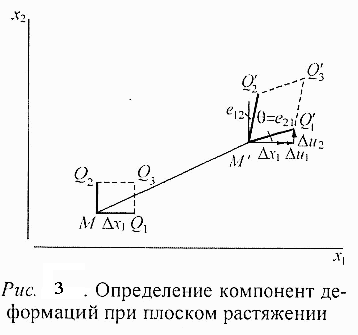
Величины и1 и u2 - компоненты вектора смещения точки М, u (u1, u2)в выбранной системе координат. Выделим на недеформированной пластинке малую прямоугольную область МQ1Q2Q3, со сторонами ∆x1 и ∆х2, параллельными осям х1 и х2. После деформации эта область изменяет свои размеры и форму и имеет обозначение М’Q1’Q2’Q3’. Отрезок ММ' представляет собой вектор смещения точки М. Изменение размера проекции отрезка МQ1’на ось х1 можно охарактеризовать отношением
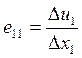 .
.
Поворот отрезка МQ1’ относительно оси х1 можно охарактеризовать углом:
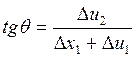 .
.
Поскольку
углы поворота малы (следствие малости деформации), tgѲ≈Ѳ и в
знаменателе ∆u1<<∆x1, получаем 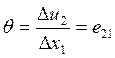 .
.
Аналогично, изменение размеров и положения стороны М’Q2’, можно получить соотношения :
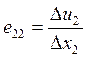
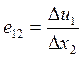 .
.
В пределе при ∆х1 и ∆х2 → 0, четыре безразмерные величины еij характеризуют деформацию пластинки в точке. Более точно деформированное состояние упругого элемента описывает тензор деформации Ɛij, построенный как симметризованная комбинация из еij:
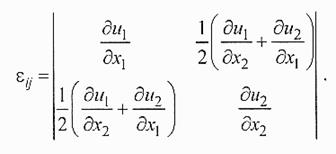
Применение симметризованных комбинаций частных производных позволяет исключить не интересные для теории упругости вращения пластинки как целого, когда расстояние и взаимное положение точек упруго элемента не изменяются.
В случае трех измерений, когда вектор смещения точки М зависит от трех координат M(x1x2х3), общий подход к определению тензора деформаций, изложенный выше, полностью сохраняется. Трехмерный тензор деформаций определяется симметризо-ванными выражениями:
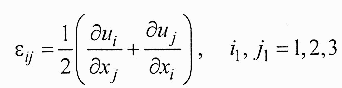
Диагональные компоненты описывают удлинение или сжатие сторон элементарного объема, остальные компоненты представляют сдвиговые деформации, характеризующие изменение углов между прямыми. Например, если в недеформированном упругом элементе две прямые образуют прямой угол, то после деформации угол будет равен φ = 0.5π-2ε13. Аналогично можно интерпретировать ε23 и ε31.
Задача.
Одноосное напряжение δ = 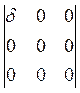 . L1 (112), δ
(МПа) = 95, L2 (313).
. L1 (112), δ
(МПа) = 95, L2 (313). 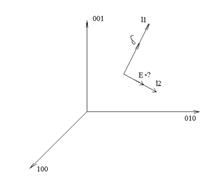
1. Построить ортогональную систему координат в которой х1 совпадает с l1.
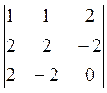 .
.
2. Построить матрицу перехода от этой с.к. к кристаллографической.
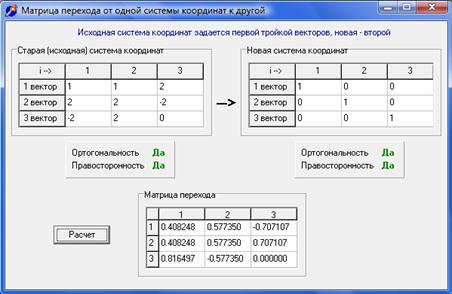
3. Преобразовать δ от исходной с.к. к кристаллографической.
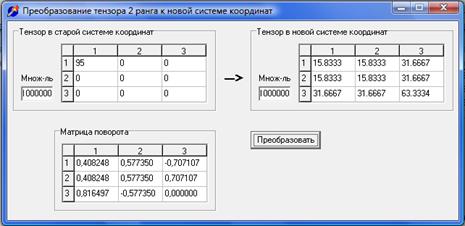
4. Привести тензор δ к одноосной форме.
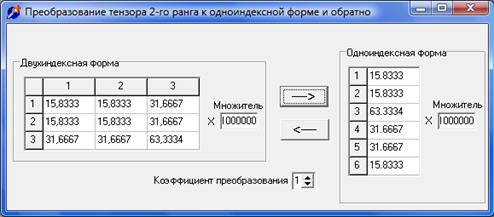
5. Выполнить закон Гука ![]()
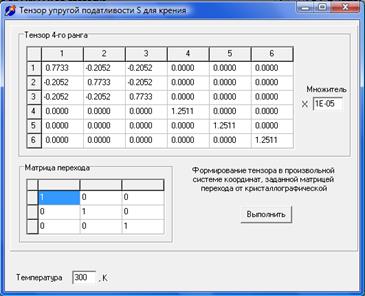
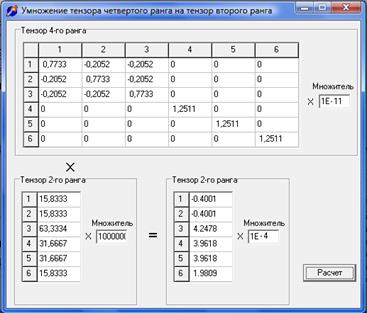
6. Преобразование Е к двухиндексной.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.