Дифференциальные уравнения. Линейное дифференциальное уравнение первого и второго порядка. Дифференциальные уравнения в полных дифференциалах, страница 4

           

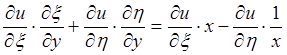
Возьмем вторую производную:

+

=

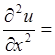
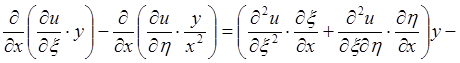
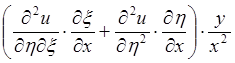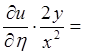
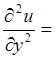
            Подставив в данное дифференциальное уравнение найденные для вторых производных выражения, получим уравнение приведенное к каноническому виду:

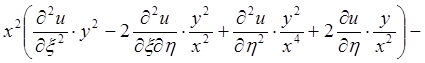
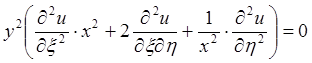
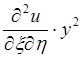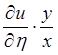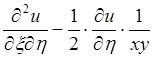-4+2= 0;     =0;    .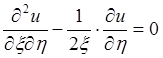

Уравнения математической физики

Физические основы

Многие проблемы классической физики приводят к отысканию решения f(x,t) линей-

ного уравнения с частными производными в заданном интервале или области (табл.2). Неизвестная функция u или ее производные должны в дополнение удовлетворять заданным начальным условиям при t = 0 и линейным краевым условиям на границе S (представляет координатную линию или поверхность) области D. Аналогичные проблемы возникают в квантовой механике.

Каждое дифференциальное уравнение, приведенное в табл.2, является однородным

(если произведение a×u любой постоянной a на решение u также является решением), если f(x; t)=0. Заданное краевое условие также однородно, если наряду с каждой функцией u, которая удовлетворяет краевому условию, ему удовлетворяет и функция a×u.

Неоднородности возникают в результате действия внешних влияний (силы, источники тепла, электрические  заряды или токи) на рассматриваемую физическую систему.

Запишем  уравнение второго порядка в общем виде:

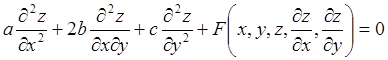
где а, b, с—функции х и у.

Говорят, что указанное уравнение в области D принадлежит:

¨ гиперболиче­скому типу, если в этой области b²—ас > 0;

 ¨ параболическому типу, если в этой области b²—ас = 0;

¨ эллиптическому типу, если в этой области b²—ас <0;

·  Эллиптическое дифференциальное уравнений описывает типичные стационарные процессы (стационарные температурные и электростатические поля, упругая деформация).

· Параболическое и гиперболическое дифференциальные уравнения описывают:

¾  переходные процессы (свободные колебания, возникающие вследствие заданных начальных возмущений) или,

¾ если имеются неоднородности, зависящие от времени, то описывают процессы распространения возмущений (вынужденные колебания, излучение).

Можно связать каждую проблему обсуждаемого типа со своей аппроксимирующей

системой  обыкновенных дифференциальных уравнений.                                          

Важнейшие линейные одномерные дифференциальные уравнения Таблица 2.

Тип	Физический смысл	Одномерное уравнение	Дополнительные условия
Параболический	Уравнение теплопроводности, диффузии		краевые условия; начальные условия для u
Гиперболический	Волны (струны, мембраны, течение жидкости), затухающие волны.  Телеграфное уравнение		краевые условия; начальные условия для u и ¶ u/¶ t
Эллиптический	Статический случай		только краевые условия
Уравнения 4-го порядка	Упругие колебания		краевые условия; начальные условия для u и ¶ u/¶ t
	Статический случай		только краевые условия

Решения некоторых уравнений математической физики

1⁰. Уравнение колебания струны ( методом Даламбера)

Функция  u=u(x,t) удовлетворяет дифференциальному уравнению 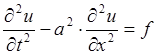,  где

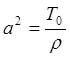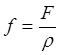,  ,  T₀-начальное натяжение струны,- линейная плотность струны, F – сила, действующая на струну перпендикулярно оси абцисс и рассчитанная на единицу длины.

            Если внешняя сила отсутствует, т.е. f=0, то получится уравнение свободных колебаний струны  .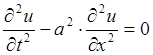

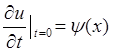Зададим начальные условия задачи: - форма струны, -скорость струны в виде функций абцисс х этих точек. 

После введения новых переменных x(кси) = x - at, h(эта) = x + at и приведения уравнения к каноническому виду (см. Лекция № 4) имеем: .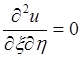

Решение этого уравнения (см. Лекция № 4, пример № 16)имеет вид: , где q₁ и q₂ – произвольные функции.

Подобрав функции q₁ и q₂ так, чтобы функция u=u(x,t) удовлетворяла начальным граничным условиям, придем к решению исходного дифференциального уравнения в виде:

                       

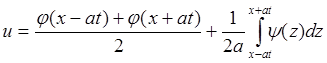
Пример 27.   Найти форму струны, определяемой уравнением 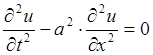в момент

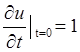t =p/2a, если - форма струны, - скорость струны.

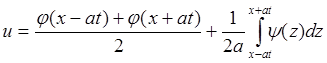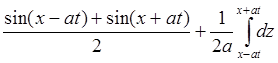
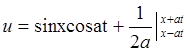== sinx×cosat + t. В момент времени t = p/2a  u = p/2a.

2⁰. Уравнение колебания струны ( методом Фурье)

Найти решение уравнения .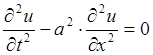

Начальные граничные условия: , , , .

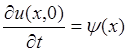Решение уравнения ищется в виде произведения двух функций: , u(x,t)¹0,

тогда u¢_t(x,t)=X(x)×T¢(t), u¢¢_t(x,t)=X(x)×T¢¢(t) u_x¢(x,t)=X¢(x)×T(t), u_x¢¢(x,t)=X¢¢(x)×T(t),  и XT¢¢ = a²X¢¢T , 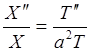   соотношение возможно, если обе части есть одна и та же постоянная (обозначим её m = - l²).

 и Þ  Общие решения: ,

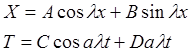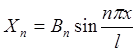Из краевых условий X(0)T(t₀) = X(l)T(t₀)=0, то X(0)=A=0 Þ X=Bsinlx, X(l)=Bsinll=0, l= Þ  , T_n 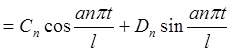. Каждому  С_n и D_n соответствуют свои a_n и b_n (c включенным в них B_n), тогда решение может быть представлено как сумма бесконечного ряда:  u(x,t)=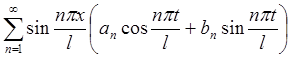, где

  ;   ,

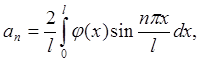
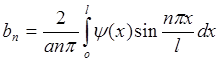3⁰.Уравнение теплопроводности

Уравнение теплопроводности для двумерного стационарного случая обращается в уравнение Лапласа  +=0, (u - функция точки и не зависит от времени).

С уравнением Лапласа связано понятие гармонической функции – функции непрерывной вместе со своими производными до второго порядка включительно и удовлетворяющую уравнению Лапласа.

Задача отыскания функции u непрерывной в области D ( включая и поверхность S, ограничивающую эту область) и удовлетворяющей граничному (краевому) условию  ( f(x,y)- заданная непрерывная на S функция) называется задачей Дирихле.

Стационарная задача

Пример 28.  Найти стационарное распределение температуры в тонком стержне с теплоизолированной боковой поверхностью, если на концах стержня ,  .

            Задача Дирихле для одномерного случая состоит в нахождении уравнения Лапласа 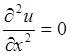 функции u, удовлетворяющей заданным краевым условиям.

            Общее решение уравнения: 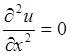, , 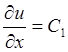u=С₁×_×x+С₂ .

 После подстановки краевых условий имеем:  , ,  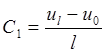Þ

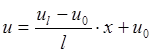  . Температура вдоль стержня распространяется линейно.

Нестационарная задача

Если тело является стержнем, направленным вдоль оси 0х, то уравнение теплопроводности для нестационарного случая имеет вид: .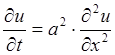

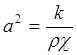, где k-коэффициент теплопроводности, r-плотность среды, l-теплоемкость среды.

Найти решение u(x,t) уравнения 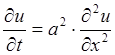, t > 0, -¥ < x< +¥

Начальные условия: u(x,0)=f(x), -¥ < x< +¥

Концы стержня погружены в тающий лед, т.е. в них поддерживается постоянная температура и граничные условия:  u(o,t)=u(l,t)=0.

Задача решается  методом Фурье.

4⁰.Задача Дирихле для круга

Эта задача решается нахождением уравнения Лапласа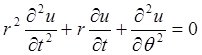

методом Фурье  с граничным условием , f(q )- заданная функция на окружности круга радиусом R.

Подставив u в уравнение Лапласа, разделив переменные и приравняв обе части к постоянной m = –l² , получим решение для функции u(r,q ) при заданных граничных условиях :

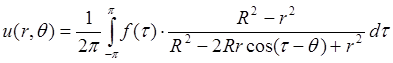- интеграл Пуассона

(При разложении функции f(q) в ряд Фурье, коэффициенты Фурье определялись по известным формулам (Лекция № 5) на промежутке [-p;p].)