Множества и операции над ними. Соответствия и функции, отношения

1. МНОЖЕСТВА И ОПЕРАЦИИ НАД НИМИ

Дискретная (конечная) математика  - это математика не связанная с понятиями бесконечности, предела и непрерывности. В данном курсе мы будем рассматривать исключительно конечные множества.

Понятие множества принадлежит к числу фундаментальных, неопределяемых понятий математики. Можно сказать, что множество – это любая определённая совокупность объектов. Объекты, из которых состоит множество, называются – элементами.

Примеры: множество N натуральных чисел; множество P простых чисел; множество Z целых чисел; и т. п.

Если объект х является элементом множества М, то это обозначается , если объект х не является элементом множества М, то это обозначается .

Обычно множества обозначают прописными буквами алфавита, а их элементы – строчными.

Множества, как объекты, тоже могут быть элементами других множеств. Множество, элементами которого являются множества, называют классом или семейством множеств. Семейства обычно обозначают большими рукописными буквами A,B,D, и т.д. Множество, не содержащее элементов – пустое множество  Æ. Противоположное ему понятие универсального множества или универсума U – достаточно широкого фиксированного множества, которое содержит элементы всех множеств, которые мы будем рассматривать.

1.1  Способы задания множеств

Задание множеств – это указание того, какие элементы принадлежат множеству. Способы задания:

1.  перечисление элементов – M:={a₁,a₂,…,a_n}

2.  характеристический предикат M:={х½ P(x)} - это некоторое условие, выраженное в виде логического утверждения;

3.  порождающая процедура - M:={х½ x:=f(x)}

Примеры:       M:={1,2,3,4,5,6,7,8,9}

M:={ х½ xÎN &  х<10}

M:={ х½ for x from 1 to 9 yield x}

Перечислением задаются только конечные множества. Бесконечные -предикатами или порождающими процедурами.

Два множества А и В равны тогда и только тогда, когда

Р_А(х)Р_В(х).                                             (1.1.1)

Пример: А – множество студентов второго курса. В – множество прошлогодних первокурсников, успешно сдавших 2 сессии, и студентов восстановленных после академического отпуска. Очевидно, что Р_А(х)Р_В(х)так как речь идёт об одних и тех же людях.

1.2 Сравнение множеств.

Множество А содержится в множестве В, если каждый элемент множестваАодновременно является элементом множества В.

А Ì В:= х Î А  Þ  х Î В                                          (1.2.1)

В этом случае А – подмножество множества В, а В – надмножество множества А.  Если А Ì В и А ¹ В , то А называют собственным подмножеством В(несобственные подмножества обозначаются Í). Для любого множества М   Æ Ì М и М Í М.

Другое определение равенства множеств:

А=ВеслиА Í В & В Í А(1.2.2)

Мощность множества обозначается  и равна (для конечных множеств) числу элементов, содержащихся в этом множестве. Если , то такие множества называются равномощными.

Пример:          1.½Æ½=0, но ½А:={Æ}½=1, так как это множество состоит из множеств.

                          2. Для M:={ & х<10} .½М½=9

1.3  Операции над множествами

Операции над множествами – это способ конструирования множеств из уже имеющихся.

Объединение  -  АÈВ:={х½хÎА Ú хÎВ}

Пересечение  -  АÇВ:={х½хÎА & хÎВ}

Разность  –  А\В:={х½хÎА & хÏВ}

Симметрическая разность - АDВ = (АÈВ) \ (АÇВ)

АDВ :={х½х Î А  &  х Ï В или х Ï А &  х Î В}

Дополнение :={х½х Ï А}

 

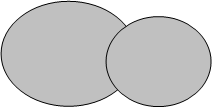Картинки, иллюстрирующие операции над множествами, называют диаграммами Эйлера или Виена.

Для всякого множества А может быть построено множество всех подмножеств множества А. Его называют булеаном и обозначают

2^А:={Х½Х Í А}(1.3.1)

Пример: Для множества А={a,b} булеаном будет множество 2^А:={{a},{b},{a,b},Æ}

Для построения булеана могут быть рассмотрены семейства мно-жеств, таким образом могут получиться «башни булеанов» ,  и т.п.

Теоремадля конечного множества Мвыполнено ç2^Мç=2^çМç

1.4 Свойства операций над множествами.

Пусть задан универсум U, тогда для любых   А, В, С Ì U

1.  идемпотентность                   АÈА=А или АÇА=А

2.  коммутативность                  АÈВ=ВÈА или АÇВ=ВÇА

3.  дистрибутивность                 АÈ(ВÇС)=(АÇВ)È(АÇС) или АÇ(ВÈС)=(АÇВ)È(АÇС)

4.  ассоциативность                   АÈ(ВÈС)=(АÈВ)ÈС или АÇ(ВÇС)=(АÇВ)ÇС

5.  поглощение                             АÈ(ВÇА)=Аили АÇ(ВÈА)=А

6.  свойства нуля                         АÇÆ=Аили АÈÆ=А

7.  свойства единицы                 АÇU=Аили АÈU=U

8.  инволютивность                    =А

9.  свойства дополнения           ÈА=Uи ÇА=Æ

10.  выражение для разности    А\В=АÇ

11.  законы де Моргана               или .

1.5  Разбиения и покрытия.

Пусть E={E_i} – некоторое семейство подмножеств М, где Е_iÌМ.Семейство называется покрытием множества М, если каждый элемент М принадлежит хотя бы одному из Е_i

МÎÛ" x Î M  $   i Î I  x Î E_i                       (1.5.1)

Семейство Eназывается дизъюнктным, если элементы этого семейства попарно не пересекаются, т.е. каждый элемент множества М принадлежит не более чем одному элементу E_i.

"   i, j Î I    i ¹ j    E_i Ç E_j = Æ(1.5.2)

Дизъюнктное покрытие множества М называется разбиением множестваМ.

Пример: Пусть множество М:={1,2,3},тогда множества E₁:={{1,2},{2,3},{1,3}}иE₂ :={{1},{2,3},{1,3},{1,2,3}}– являются покрытиями, а семействоE₃:={{1},{2},{3}} – разбиением множества М.

1.6  Кортеж. Декартово произведение множеств.

Неупорядоченной парой на множествах А и В называется любое множество {a, b}, где  а Î А  и  b Î В.

Если А = В, то говорят о неупорядоченной паре на множествеА.

Неупорядоченная пара{a, b}равна неупорядоченной паре {c, d},еслиa=cиb=dилиa=dи b=c. Если в неупорядоченной паре а=b, то она вырождается в одноэлементное множество {a}.

Упорядоченной парой (а, b)на множествах А и Вназывается пара элементов а Î А и b Î В, которая определяется порядком записи. Если А = В, то говорят, об упорядоченной паре на множестве А. Две упорядоченные пары(a, b)и (c, d)равны друг другу, еслиa = cиb = d.

Упорядоченную пару нельзя рассматривать, как множество из двух элементов!

Пример: Координаты точки на плоскости или в пространстве (в декартовой или полярной системах координат).

Обобщением понятия упорядоченной пары чисел является упорядоченный набор из n элементов или кортеж(а₁, а_2,…, а_n), где а₁ Î А₁,  а₂ Î А₂,…, а_b Î А_n.

Два кортежа  (а₁, а_2,…, а_n)  и  (b₁, b_2,…, b_n)  равны, если  а₁ = b₁, а₂ = b_2,…, а_n = b_n. Число n называют длиннойили размерностьюкортежа, а элементы a_i – i-тая проекцияили компонента кортежа.

Пример: Координаты точки пространства в декартовой или цилиндрической системе координат, координаты вектора.

Множество упорядоченных пар в которых первый элемент принадлежит А, а второйВ – называется прямым (Декартовым) произведением множеств

 А´В:={(а,b) | аÎА & bÎВ}(1.6.1)

Следует заметить, чтоX´Y¹ Y´Х.

Пример: Пусть Х={1,2}. Y={1,3,4}.

Тогда X´Y = {(1,1),(1,3),(1,4),(2,1),(2,3),(2,4)}

Степенью множества А называется его прямое произведение самого на себя

Аⁿ=А´А´¼´А                                     (1.6.2)

Теорема                       

Доказательство:           Так как  - множество упорядоченных пар, то каждый элемент аможно выбрать  способами. Каждому элементу а соответствует b, выбранный  способами. Следовательно, пару (а,b) можно выбрать  способами.

Следствие                

Аналогично: Множество всех кортежей длины n на множествах      А₁, А₂,…А_n называют декартовым (прямым) произведением множествА₁´А₂´…´А_n .

Свойства прямого произведения:

1.  А´(ВÇС)=А´ВÇА´С

2.  А´(ВÈС)=А´ВÈА´С

3.  А´Æ=Æ´А=Æ

Докажем 1. методом « двух включений». Пусть (х,у) Î А´(ВÇС), тогда у Î(ВÇС), а х Î А. Другими словами или у Î В или у Î С, тогда (х,у) Î А´В или А´С   Þ  (х,у) Î А´ВÇА´С.  Получаем А´(ВÇС)  Í  А´ВÇА´С .

Обратное включение: пусть (х,у) Î А´ВÇА´С, тогда (х,у) Î А´В или А´С, то есть или у Î В или у Î С, а х Î А.  Другими словами (х,у) Î А´(ВÇС). и так как А´ВÇА´С  Í  А´(ВÇС), тогда А´ВÇА´С = А´(ВÇС). Что и требовалось доказать.