Элементы векторной алгебры

§ 4. ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ

Многие задачи механики связаны с операциями над векторами. Поэтому целесообразно рассмотреть некоторые свойства векторных величин и правила операций над ними.

Известно, что физические величины, полностью оп­ределяемые одним числом, не зависящим от выбора сис­темы координат, называются скалярными. Иногда их называют абсолютными скалярами или инвариантами. Такие величины геометрически изображаются точками некоторой числовой оси. Примерами скалярных величин являются масса тела, энергия, температура и т. д

Векторные величины, кроме абсолютного числен­ного значения, характеризуются определенным на­правлением в пространстве. Различают связанные векторы, приложенные к определенной точке про­странства (например, вектор силы, действующей на деформируемое тело), скользящие векторы, которые можно перемещать вдоль некоторых прямых (сила, приложенная к абсолютно твердому телу), и, наконец, свободные векторы, не связанные физически с какой-либо определенной точкой пространства.

Существует два метода выполнения математиче­ских операций над векторами. В первом из них опера­ции выполняются непосредственно над векторами, не связывая их с системой координат. По этой причине метод называется бескоординатным. Второй метод на­зывается координатным. В этом методе математиче­ские операции производят не непосредственно над векторами, а над скалярными величинами, опреде­ляющими вектор в некоторой координатной системе.

1. Проекция вектора на ось и на плоскость. Рас­смотрим вектор   и ось Ох (рис. 1.11), не лежащие в общем случае в одной плоскости.

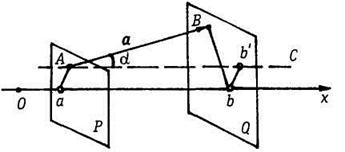
Рис. 1.11

Пусть А и В обозначают соответственно начало и конец вектора . Проведем через эти точки две плос­кости Р и Q, перпендикулярные к Ох, и отметим точ­ки а и  b  их пересечения с осью Ох. Отрезку аb можно доставить в соответствие положительное число, если направление отрезка совпадает с положительным на­правлением оси Ох, и отрицательное, если направле­ние отрезка ab противоположно направлению оси Ох. Этот отрезок или соответствующее ему число называ­ется проекцией вектора  на ось Ох.

Из точки А проведем прямую АС||Ох и обозначим через b' точку пересечения АС с плоскостью Q. Оче­видно, Аb' = аb. Пусть  означает наименьший угол между положительным направлением оси Ох и на­правлением вектора . Тогда проекция   вектора  на ось Ох будет:

 .                                                (4.1)

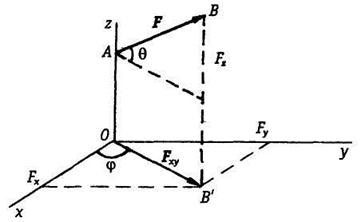
Рис. 1.12

Рассмотрим далее некоторый вектор  в пространстве с прямоугольной декартовой системой координат Oxyz (рис. 1.12). Проекцией вектора  на плоскость Оху называется вектор , заключенный между проек­циями начала А и конца В вектора  на эту плоскость.

Если  — угол между вектором  и его проекцией  на плоскость Oxy,  то модуль этой проекции опре­деляется формулой:

.                                           (4.2)

Зная модуль вектора , легко определить проек­ции вектора  на координатные оси:

;

;                                    (4.3)

,

где  - угол между вектором и положительным направлением оси Ох.

          2. Сложение векторов и разложение вектора на составляющие. Сумма нескольких векторов  есть вектор  (рис. 1.13,а), представляющий замыкающую ломаной   ABCDEF, составленной из слагаемых векторов:

.                                        (4.4)

      

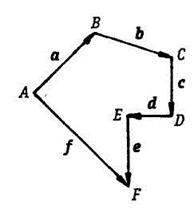
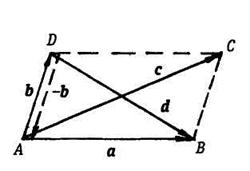
Рис. 1.13

В частности, сумма двух векторов  и  (рис. 1.136) есть вектор , являющийся диагональю АС параллело­грамма ABCD:

.                                                               (4.5)

Разность векторов  и  определяется как сумма вектора  и вектора, направленного противоположно , (рис. 1.13,б), т.е.

.                                    (4.6)

Рассмотрим вектор  в пространстве Охуz (рис. 1.14). Построим систему координат Ax'y'z', начало которой совместим с началом вектора , а оси Ах', Ay', Az' на­правим параллельно соответствующим осям системы Охуz. Пусть  — углы между вектором  и поло­жительными направлениями осей системы  Ох'у'z'. Тог­да проекции вектора  на оси Ох, Оу, Оz будут:

.                               (4/7)

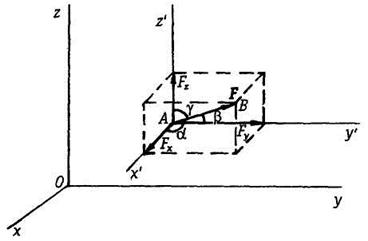
Рис. 1.14

Векторы , модули которых определяются формулами (4.7), а направления параллельны соответ­ствующей координатной оси Ох, Оу и Оz, называются составляющими вектора   по осям координатной сис­темы Охуz.

Таким образом, любой вектор  может быть един­ственным образом разложен на сумму трех векторов, если только эти три вектора не лежат в одной плоско­сти (не компланарны).

Обозначая единичные векторы (орты) прямоуголь­ной декартовой системы координат Охуz через  , можем представить:

.                                                          (4.8)

Проекции вектора  на оси Охуz называют также прямоугольными декартовыми координатами вектора  в системе  и обозначают так:

        или       .                       (4.9)

На основании известной из аналитической геометрии теоремы о проекции замыкающей ломаной линии координаты суммы векторов равны сумме координат слагаемых, так что формула (4.4) дает три скалярных равенства:

                                      ,

,                                     (4,10)

                                     .

3. Произведения векторов. Скалярным произведе­нием векторов  и  (обозначается ) называют ска­ляр, определяемый равенством:

.                                           (4.11)

где  — угол между векторами  и , приведенными к общему началу (рис. 1.15).

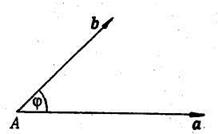
Рис. 1.15

Скалярное     произведе­ние векторов обладает сле­дующими свойствами:

а) - свойство переместительности;

б) - ( - скаляр)    свойство    сочетательности;

в) - для трех векторов свойство соче­тательности не имеет места;

г)     - свойство распределительности;

д) ;

е) ,  если  .

Скалярное произведение векторов  и  в координатах вычисляется по формуле:

.                                        (4.12)

Векторным произведением векторов  и  (обозна­чаются  или ) называется вектор , модуль которого  равен площади параллелограмма, построенного на векторах  и  как на сторонах, и на­правленный перпендикулярно  и  так, чтобы крат­чайший поворот  для совмещения с  казался наблю­дателю, смотрящему с конца вектора , идущим про­тив вращения часовой стрелки (рис. 1.16).

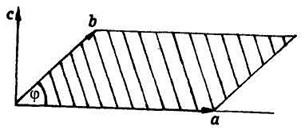
Рис. 1.16

Векторное произведение векторов обладает свойст­вами:

а);

б) , где  - скаляр;

в)  - не имеет место свойство сочетательности ;

г) -  свойство  распределительности;

д) , если  (условие коллинеарности векторов);

е)  .

Для векторов  и , заданных своими проекциями в прямоугольных декартовых координатах с ортами , векторное произведение вы­числяется по формуле:

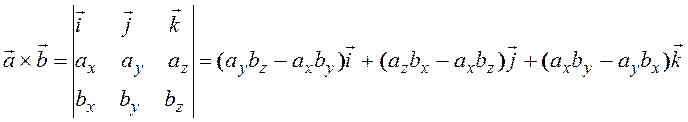  (4.13)