Электромагнитные колебания в простом колебательном контуре, страница 2

                                            (4)

Уравнение (4) – линейное дифференциальное уравнение второго порядка с обыкновенными производными и постоянными коэффициентами. Решения этого уравнения имеют различный вид в зависимости от соотношения между коэффициентами. Положим, что w₀>a , тогда:

                    (5)

где q₀ – максимальное значение заряда на обкладках конденсатора; j - начальная фаза колебаний; w - частота затухающих электрических колебаний:

.                      (6)

При R=0 и a=0

,

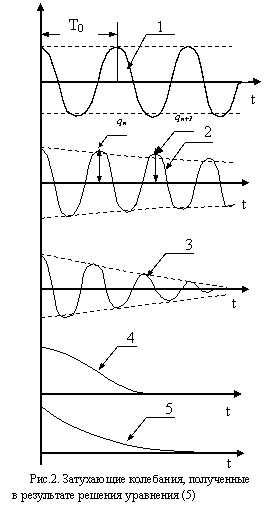
а период этих колебаний (рис.2, кривая 1) составляет:

.

В случае затухающих колебаний R¹0 (рис.2, кривая 2) и период:

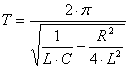.                          (7)

Решение (5) является аналитическим выражением затухающих колебаний. Большему значению коэффициента a соответствует кривая 3 (рис.2). Хотя затухающие колебания не являются периодическим процессом в строгом смысле этого слова, они обладают определённой повторяемостью в том смысле, что максимальные и минимальные значения заряда, а также тока и напряжения достигаются через одинаковый промежуток времени. Этот промежуток времени и называется периодом Т затухающих колебаний.

Для выяснения физического смысла коэффициента a рассмотрим тепловые потери W_R на сопротивлении R за полупериод Т/2:

,

где <Р> - среднее за период значение тепловой мощности, выделившейся на сопротивлении R. Для синусоидального тока:

.

Полный запас энергии колебательного контура:

.

Отношение энергии, израсходованной в контуре за полупериод на нагревание W_R (тепловые потери), к энергии колебаний W_L:

.

Используя обозначения (2),получим:

,

где q называется логарифмическим декрементом, который вместе с коэффициентом затухания характеризует потери энергии в контуре.

Как следует из (6), при a>w₀ частота w оказывается мнимой, т.е. колебаний в контуре не будет. Разряд конденсатора  будет апериодическим (рис.2, кривая 4 и 5). Логарифмический декремент может быть определён и другим путём. Пусть q_n и q_n+1 – амплитуды заряда конденсатора в момент времени t_n и t_n+1, причём t_n+1=t+T. Тогда ;  и, следовательно,

.

Как видно из полученного соотношения, отношения последующих амплитудных значений заряда не зависит от номера максимумов и является постоянной величиной для данного контура.

Прологарифмируем соотношение:

.                                                      (8)

Таким образом, логарифмический декремент контура можно определить, как натуральный логарифм отношения последующих амплитуд заряда конденсатора. В радиотехнической практике чаще пользуются величиной, обратно пропорциональной логарифмическому декременту q и называемой добротностью Q: