Число А називається границею функції y=f(x) при x®х0, якщо для всіх значень х, що достатньо мало відрізняються від числа х0, відповідні значення функції f(x) як завгодно мало відрізняються від числа А.
Позначення:
.
Функція y=f(x) називається нескінченно великою величиною при x® х0, якщо для всіх значень х, що достатньо мало відрізняються від х0 , відповідні значення функції f(x) за абсолютною величиною перевищують будь-яке наперед задане довільно велике додатне число:
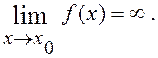
Функція, яка прямує до нуля при x® х0 , називається нескінченно малою величиною при x® х0
Якщо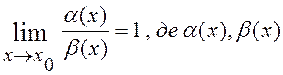 
-нескінченно малі (при х®х0), то a(х) і b(х) називаються еквівалентними нескінченно
малими (при х®х0).
Позначення:
a(х)~b(х) (х®х0).
1) Якщо функції f(x)і q(x) мають в точці х0 відповідно границі В
і С, то функції f(x)±q(x), f(x)×q(x),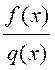
(при С¹0) мають в
точці х0 границі, що дорівнюють відповідно В ± С, В×С,
2) При обчисленні границі добутку функцій, одна з яких є нескінченно малою величиною, можна цю нескінченно малу величину замінити на еквівалентну їй величину.
Перша особлива границя:
.
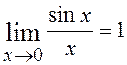Наслідки першої особливої границі:
1)
sinx~x (x®0),
2) tgx~x (x®0),
3) arcsinx~x (x®0),
4) arctgx~x (x®0),
5) 1-cosx~
(x®0).
Друга особлива границя:
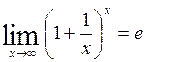(або 
)
Наслідки другої особливої границі:
1) ln(1+x)~x (x®0),
2) loga(1+x)~
(x®0),
3) ex-1~x (x®0),
4) ax-1 ~x lna (x®0).
Перед виконанням завдання № 5 рекомендується опрацювати приклади 6.1-6.18 глави ІІ.
§8. ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ ДО ЗАВДАННЯ №6
Література: [1], т. І, с.200-217, 239-260, [2], с.373-431, [3], с. 217-262, 341-377.
Похідною функції y=f(x)за аргументом x називають
границю відношення приросту функції Dy до приросту аргументу Dх, коли Dх довільним
образом прямує до нуля. Якщо ця границя існує, то її позначають через f’(x) або 
:
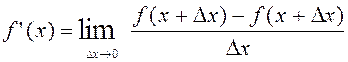
Операцію знаходження функції у = f(x) називають диференціюванням цієї функції. Функцію f(x), яка має похідну в точці x, називають диференційовною в точці x.
Якщо функція має похідну в кожній точці деякого проміжку, то її називають диференційовною у цьому проміжку.
Механічний зміст похідної: похідна S’(t) є величиною миттєвої швидкості в момент t тіла, що рухається за законом S=S(t).
Геометричний зміст похідної: похідна f’(x) дорівнює кутовому коефіцієнту дотичної до графіка y = f(x) в точці з абсцисою х.
Економічний зміст похідної: похідна V’(x) дорівнює маргінальній вартості, де V(х)-функція витрат виробництва х одиниць продукції.
похідних основних елементарних функцій
|
1.(xm)¢ = mxm-1 , m – будь-яке число, 2.(ex)¢= ex ; 3.(lnx)¢= 4.(sinx)¢=cosx ; 5.(cosx)¢=-sinx ; 6.(tgx)¢=1/cos2x ; |
7.(ctgx)¢=-1/sin2x ; 8.(arcsinx)¢= 9.(arccosx)¢=- 10.(arctgx)¢ = 11.(arcctgx)¢ = - |
Нехай С-постійна, u=u(x),v=v(x) - функції, що мають похідні. Тоді:
1) С’=0; 2)x'=1;3)(u±v) '=u'±v'; 4)(Cu) '=Cu';
5)(uv) '=u'v+uv';
6)
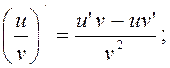
7)якщо y=f(u), u=u(x),тобто y=f[u(x)],де функції f(u )та u(x) мають похідні, то y'x = y'u×u'x.
(правило диференціювання складної функції).
Перед виконанням завдання № 7 рекомендується опрацювати приклади 7.1-7.12 глави ІІ.
§9. ОСНОВНІ ТЕОРЕТИЧНІ ВІДОМОСТІ ДО ЗАВДАННЯ №7
Література: [1], т. І, с.200-217, 239-260, [2], с.373-431, [3], с. 217-262, 341-377.
Правило, за яким кожній парі чисел (x;y)ÎDставиться у відповідність єдине число z, називається функцією двох змінних, що визначена на множині D.
Позначення: z= f (x,y).
Частинною похідною за змінною x від функції z=f(x,y) називається функція, яка одержана при диференціюванні f(x,y) за змінною x у припущенні, що y=const:
 |
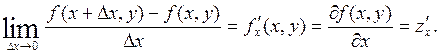Повним диференціалом функції двох змінних z=f(x;y)називається вираз
dz=
dx+
dy,
який є головною частиною повного приросту функції, лінійного відносно dx, dy.
Градієнт функції z в точці M(x0;y0):
 |
Похідна функції z в
точці М за напрямом вектора 
:
 |
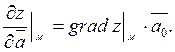Перед виконанням завдання № 7 рекомендується опрацювати приклади 7.21-7-26 глави ІІ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
.