Нахождение действительных корней нелинейных и трансцендентных уравнений. Численное решение дифференциального уравнения

СОДЕРЖАНИЕ

Введение.                                                                                     Стр.

1.  Нахождение  действительных  корней  нелинейных и  трансцендентных уравнений………………………………………

1.1. Метод  решения (Хорд)………………………………………….

1.2  Отделение корней  графическим  способом………………

1.3.  Алгоритм  решения  уравнения……………………………..

1.4.  Блок-схема  алгоритма…………………………………………   

1.5.  Текст  программы……………………………………………….

1.6.  Результаты  решения…………………………………………...

1.7.  Погрешность  найденного  решения……………………….

2.  Численное  решение  дифференциального  уравнения……..

2.1. Метод  решения (Рунге – Кутта )……………………………..

2.2. Алгоритм решения  уравнения……………………………….

2.3. Блок  - схема  алгоритма……………………………………….

2.4. Текст  программы………………………………………………..

2.5. Результаты  решения…………………………………………….

2.6. График  функции ……………………………………………….

3. Литература…………….…………………………………………………

  Введение

Численные  методы

С  помощью  математического  моделирования  решение  научно – технической  задачи  сводится  к  решению  математической  задачи , являющейся  ее моделью. Для  решения  математических  задач  используются  следующие  основные  группы  методов : графические, аналитические  и  численные.

Графические  методы  позволяют  в  ряде  случаев оценить  порядок  искомой  величины. Основная  идея  этих  методов  состоит  в  том, что  решение  находится  путем  геометрических построений. Например,  для  нахождения  корней  уравнения  f (х) = 0  строится  график  функции                  y = f(х), точки  пересечения которого с  осью  абсцисс и будут  искомыми  корнями.

При  использовании  аналитических  методов решение  задачи  удается  выразить  с  помощью  формул. В частности, если  математическая  задача  состоит  в  решении  простейших  алгебраических или  трансцендентных  уравнений, дифференциальных  уравнений и т.п., то  использование  известных  из  курса  математики  приемов  сразу  приводит  к цели.  К  сожалению,  на  практике  это  слишком  редкие  случаи.

Основным  инструментом  для  решения  сложных  математических  задач  в настоящее  время  являются  численные  методы, позволяющие  свести решение  задач  к  выполнению  конечного  числа  арифметических  действий  над  числами; при  этом  результаты  получаются  в виде числовых  значений. Многие  численные  методы  разработаны  давно, однако  при  вычислениях  вручную они  могли  использоваться лишь  для  решения  не  слишком  трудоемких  задач.    

С  появлением  ЭВМ  начался  период  бурного  развития  численных  методов  и  их  внедрения  в  практику. Только  вычислительной  технике  под  силу  выполнить  за  сравнительно  короткое  время  объем  вычислений  в  миллионы, миллиарды  и  более  операций,  необходимых  для  решения  многих  современных  задач. При  счете  вручную человеку  не  хватило  бы  и  жизни  для решения  одной  такой  задачи.

Численный  метод  наряду  с  возможностью  получения  результата  за  приемлемое  время   должен  обладать  и  еще  одним  важным  качеством – не  вносить  в  вычислительный  процесс  значительных  погрешностей.                 

1.Нахождение действительных корней нелинейных и трансцендентных  уравнений.

Задача  нахождения  корней  нелинейных  уравнений  вида

F (х) = 0        (1.1)

встречается  в  различных  областях  научных  исследований (здесь F (х) -  некоторая  непрерывная  функция.)  Нелинейные  уравнения  можно  разделить  на  два  класса   - алгебраические  и трансцендентные.  Алгебраическими    уравнениями  называются  уравнения,  содержащие  только  алгебраические  функции (целые, рациональные, иррациональные). В частности,  многочлен  является  целой алгебраической  функцией. Уравнения, содержащие   другие  функции  (тригонометрические,  показательные,  логарифмические  и  другие),  называются  трансцендентными.

Общий  вид  алгебраического  уравнения

      (1.2)

При  этом  будем  считать, что  функция  f(x)  определена  и  непрерывна  в  некотором  интервале  (a,b).  Всякое  значение  х, обращающее функцию  в нуль, называется корнем  уравнения .

Приближенное  нахождение  действительных  корней  уравнения  состоит  из  двух  этапов:

1.отделение  корней, т.е. установление  промежутков, в которых  содержится  только  один  корень  уравнения;

2.Оценка  точности  определения, т.е. погрешности, на  сколько найденное  значение  корня  отличается  от  истинного.

1.1.  Метод решения ( Метод  хорд).

В основе  этого  метода  лежит  линейная  интерполяция  заданной  функции  по  двум  значениям, имеющим  противоположные  знаки.

Определяются  значения  функций  в  правой  и левой  границах  выбранного интервала. Затем эти  две  точки  соединяются  прямой  линией (хордой).  Эта  прямая  пересекает  ось  абсцисс в  точке  с  координатами.

            (1.1.1)                      

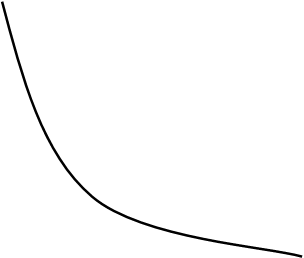
После  этого  находят  значение функции в  точке х = х^* и сравнивают  его со  знаком функции  на  концах  исходного  интервала. Затем  используют  f (х^*)  вместо  того  значения,  с которым  оно  совпадает  по  знаку.  Итерационный  процесс  продолжается  до  тех  пор, пока  не  будет  достигнута  заданная  точность  определения  корня.  Графическая интерпретация  метода  хорд представлена  на  рисункее  1.1.1

Рис.1.1.1. Интерпретация  метода хорд.

Пусть  мы  нашли  отрезок  [a,b], на  котором  функция  F (х)  меняет  знак.  Для  определенности примем F(а) < 0,  F (b)> 0 ( рис.1.1.1). В данном  методе  процесс  итераций  состоит  в  том , что  в  качестве  приближений  к  корню  уравнения  (1.1)  принимаются  значения  х* , х₁, ... х_п точек  пересечения  хорды  с  осью  абсцисс.

Сначала  находим  уравнения  хорды АВ: